Straightedge and compass construction

Original article: w:Straightedge and compass construction

"Constructive geometry" redirects here. It is not to be confused with Constructive solid geometry.

Creating a regular hexagon with a straightedge and compass

직선자와 컴퍼스 구성(Straightedge and compass construction)은, 역시 자-와-컴퍼스 구성(ruler-and-compass construction) 또는 고전적 구성(classical construction)으로 알려져 있으며, 오직 이상화된(idealized) 자(ruler)와 한 쌍의 컴퍼스(compass)를 사용하여 길이, 각도(angle), 및 다른 기하학적 도형을 구성하는 것입니다.

이상화된 자는, 직선자(straightedge)로 알려져 있으며, 길이에서 무한이고, 오직 하나의 가장자리를 가지고, 그것 위에 표시가 없는 것으로 가정됩니다. 컴퍼스는 최대 또는 최소 반지름을 가지지 않음으로 가정되고, 종이에서 들어올릴 때 "접히는" 것으로 가정하므로, 거리를 옮기기 위해 직접 사용되지 않을 수 있습니다. (이것은 중요하지 않은 제약인데, 왜냐하면, 여러-단계 절차를 사용하여, 거리는 접히는 컴퍼스라도 전송될 수 있기 때문입니다; 컴퍼스 동치 정리(compass equivalence theorem)를 참조하십시오. 어쨌든, 직선자를 대고 있는 접히지 않는 컴퍼스는 그것을 표시하는 것과 동등한 것처럼 보일 수 있지만, 뉴시스 구성(neusis construction)은 여전히 허용될 수 없고 이것이 표시되지 않은 것이 실제로 의미하는 것임을 주목하십시오: 아래의 표시-가능 자(Markable rulers)를 참조하십시오.) 보다 형식적으로, 유일한 허용-가능 구성은 유클리드(Euclid)의 처음 세 가지 공준(postulates)에 의해 부여된 구성입니다.

직선자와 컴퍼스를 사용하여 구성-가능한 모든 각 점은 역시 컴퍼스 단독으로 사용하여 구성될 수 있거나, 단일 원과 그 중심이 주어지면 직선자 단독에 의해 구성될 수 있는 경우임이 밝혀졌습니다.

고대 그리스 수학자들(ancient Greek mathematicians)은 처음으로 직선자와 컴퍼스 구성을 생각했었고, 평면 기하학(plane geometry)에서 많은 고대 문제가 이러한 제한을 부과합니다. 고대 그리스인들은 많은 구성을 개발했지만, 일부 경우에서 그렇게 하는 것이 불가능했습니다. 가우스(Gauss)는 일부 다각형(polygon)은 구성할 수 있지만 대부분은 그렇지 않음을 보여주었습니다. 가장 유명한 직선자와 컴퍼스 문제 중 일부는 1837년 피에르 완젤(Pierre Wantzel)에 의해 필드의 수학적 이론을 사용하여 불가능하다는 것이 입증되었습니다.

기존의 불가능성의 증명(proofs of impossibility)에도 불구하고, 일부는 이러한 문제를 해결하기 위해 계속 노력하고 있습니다. 이들 문제의 대부분은 다른 기하학적 변환이 허용된다면 가정하면 쉽게 해결될 수 있습니다: 예를 들어, 정육면체를 두 배(doubling the cube)는 기하학적 구성을 사용하여 가능하지만, 직선자와 컴퍼스 단독으로 사용하여 불가능합니다.

대수학(algebra)의 관점에서, 하나의 길이가 구성-가능인 것과 그것이 구성-가능 숫자(constructible number)를 나타내는 것은 필요충분(iff) 조건이고, 하나의 각도가 구성-가능인 것과 그것의 코사인(cosine)이 구성-가능 숫자인 것은 필요충분 조건입니다. 하나의 숫자는 구성-가능인 것과 그것이 넷의 기본 산술 연산과 제곱근(square root) 추출을 사용하여 쓸 수 있지만 고차근은 사용할 수 없는 것은 필요충분 조건입니다.

Straightedge and compass tools

Straightedge and compass

A compass

직선자와 컴퍼스 구성의 "직선자"와 "컴퍼스"는 실제 세계에서 눈금자와 컴퍼스의 이상화입니다:

• 직선자는 무한하게 길지만, 그것은 그것 위에 표시를 가지지 않고 보통의 자와 달리 오직 하나의 똑바른 가장자리를 가집니다. 그려진 직선은 무한소적으로 얇은 점-너비입니다. 그것은 오직 두 점 사이에 무한 정밀도로 선분을 그리거나, 기존 선분을 확장하기 위해 사용될 수 있습니다.
• 컴퍼스는 임의적인 너비로 벌릴 수 있지만, (일부 실제 컴퍼스와 달리) 그것 위에 표시를 가지지 않습니다. 원은 오직 둘의 주어진 점: 중심과 원의 한 점에서 시작하여 무한 정밀도로 해당 점에 맞춰 그려질 수 있습니다. 그려진 호는 무한소적으로 얇은 점-너비입니다. 컴퍼스는 원이 그려지지 않을 때 접힐 수도 있고 접히지 않을 수도 있습니다.

실제 컴퍼스는 접히지 않고 현대 기하학적 구성은 종종 이 특색을 사용합니다. '접히는 컴퍼스'는 덜 강력한 도구로 보일 것입니다. 어쨌든, 유클리드의 원론(Euclid's Elements) 제 1권 제안 2에서 컴퍼스 동치 정리에 의해, 강력함은 접히는 컴퍼스를 사용함으로써 손실되지는 않습니다. 비록 그 제안이 정확할지라도, 그것의 증명은 길고도 신뢰할 수 없는 역사를 가지고 있습니다. 임의의 경우에서, 동치는 이상적인 컴퍼스의 정의에 이 특색이 규정되지 않은 이유입니다.

각 구성은 정확해야 합니다. 그것을 "눈으로 확인"하고 (필수적으로 구성을 보고 그것의 정확도를 추측하거나, 자 위의 측정의 단위와 같은 측정의 형식을 사용) 가까이 가는 것은 해결책으로 고려되지 않습니다.

각 구성은 종료되어야 합니다. 즉, 그것은 유한 단계의 숫자를 가져야 하고, 더 가까운 근사의 극한이 아니어야 합니다.

이런 식으로 말하면, 직선자와 컴퍼스 구성은 심각한 실제 문제라기 보다는 휴게실 게임(parlour game)처럼 보입니다; 그러나 제한의 목적은 구성이 정확하게 올바른 것으로 입증될 수 있음을 보장하는 것입니다.

History

고대 그리스 수학자들(ancient Greek mathematicians)은 먼저 직선자와 컴퍼스 구성을 시도했었고, 그들은 주어진 길이의 합(sums), 차이(differences), 곱(products), 비율(ratio), 및 제곱근(square root)을 구성하는 방법을 발견했습니다. 그들은 역시 주어진 각의 절반, 그것의 넓이가 다른 정사각형의 두 배인 정사각형, 주어진 다각형과 같은 넓이를 갖는 정사각형, 3, 4, 또는 5 변을 갖는 정규 다각형 (또는 주어진 다각형의 변의 두 배 숫자를 갖는 다각형)을 구성할 수 있습니다. 그러나 그들은 특별한 경우를 제외하고는 주어진 각도의 삼분의 일, 또는 주어진 원과 같은 넓이를 갖는 정사각형, 또는 변의 다른 숫자를 갖는 정규 다각형을 구성할 수 없었습니다. 그들은 주어진 변을 가진 정육면체의 부피 두 배인 정육면체의 한 변도 만들 수 없습니다.

히포크라테스(Hippocrates)와 메나이크모스(Menaechmus)는 정육면체의 부피는 쌍곡선(hyperbola)과 포물선(parabola)의 교점을 찾음으로써 두 배가 될 수 있지만, 이것들은 직선자와 컴퍼스로는 구성될 수 없음을 보여주었습니다. 기원전 5세기에, 히피아스(Hippias)는 일반적인 각도를 삼등분하고 원을 정사각형화하기 위해 구적선(quadratrix)이라고 불리는 곡선을 사용했었고, 기원전 2세기에 니코메데스(Nicomedes)는 콘코이드(conchoid)를 사용하여 임의적인 각도를 삼등분하는 방법을 보여주었습니다; 그러나 이들 방법들은 역시 단지 직선자와 컴퍼스로는 따를 수 없습니다.

1796년 가우스(Gauss)가 17 변을 가진 정규 다각형이 구성될 수 있음을 보여줄 때까지, 이천년 동안 미해결 문제에 대한 진전이 없었습니다; 5년 후 그는 n 변의 정규 다각형을 구성할 수 있는 충분 기준을 보여주었습니다.

1837년 피에르 완젤(Pierre Wantzel)은 길이의 세제곱근(cube root)을 구성하는 것의 불가능성을 기반으로 임의적인 각도를 삼등분하거나 정육면체의 부피를 두 배로 하는 것의 불가능성의 증명을 발표했습니다. 그는 역시 정규 다각형에 대해 가우스의 충분 구성가능성 조건이 역시 필요임을 보여주었습니다.

그런-다음 1882년 린데만(Lindemann)은 $\pi$가 초월적 숫자(transcendental number)이고, 따라서 직선자와 컴퍼스로 주어진 원과 같은 넓이를 정사각형을 구성하는 것이 불가능하다는 것을 보여주었습니다.

The basic constructions

The basic constructions

모든 직선자와 컴퍼스 구성은 이미 구성된 점, 직선 및 원을 사용하여 5가지 기본 구성을 반복적으로 적용하는 것으로 구성됩니다. 이것들은 다음입니다:

• 둘의 기존 점을 통해 직선 만들기
• 한 점을 중심으로 또 다른 점을 통한 원 만들기
• 둘의 기존의 평행하지 않은 직선의 교차점인 점 만들기
• (만약 그것들이 교차하면) 직선과 원의 교차점에서 하나 또는 둘의 점 만들기
• (만약 그것들이 교차하면) 두 원의 교차점에 하나 또는 둘의 점 만들기.

예를 들어, 단지 둘의 구별되는 점으로 시작하여, 우리는 직선 또는 둘의 원 중 하나를 만들 수 있습니다 (차례로, 각 점을 중심으로 사용하고 다른 점을 통과해서 만들 수 있습니다). 만약 우리가 두 원을 모두 그리면, 둘의 새로운 점이 그것들의 교차점에서 생성됩니다. 둘의 원래 점과 이들 새로운 점 중 하나 사이에 직선을 그리면 등변 삼각형의 구성을 완성합니다.

그러므로, 임의의 기하학적 문제에서, 우리는 초기 기호의 집합 (점과 직선), 알고리듬, 및 일부 결과를 가집니다. 이러한 관점에서, 기하학은 그것의 원소를 기호로 대체하는 공리적 대수(algebra)와 동등합니다. 아마도 가우스(Gauss)는 이것을 처음 깨닫고, 그것을 일부 구성의 불가능성을 입증하기 위해 사용했을 것입니다; 훨씬 후에 힐베르트(Hilbert)는 기하학에 대해 완전한 공리의 집합을 찾았습니다.

Much used straightedge and compass constructions

가장 많이 사용되는 직선자와 컴퍼스 구성은 다음을 포함합니다:

• 선분에서 수직 이등분선 만들기
• 선분의 중간점 찾기
• 한 점에서 한 직선까지 수직 직선 그리기
• 각도 이등분하기
• 한 직선에서 한 점 미러링
• 원에 접하는 점을 통과하는 직선 구성하기
• 3 비-공선형 점을 통과하는 원 구성하기
• 주어진 직선에 평행한 주어진 점을 지나는 직선을 그리기

Constructible points

Main article: Constructible number

대수적 연산에 해당하는 직선자와 컴퍼스 구성
x=a·b   (intercept theorem)	x=a/b   (intercept theorem)	x=√a   (Pythagorean theorem)

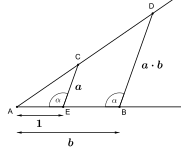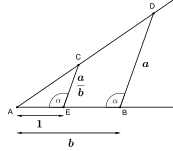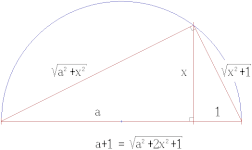우리는 두 직선으로 구성된 데카르트 좌표 시스템(Cartesian coordinate system)을 사용하여 대수학을 기하학에 결합하고, 평면의 점을 벡터(vector)로 나타낼 수 있습니다. 마지막으로 우리는 이들 벡터를 복소수로 쓸 수 있습니다.

직선과 원에 대해 방정식을 사용하여, 우리는 그것들이 교차하는 점이 직선 위의 두 점, 원의 중심, 및 원의 반지름을 포함하는 가장 작은 필드 F의 이차 확장(quadratic extension)에 놓임을 보일 수 있습니다. 즉, 그것들은 형식 x +y√k의 것이며, 여기서 x, y, 및 k는 F에 있습니다.

구성-가능 점의 필드는 제곱근 아래에서 닫혀 있기 때문에, 그것은 유리 계수를 갖는 복소수 필드의 유한 수열 이차 확장에 의해 얻어질 수 있는 모든 점을 포함합니다. 위의 단락을 통해, 우리는 임의의 구성-가능 점이 그러한 확장의 수열로 얻어질 수 있음을 보일 수 있습니다. 이것의 결과로, 우리는 구성-가능 점 (및 따라서 임의의 구성-가능한 길이)에 대해 최소 다항식의 차수가 2의 거듭제곱이라는 것을 찾습니다. 특히, 임의의 구성-가능 점 (또는 길이)은, 비록 모든 각 대수적 숫자(algebraic number)가 구성-가능은 아닐지라도, 대수적 숫자입니다; 예를 들어, ³√2는 대수적이지만 구성-가능은 아닙니다.

Constructible angles

구성-가능인 각도와 임의의 구성-가능 원 위에 구성-가능인 점 사이에는 전단사(bijection)가 있습니다. 구성-가능인 각도는 덧셈 모듈로 2π 아래에서 아벨 그룹(abelian group)을 형성합니다 (이것은 복소수로 여겨지는 단위 원 위의 점의 곱셈에 해당합니다). 구성-가능인 각도는 정확하게 그것의 탄젠트 (또는 동등하게 사인 또는 코사인)가 숫자로 구성-가능인 각도입니다. 예를 들어, 정규 십칠각형(heptadecagon) (열일곱-변 정규 다각형(regular polygon))은 다음과 같은 이유로 구성-가능입니다:

$\cos {\left({\frac {2\pi }{17}}\right)}=-{\frac {1}{16}}\;+\;{\frac {1}{16}}{\sqrt {17}}\;+\;{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\;+\;{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}$

이것은 가우스(Gauss)에 의해 발견되었습니다.

구성-가능 각도의 그룹은 각도를 절반으로 나누는 연산 아래에 닫혀 있습니다 (이것은 복소수에서 제곱근을 취하는 것에 해당합니다). 두 점으로 시작하여 구성될 수 있는 유한 차수의 유일한 각도는 그것의 차수가 이의 거듭제곱이거나, 이의 거듭제곱과 구별되는 페르마 소수(Fermat primes) 집합의 곱인 각도입니다. 게다가 무한 차수의 구성-가능 각도의 조밀한 집합이 있습니다.

Relation to complex arithmetic

유클리드 평면(Euclidean plane)에서 점 집합이 주어지면, 임의적인 방향(orientation)의 선택과 함께 그것들 중 임의의 하나를 0이라고 하고 또 다른 하나를 1이라고 하는 것을 선택하면 점을 복소수(complex number)의 집합으로 고려하는 것을 허용합니다.

점의 집합을 복소수로의 임의의 그러한 해석이 주어지면, 유효한 직선자와 컴퍼스 구성 단독으로 사용하여 구성할 수 있는 점은 정확하게 원래 점의 집합을 포함하고 복소 켤레(complex conjugate)와 제곱근(square root) 연산 아래에서 닫혀 있는 가장 작은 필드(field)의 원소입니다 (모호성 피하기 위해, 우리는 π보다 작은 복소수 편각(complex argument)으로 제곱근을 지정할 수 있습니다). 이 필드의 원소는 정확하게 덧셈(addition), 뺄셈(subtraction), 곱셈(multiplication), 나눗셈(division), 복소 켤레(complex conjugate), 및 제곱근(square root)의 연산을 오직 사용하여 원래 점에서 공식으로 표현될 수 있는 원소이며, 이것은 평면의 셀-수-있는 조밀한 부분집합임을 쉽게 보일 수 있습니다. 이들 여섯 연산은 각각 간단한 직선자와 컴퍼스 구성에 해당합니다. 그러한 공식에서 각 산술 연산에 대해 구성을 조합함으로써 해당하는 점의 구성을 생성하는 것은 간단합니다. 특정 접의 집합의 보다 효율적인 구성은 그러한 계산에서 지름길에 해당합니다.

동등하게 (및 임의적으로 두 점을 선택할 필요없이) 우리는 임의적인 방향의 선택이 주어지면, 점의 집합이 임의의 두 쌍의 점 사이의 차이의 비율로 주어진 복소수 비율의 집합을 결정한다고 말할 수 있습니다. 그러한 비율의 집합에서 직선자와 컴퍼스를 사용하여 구성-가능 비율의 집합은 원래 비율을 포함하는 가장 작은 필드이고 복소 켤레와 제곱근을 취하는 것 아래에서 닫혀 있습니다.

예를 들어, 실수 부분, 허수 부분, 및 점 또는 비율 z의 모듈러스 (위의 두 가지 관점 중 하나를 취함)는 다음으로 표현될 수 있으므로 구성-가능입니다:

$\mathrm {Re} (z)={\frac {z+{\bar {z}}}{2}}\;$

$\mathrm {Im} (z)={\frac {z-{\bar {z}}}{2i}}\;$

$\left|z\right|={\sqrt {z{\bar {z}}}}.\;$

정육면체를 두 배하는 것 및 각도의 삼등분 (φ/2π가 분모(denominator)가 3으로 나누어지지 않는 유리수(rational number)임을 만족하는 임의의 φ와 같은 특수 각도를 제외)은 삼차 방정식(cubic equation)의 해인 비율을 요구하지만, 원을 정사각형화는 초월적(transcendental) 비율을 요구합니다. 이들 중 어느 것도 설명된 필드에 있지 않으므로, 이것들에 대해 직선자와 컴퍼스 구성이 존재하지 않습니다.

Impossible constructions

고대 그리스인들은 그들이 해결할 수 없는 구성 문제가 단순히 완고한 것이지 해결할 수 없는 것이 아니라고 생각했습니다. 현대적인 방법과 함께, 어쨌든, 이들 직선자와 컴퍼스 구성은 수행하는 것이 논리적으로 불가능한 것으로 보여 왔습니다. (문제 자체는, 어쨌든, 해결할 수 있고, 그리스인은 오직 직선자와 컴퍼스로 작업해야 한다는 제약없이 문제를 해결하는 방법을 알고 있었습니다.)

Squaring the circle

Main article: Squaring the circle

이들 문제 중 가장 유명한 문제, 원을 정사각형화(squaring the circle)는, 그렇지 않으면 원의 구적법으로 알려져 있으며, 오직 직선자와 컴퍼스를 사용하여 주어진 원과 같은 넓이를 갖는 정사각형을 구성하는 문제입니다.

원을 정사각형화하는 것은 초월적 숫자(transcendental number), 즉, √π를 생성하는 것을 포함하기 때문에 불가능한 것으로 입증되어 왔습니다. 오직 특정 대수적 숫자(algebraic number)가 자와 컴퍼스 단독으로 구성될 수 있으며, 즉, 덧셈, 뺄셈, 곱셈, 나눗셈, 및 제곱근을 취하는 것의 유한 연산의 수열로 정수로부터 구성된 숫자입니다. 이러한 이유로 "원을 정사각형화"라는 문구는 종종 "불가능한 일을 하는 것"을 의미하기 위해 사용됩니다.

자와 컴퍼스 단독으로 해를 요구하는 제약없이, 그 문제는 다양한 기하학적 및 대수적 수단으로 쉽게 해결할 수 있고, 고대에 여러 번 해결되었습니다.

케플러 삼각형(Kepler triangle)을 사용하여 "원의 구적법"에 매우 근사적으로 매우 가깝게 되는 방법은 달성될 수 있습니다.

Doubling the cube

Main article: Doubling the cube

정육면체를 두 배로 늘리는 것은 오직 직선-자와 컴퍼스를 사용하여 주어진 가장자리를 갖는 정육면체의 두 배 부피를 가지는 정육면체의 가장자리의 구성입니다. 이것은 불가능한데 왜냐하면 2의 세제곱근은 비록 대수적이지만 덧셈, 뺄셈, 곱셈, 나눗셈, 및 제곱근을 취함으로써 정수에서 계산될 수 없기 때문입니다. 이것은 유리수에 걸쳐 최소 다항식(minimal polynomial)이 차수 3을 가지기 때문입니다. 이 구성은 그것 위에 둘의 표시를 갖는 직선자와 컴퍼스를 사용하여 가능합니다.

Angle trisection

Main article: Angle trisection

각도 삼등분은 오직 직선자와 컴퍼스를 사용하여 주어진 임의적인 각도의 삼분의 일인 각도의 구성입니다. 이것은 일반적인 경우에는 불가능합니다. 예를 들어, 각도 2π/5 라디안(radian) (72° = 360°/5)은 삼등분될 수 있지만, π/3 라디안 (60°)의 각도는 삼등분될 수 없습니다. 일반적인 삼등분 문제는 역시 둘의 표시를 갖는 직선자가 허용될 때 (뉴시스(neusis) 구성) 쉽게 해결됩니다.

Distance to an ellipse

평면에서 임의의 점에서 원(circle) 위의 가장 가까운 점까지의 선분은 구성될 수 있지만, 평면에서 임의의 점에서 양의 이심률(eccentricity)을 갖는 타원(ellipse)의 가장 가까운 점까지의 선분은 일반적으로 구성될 수 없습니다.

Alhazen's problem

1997년, 옥스포드(Oxford) 수학자 피터 노이만(Peter M. Neumann)은 고대 알하겐의 문제(Alhazen's problem) (당구 문제 또는 구형 거울로부터 반사)의 일반적인 해결책에 대해 자-와-컴퍼스 구성이 없다는 정리를 입증했습니다.

Constructing regular polygons

Main article: Constructible polygon

Construction of a regular pentagon

일부 정규 다각형(regular polygon) (예를 들어, 오각형(pentagon))은 직선자와 컴퍼스로 구성하는 것이 쉽습니다; 다른 것들은 그렇지 않습니다. 이것은 다음 질문으로 이어졌습니다: 직선자와 컴퍼스를 사용하여 모든 정규 다각형을 구성할 수 있습니까?

1796년 카를 프리드리히 가우스(Carl Friedrich Gauss)는 정규 17-변 다각형이 구성될 수 있음을 보여주었고, 오년 후에 정규 n-변 다각형이 만약 n의 홀수 소수 인수(prime factor)가 구별되는 페르마 소수(Fermat prime)이면 직선자와 컴퍼스로 구성될 수 있음을 보여주었습니다. 가우스는 이 조건도 필요(necessary)라고 추측(conjecture)했지만, 그는 이 사실의 증명을 제공하지 않았으며, 이것은 1837년 피에르 완젤(Pierre Wantzel)에 의해 제공되었습니다.

처음 몇 개의 구성-가능 정규 다각형은 다음 숫의 변을 가집니다:

3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272... (OEIS에서 수열 A003401)

짝수의 변을 갖는 구성-가능 정규 다각형의 무한대가 있는 것으로 알려져 있습니다 (왜냐하면 만약 정규 n-각형이 구성-가능이면, 정규 2n-각형도 구성-가능이고 따라서 정규 4n-각형, 8n-각형 등도 구성가능이기 때문입니다). 어쨌든, 홀수의 변을 갖는 구성-가능 정규 n-각형은 오직 31개로 알려져 있습니다.

Constructing a triangle from three given characteristic points or lengths

삼각형(triangle)의 열여섯 핵심 점은 꼭짓점(vertices), 변의 중간점, 고도(altitudes)의 발, 내부 각도 이등분선의 발, 및 둘레중심(circumcenter), 도형중심(centroid), 직교중심(orthocenter)과 내중심(incenter)입니다. 이것들은 한 번에 셋을 취하여 셋의 점에서 삼각형을 구성하는 139개의 구별되는 비-자명한 문제를 산출할 수 있습니다. 이러한 문제 중, 셋은 다른 두 점에서 고유하게 구성될 수 있는 한 점과 관련이 있습니다; 23은 (사실 무한하게 많은 해에 대해) 비-고유하게 구성될 수 있지만 점들의 위치가 특정 제약 조건을 따르는 경우에만 가능합니다. 74에서 그 문제는 일반적인 경우에서 구성-가능입니다; 그리고 39에서 요구된 삼각형이 존재하지만 구성-가능은 아닙니다.

삼각형의 열둘의 주요 길이는 셋의 변의 길이, 셋의 고도(altitudes), 셋의 중앙선(medians), 및 셋의 각도 이등분선(angle bisectors)입니다. 세 각과 함께, 이것들은 95개 구별되는 조합을 제공하고, 그 중 63개는 구성-가능 삼각형을 생성하고, 그 중 30개는 그렇지 않고, 그 중 둘은 정의되지 않습니다.

Restricted Constructions

다양한 시도가 컴퍼스와 직선자가 할 수 있는 모든 것을 구성할 수 있는 데 필요한 최소 기준을 결정할 뿐만 아니라, 무엇이 여전히 구성-가능인지와 그것이 구성될 수 있는 방법을 결정하기 위해 다양한 규칙 아래에서 구성에 대해 허용 가능한 도구를 제한하기 위해 만들어져 왔습니다.

Constructing with only ruler or only compass

모르–마스케로니 정리(Mohr-Mascheroni theorem)에 따르면, 주어진 데이터와 찾으려는 데이터가 (직선이나 원이 아닌) 이산 점으로 구성된다는 조건 아래에서 자와 컴퍼스로 구성될 수 있으면 단지 컴퍼스로 무엇이든 구성할 수 있습니다. 이 정리의 진리는 아르키메데스의 공리(Archimedes' axiom)의 진리에 의존하며, 이것은 자연에서 일-차가 아닙니다. 컴퍼스-단독 구성의 예제는 나폴레옹의 문제(Napoleon's problem)를 포함합니다.

단지 자로 제곱근을 구하는 것은 불가능하므로, 자로 구성될 수 없는 일부의 것은 컴퍼스로 구성될 수 있습니다; 그러나 (퐁슬레–슈타이너 정리(Poncelet–Steiner theorem)에 의해) 단일 원과 그 중심이 주어지면, 그것들은 구성될 수 있습니다.

Extended constructions

고대 그리스인들은 그것들의 해에 요구된 도구의 복잡성에 따라 구성을 세 가지 주요 카테고리로 분류했습니다. 만약 구성이 오직 직선자와 컴퍼스를 사용했으면, 그것은 평면이라고 불렀습니다; 만약 그것이 역시 하나 이상의 원뿔 단면 (원 제외)을 요구했으면, 그것은 고체라고 불렀습니다; 세 번째 카테고리는 다른 두 카테고리에 속하지 않는 모든 구성을 포함했었습니다. 이 분류는 현대 대수적 관점과 잘 맞습니다. (위에서 설명한 대로) 오직 필드 연산과 제곱근을 사용하여 표현될 수 있는 복소수는 평면 구성을 가집니다. 세제곱근의 추출도 포함하는 복소수는 고체 구성을 가집니다.

필드의 언어에서, 평면인 복소수는 2의 거듭제곱 차수를 가지고, 각 확장이 차수 2를 가지는 필드의 타워로 분해될 수 있는 필드 확장(field extension)에 놓입니다. 고체 구성을 가지는 복소수는 오직 이와 삼의 소수 인수를 갖는 차수를 가지고, 각 확장이 차수 2 또는 3을 가지는 필드의 타워의 맨 위에 있는 필드 확장에 놓입니다.

Solid constructions

한 점은 만약 직선자, 컴퍼스, 및 이미 구성된 초점, 방향선, 및 이심률을 갖는 임의의 원뿔형을 그릴 수 있는 (아마도 가상의) 원뿔형 그리기 도구를 사용하여 구성될 수 있으면 고체 구성입니다. 같은 한 점의 집합은 종종 더 작은 도구의 집합을 사용하여 구성될 수 있습니다. 예를 들어, 컴퍼스, 직선자, 및 점 (0,0)과 (1,0)과 함께 포물선 y=x²를 가지는 종이를 사용하여, 우리는 고체 구성을 가지는 임의의 복소수를 구성할 수 있습니다. 마찬가지로, 이미 구성된 초점과 주요 축 (2개의 핀과 한 개의 끈)을 갖는 임의의 타원을 그릴 수 있는 도구는 마찬가지로 강력합니다.

고대 그리스인들은 정육면체를 두 배하는 것과 임의적인 각도를 삼등분하는 것이 모두 고체 구성을 가진다는 것을 알고 있었습니다. 아르키메데스는 정규 7-각형의 고체 구성을 제공했습니다. 원의 구적법은 고체 구성을 가지지 않습니다.

정규 n-각형이 고체 구성을 가지는 것과 n=2^j3^km인 것은 필요충분 조건이며 여기서 m은 구별되는 피어폰트 소수(Pierpont prime) (형식 2^r3^s+1의 소수)의 곱입니다. 그러한 n의 집합은 다음 수열입니다:

7, 9, 13, 14, 18, 19, 21, 26, 27, 28, 35, 36, 37, 38, 39, 42, 45, 52, 54, 56, 57, 63, 65, 70, 72, 73, 74, 76, 78, 81, 84, 90, 91, 95, 97... (OEIS에서 수열 A051913)

정규 n-각형이 고체 구성을 가지지 않는 n의 집합은 다음 수열입니다:

11, 22, 23, 25, 29, 31, 33, 41, 43, 44, 46, 47, 49, 50, 53, 55, 58, 59, 61, 62, 66, 67, 69, 71, 75, 77, 79, 82, 83, 86, 87, 88, 89, 92, 93, 94, 98, 99, 100... (OEIS에서 수열 A048136)

페르마 소수에 대한 질문과 마찬가지로, 피어폰트 소수의 무한 숫자가 있는지 여부는 열린 질문입니다.

Angle trisection

직선자와 컴퍼스와 함께, 우리가 임의적인 각도를 (오직) 삼등분할 수 있는 도구가 있다면 어떨까요? 그러한 구성은 고체 구성이지만 그러한 도구를 사용하여 구성될 수 없는 고체 구성을 갖는 숫자가 있습니다. 예를 들어, 우리는 그러한 도구로 정육면체를 두 배로 늘릴 수 없습니다. 다른 한편으로, 고체 구성을 가지는 모든 각 정규 n-각형은 그러한 도구를 사용하여 구성될 수 있습니다.

Origami

Main article: Huzita–Hatori axioms

종이접기의 수학적 이론은 직선자와 컴퍼스 구성보다 더 강력합니다. 후지타–하토리(Huzita–Hatori) 공리를 만족시키는 접기는 컴퍼스와 원뿔형 그리기 도구를 사용하여 확장된 구성과 정확히 같은 점의 집합을 구성할 수 있습니다. 그러므로, 오리가미(origami)는 역시 삼차 방정식 (및 따라서 사차 방정식)을 풀기 위해 사용될 수 있고, 따라서 두 가지 고전적인 문제를 해결할 수 있습니다.

Markable rulers

Main article: Neusis construction

아르키메데스(Archimedes), 니코메데스(Nicomedes), 및 아폴로니우스(Apollonius)는 표시-가능한 자의 사용을 포함하는 구성을 제공했습니다. 이것은 예를 들어 선분, 둘의 직선 (또는 원), 및 한 점을 취하는 것을 허용할 것입니다; 그리고 그때에 주어진 점을 통과하고 교차점 사이의 거리가 주어진 선분과 같음을 만족하는 둘의 주어진 직선을 교차하는 직선을 그리십시오. 이것은 그리스인들에게 뉴시스(neusis) ("inclination", "tendency" 또는 "verging")라고 불렸는데, 왜냐하면 새로운 직선이 점을 향하는 경향이 있기 때문입니다. 이 확장된 방식에서, 우리는 임의적인 각도를 삼등분 (아르키메데스의 삼등분을 참조)하거나 (니코메데스로 인해) 임의적인 세제곱근을 추출할 수 있습니다. 그러므로, 기존 거리에 대한 비율이 삼차(cubic) 또는 사차 방정식(quartic equation)의 해인 임의의 거리는 구성-가능입니다. 표시-가능한 자를 사용하여, 칠각형과 같은 고체 구성을 갖는 정규 다각형은 구성-가능입니다; 그리고 존 콘웨이(John H. Conway)와 리처드 가이(Richard K. Guy)는 그들 중 몇몇에 대해 구성을 제공합니다.

뉴시스 구성은 원뿔형 그리기 도구보다 강력한데, 왜냐하면 우리는 고체 구성을 가지지 않는 복소수를 구성할 수 있기 때문입니다. 사실, 이 도구를 사용하여, 우리는 제곱근을 사용하여 해결할 수 없는 일부 오차 방정식을 해결할 수 있습니다. 우리는 7보다 크거나 같은 소수 차수의 기약 다항식을 뉴시스 구성을 사용하여 풀 수 없음을 알고 있으므로, 이 도구를 사용하여 정규 23-각형 또는 29-각형을 구성하는 것은 가능하지 않습니다. 벤저민(Benjamin)과 스나이더(Snyder)는 정규 11-각형을 구성하는 것이 가능하다는 것을 입증했지만, 구성을 제공하지는 않았습니다. 정규 25-각형 또는 31-각형이 이 도구를 사용하여 구성-가능인지 여부는 아직 열려 있습니다.

Computation of binary digits

1998년 시몽 플루페(Simon Plouffe)는 특정 숫자의 이진 자릿수(binary digit)를 계산하기 위해 사용될 수 있는 자와 컴퍼스 알고리듬(algorithm)을 제공했습니다. 그 알고리듬은 각도의 반복적인 두 배를 포함하고 약 20개의 이진 자릿수 후에는 물리적으로 비실용적이 됩니다.

See also

• Carlyle circle
• Geometric cryptography
• Geometrography
• List of interactive geometry software, most of them show straightedge and compass constructions
• Mathematics of paper folding
• Underwood Dudley, a mathematician who has made a sideline of collecting false straightedge and compass proofs.

External links

• Regular polygon constructions by Dr. Math at The Math Forum @ Drexel
• Construction with the Compass Only at cut-the-knot
• Angle Trisection by Hippocrates at cut-the-knot
• Weisstein, Eric W. "Angle Trisection". MathWorld.