Differential calculus

Original article: w:Differential calculus

The graph of a function, drawn in black, and a tangent line to that function, drawn in red. The slope of the tangent line equals the derivative of the function at the marked point.

수학(mathematics)에서, 미분 미적분학(differential calculus)은 양이 변하는 비율의 연구와 관련된 미적분학(calculus)의 하위-분야입니다. 그것은 미적분학의 두 가지 전통적인 분야 중 하나이며, 나머지 하나는 적분 미적분학(integral calculus), 곡선 아래 넓이의 연구입니다.

미분 미적분에서 연구의 주요 대상은 함수(function)의 도함수(derivative), 미분(differential)과 같은 관련된 개념, 및 그의 응용입니다. 선택된 입력 값에서 함수의 도함수는 그 입력 값 근처에서 함수의 변화율을 묘사합니다. 도함수를 찾는 과정은 미분화(differentiation)로 불립니다. 기하학적으로, 한 점에서의 도함수는 해당 점에서 함수의 그래프(graph of the function)에 대한 접선(tangent line)의 기울기(slope)이며, 도함수가 존재하고 해당 점에서 정의된 것에 의해 제공됩니다. 단일 실수 변수의 실수-값 함수(real-valued function)에 대해, 한 점에서 함수의 도함수는 일반적으로 해당 점에서 함수에 대한 최상의 선형 근사(linear approximation)를 결정합니다.

미분 미적분과 적분 미적분은 미적분의 기본 정리(fundamental theorem of calculus)에 의해 연결되며, 이것은 미분화는 적분화(integration)에 대한 역 과정임을 말합니다.

미분화는 거의 모든 양적 분야에 응용을 가집니다. 예를 들어, 물리학(physics)에서, 시간(time)에 관한 움직이는 물체의 변위(displacement)의 도함수는 물체의 속도(velocity)이고, 시간(time)에 관한 속도의 도함수는 가속도입니다. 물체의 운동량(momentum)의 도함수는 물체에 적용되는 힘과 같습니다; 이런 도함수 명제를 재정렬하면 운동의 뉴턴의 두 번째 법칙(Newton's second law of motion)과 결합된 유명한 F = ma 방정식으로 이어집니다. 화학 반응(chemical reaction)의 반응률(reaction rate)은 하나의 도함수입니다. 운용 연구(operations reaction)에서, 도함수는 자재 및 설계 공장을 운송하는 가장 효율적인 방법을 결정합니다.

도함수는 함수의 최대 및 최소(maxima and minima)를 찾는 것에 자주 사용됩니다. 도함수를 포함하는 방정식은 미분 방정식(differential equations)으로 불리고 자연 현상(natural phenomena)을 설명하는 것에 기본입니다. 도함수와 그의 일반화는 복소 해석학(complex analysis), 함수형 해석학(functional analysis), 미분 기하학(differential geometry), 측정 이론(measure theory), 및 추상 대수학(abstract algebra)과 같은, 수학의 많은 분야에 나타납니다.

The derivative

The tangent line at (x,f(x))

The derivative at different points of a differentiable function

Main article: Derivative

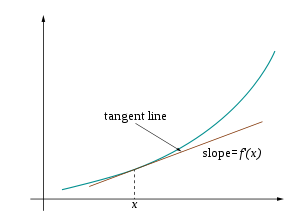
x와 y가 실수(real number)이고 y가 x의 함수(function); 즉, x의 모든 각 값에 대해, y의 대응하는 값이 있음을 가정합니다. 이 관계는 y = f(x)로 쓸 수 있습니다. 만약 f(x)가 (선형 방정식(linear equation)으로 불리는) 직선에 대한 방정식이면, y = mx + b를 만족하는 두 실수 m과 b가 있습니다. 이 "기울기-절편 형식"에서, 항 m은 기울기(slope)로 불리고 다음 공식으로부터 결정될 수 있습니다:

$m={\frac {{\text{change in }}y}{{\text{change in }}x}}={\frac {\Delta y}{\Delta x}},$

여기서 기호 Δ (그리스(Greek) 문자 델타(Delta)의 대문자 형태)는 "...에서 변화"에 대해 약어입니다. 그것은 Δy = m Δx임을 따릅니다.

일반적인 함수는 직선이 아니므로, 그것은 기울기를 가지지 않습니다. 기하학적으로, 점 x = a에서 f의 도함수(derivative of f at the point x = a)는 점 a에서 함수 f에 대한 접선(tangent line)의 기울기입니다 (그림을 참조하십시오). 이것은 종종 라그랑주의 표기법(Lagrange's notation)에서 f ′(a) 또는 라이프니츠의 표기법(Leibniz's notation)에서 dy/dx|_{x = a}로 표시됩니다. 도함수는 점 a에서 f에 대한 선형 근사의 기울기이므로, 도함수 (a에서 f의 값과 함께)는 점 a 근처에서 f의 최상의 선형 근사, 또는 선형화(linearization)를 결정합니다.

만약 f의 도메인에서 모든 각 점 a가 도함수를 가지면, 모든 점 a를 a에서 f의 도함수로 보내는 함수가 있습니다. 예를 들어, 만약 f(x) = x²이면, 도함수 함수 f ′(x) = dy/dx = 2x입니다.

밀접하게 관련된 개념은 함수의 미분(differential)입니다. x와 y가 실수 변수일 때, x에서 f의 도함수는 x에서 f의 그래프에 대한 접선의 기울기입니다. f의 소스와 타킷이 일-차원이기 때문에, f의 도함수는 실수입니다. 만약 x와 y가 벡터이면, f의 그래프에 대한 최상의 선형 근사는 f가 한 번에 여러 방향에서 어떻게 변화하는지에 달려 있습니다. 단일 방향에서 최상의 선형 근사를 취하는 것은 부분 도함수(partial derivative)를 결정하며, 이것은 보통 ∂y/∂x로 표시됩니다. 한 번에 모든 방향에서 f의 선형화는 전체 도함수(total derivative)로 불립니다.

History of differentiation

Main article: History of calculus

접선(tangent line)의 의미에서 도함수의 개념은, 유클리드(Euclid) (기원전 c. 300), 아르키메데스(Archimedes) (기원전 c. 287–212) 및 페르게의 아폴로니우스(Apollonius of Perga) (기원전 c. 262–190)와 같은 그리스(Greek) 기하학자들에게 친숙한, 매우 오래된 하나입니다. 아르키메데스(Archimedes)는, 비록 이들이 도함수와 접선보다는 넓이와 부피를 연구하기 위해 주로 사용되었을지라도, 무한소(infinitesimal)의 사용을 역시 도입했습니다; 무한소의 아르키메데스의 사용을 참조하십시오.

천문학자 및 수학자 아리아바타(Aryabhata) (476–550)가 달의 궤도(orbit of the Moon)를 연구하기 위해 무한소를 사용했을 때, 변화율을 연구하기 위해 무한소의 사용은, 아마도 서기 500년경, 인도 수학(Indian mathematics)에서 발견될 수 있습니다. 변화율을 계산하기 위해 무한소의 사용은 바스카라 II(Bhāskara II) (1114–1185)에 의해 현저하게 개발되었습니다; 실제로, 미적분학의 핵심 개념 중 다수가 "롤의 정리(Rolle's theorem)"와 같은 그의 연구에서 발견될 수 있다고 주장되어 왔습니다.

페르시아 수학자(Persian mathematician) 샤라프 알-딘 알-천(Sharaf al-Dīn al-Tūsī) (1135-1213)은, 그의 Treatise on Equations에서, 적절한 삼차 다항식의 최댓값을 찾는 것에 의한, 해를 가지기 위한 일부 삼차 방정식에 대해 조건을 세웠습니다. 그는, 예를 들어, 삼차 a x² — x³의 최댓값은 x = 2a/3일 때 발생함을 입증했고, 그것으로부터 방정식 a x² — x³ = c은 c = 4 a³/27일 때 정확히 하나의 양의 해를 가지고, 0 < c < 4 a³/27일 때마다 두 개의 양의 해를 가짐을 결론-내렸습니다. 과학의 역사가, 로쉬디 라시드(Roshdi Rashed)는 알-천이 이 결과를 얻기 위해 삼차의 도함수를 반드시 사용해 왔다고 주장해 왔습니다. 라시드의 결론은 다른 학자들에 의해 논쟁되어 왔으며, 어쨌든, 다른 학자들은 그가 알려진 함수의 도함수를 요구하지 않는 다른 방법에 의해 결과를 얻을 수 있다고 주장했습니다.

미적분학의 현대적 발전은 보통 아이작 뉴턴(Isaac Newton) (1643–1727) 및 고트프리트 라이프니츠(Gottfried Leibniz) (1646–1716)에게 공인되며, 그들은 미분화와 도함수에 대한 독립적이고 통일된 접근을 제공했습니다. 그들에게 이 신용을 받게 한, 어쨌든, 핵심 통찰력은 미분화와 적분화에 관련하는 미적분학의 기본 정리(fundamental theorem of calculus)였습니다; 이것은 넓이와 부피를 계산하는 것에 대해 쓸모없는 가장 이전의 방법을 세웠으며, 이븐 알-하이삼(Ibn al-Haytham) (Alhazen)의 시간 이후 현저하게 확장되어 오진 않았습니다. 도함수에 대한 그들의 아이디어에 대해, 뉴턴과 라이프니츠 둘 다는 피에르 드 페르마(Pierre de Fermat) (1607–1665), 아이작 배로(Isaac Barrow) (1630–1677), 르네 데카르트(René Descartes) (1596–1650), 크리스티안 하위헌스(Christiaan Huygens) (1629–1695), 블레즈 파스칼(Blaise Pascal) (1623–1662), 존 월리스(John Wallis) (1616–1703)와 같은 수학자들의 중요한 초기 작업을 바탕으로 세웠습니다. 페르마의 영향에 관련하여, 뉴턴은 "나는 접선을 그리는 페르마의 방법으로부터 [유율의] 이 방법의 힌트를 가졌고, 방정식을 추상하기 위해서, 직접 및 역으로, 그것을 적용하는 것에 의해, 나는 그것을 일반적으로 만들었습니다."라고 편지에 한번 썼습니다. 아이작 배로는 일반적으로 도함수의 초기 개발에 대해 명성을 얻었습니다. 그럼에도 불구하고, 뉴턴과 라이프니츠는 미분화의 역사에서 중요한 인물로 남아 있으며, 왜냐하면 뉴턴은 이론 물리학(theoretical physics)에 최초로 미분화를 적용했기 때문이며, 반면에 라이프니츠는 오늘날 여전히 사용되는 많은 표기법을 체계적으로 개발했습니다.

17세기 이후 많은 수학자들이 미분화의 이론에 대해 기여해 왔습니다. 19세기에서, 미적분학은 오귀스탱 루이 코시(Augustin Louis Cauchy) (1789–1857), 베른하르트 리만(Bernhard Riemann) (1826–1866), 및 카를 바이어슈트라스(Karl Weierstrass) (1815–1897)와 같은 수학자들에 의해 훨씬 더 엄격한 기준에 놓이게 되었습니다. 그것은 미분화가 유클리드 공간(Euclidean space)과 복소 평면(complex plane)으로 일반화된 것도 이 시기동안 이었습니다.

Applications of derivatives

Optimization

만약 f가 ℝ (또는 열린 구간(open interval)) 위에 미분-가능 함수(differentiable function)이고 x가 f의 지역적 최댓값(local maximum) 또는 지역적 최솟값(local minimum)이면, x에서 f의 도함수는 영입니다. f'(x) = 0인 점은 임계점(critical points) 또는 정류점(stationary point)으로 불립니다 (그리고 x에서 f의 값은 임계값(critical value)으로 불립니다.) 만약 f가 어디에서나 미분-가능이라는 가정을 하지 않으면, 그것이 미분-가능이 실패하는 점에서 역시 지명된 임계점입니다.

만약 f가 두 번 미분-가능이면, 역으로, f의 임계점 x는 x에서 f의 이차 도함수(second derivative)를 고려함으로써 해석될 수 있습니다:

• 만약 그것이 양수이면, x는 지역적 최솟값입니다;
• 만약 그것이 음수이면, x는 지역적 최댓값입니다;
• 만약 그것이 영이면, x는 지역적 최솟값, 지역적 최댓값, 또는 둘 다 아닐 수 있습니다.

(예를 들어, f(x) = x³는 x = 0에서 임계점을 가지지만, 그것은 그곳에서 최댓값 또는 최솟값을 가지므로, 반면에 f(x) = ± x⁴는 x = 0에서 임계점을 가지고, 그곳에서, 각각, 최솟값 및 최댓값을 가집니다.) 이것은 이차 도함수 테스트(second derivative test)로 불립니다. 일차 도함수 테스트(first derivative test)로 불리는, 대안적인 접근은 임계점의 각 변에서 f'의 부호를 고려하는 것을 포함합니다.

도함수를 취하고 임계점에 대해 푸는 것은 그러므로 직역적 최솟값 또는 최댓값을 찾기 위해 종종 간단한 방법이며, 이것은 최적화(optimization)에서 유용할 수 있습니다. 극단 값 정리(extreme value theorem)에 의해, 닫힌 구간(closed interval) 위의 연속 함수는 적어도 한 번 그의 최솟값과 최댓값을 도달해야 합니다. 만약 함수가 미분-가능이면, 최소 점과 최대 점은 오직 임계점 또는 끝점에서 발생할 수 있습니다.

이것은 그래프 스케치에서 응용을 역시 가집니다: 한번 미분-가능 함수의 지역적 최솟값과 최댓값은 찾아지면, 그래프의 개형은, 그것이 임계점 사이에서 증가 또는 감소할 수 있는 것이라는 관찰로부터 얻어질 수 있습니다.

고차원(higher dimension)에서, 스칼라-값(scalar value) 함수의 임계점은 그래디언트(gradient)가 영인 점입니다. 이차 도함수(second derivative) 테스트는 함수의 이차 부분 도함수의 헤세 행렬(Hessian matrix)의 고윳값(eigenvalue)을 고려함으로써 임계점을 해석하기 위해 여전히 사용될 수 있습니다. 만약 고윳값의 모두가 양수이면, 점은 지역적 최솟값입니다; 만약 모두가 음수이면, 그것은 지역적 최댓값입니다. 만약 일부 양 및 일부 음의 고윳값이 있으면, 임계점은 "안장점(saddle point)"으로 불리고, 만약 이들 경우의 어느 것도 유지되지 않으면 (즉, 고윳값의 일부가 영이면), 테스트는 결정적이지 않은 것으로 여겨집니다.

Calculus of variations

Main article: Calculus of variations

최적화 문제의 한 가지 예제는 다음입니다: 곡선이 곡면 위에 반드시 놓여 있어야 한다고 가정할 때, 곡면 위의 두 점 사이에서 가장 짧은 곡선을 찾는 것입니다. 만약 곡면이 평면이면, 가장 짧은 곡선은 직선입니다. 그러나 만약 곡면이, 예를 들어, 계란-모양이면, 최단 경로(shortest path)가 바로 명확하지 않습니다. 이들 경로는 지오데식(geodesic)으로 불리고, 변형의 미적분학에서 가장 기본적인 문제 중 하나는 지오데식을 찾는 것입니다. 또 다른 예제는 다음입니다: 공간에서 닫힌 곡선으로 채우는 가장-작은 넓이 곡면을 찾는 것입니다. 이 곡면은 최소 곡면(minimal surface)으로 불리고, 그것은, 역시, 변형의 미적분학을 사용하여 구할 수 있습니다.

Physics

미적분학은 물리학에서 치명적으로 중요합니다: 많은 물리적 프로세서가, 미분 방정식(differential equation)으로 불리는, 도함수를 포함하는 방정식에 의해 묘사됩니다. 물리학은 특히 시간이 지남에 따라 양이 변화하고 발전하는 방법에 관심이 있으며, "시간 도함수(time derivative)"— 시간에 걸쳐 변화율 —의 개념은 여러 중요한 개념의 정확한 정의에 대해 필수적입니다. 특히, 물체의 위치의 시간 도함수는 뉴턴 물리학(Newtonian physics)에서 중요합니다:

• 속도(velocity)는 물체의 변위 (원래 위치로부터의 거리)의 (시간에 관한) 도함수입니다.
• 가속도(acceleration)는 물체의 속도의 (시간에 관한) 도함수입니다, 즉, 물체의 위치의 (시간에 관한) 이차 도함수입니다.

예를 들어, 만약 직선 위의 물체의 위치는 다음에 의해 제공됩니다:

$x(t)=-16t^{2}+16t+32,\,\!$

물체의 속도는 다음입니다:

${\dot {x}}(t)=x'(t)=-32t+16,\,\!$

및 물체의 가속도는 다음입니다:

${\ddot {x}}(t)=x''(t)=-32,\,\!$

이것은 상수입니다.

Differential equations

Main article: Differential equation

미분 방정식은 함수 모음과 그들의 도함수 사이의 관계입니다. 보통의 미분 방정식(ordinary differential equation)은 하나의 변수의 함수를 해당 변수와 관한 그들의 도함수와 관련시키는 미분 방정식입니다. 부분 미분 방정식(partial differential equation)은 둘 이상의 변수의 함수를 그들의 부분 도함수(partial derivative)와 관련시키는 미분 방정식입니다. 미분 방정식은 물리적 과학, 수학적 모델링, 및 수학 자체에서 자연스럽게 발생합니다. 예를 들어, 뉴턴의 두 번째 법칙(Newton's second law)은 가속도와 힘 사이의 관계를 기술하며, 다음 보통의 미분 방정식으로 말할 수 있습니다:

$F(t)=m{\frac {d^{2}x}{dt^{2}}}.$

직선 막대를 통해 열이 어떻게 확산되는지를 설명하는, 하나의 공간 변수에서 열 방정식(heat equation)은 다음 부분 미분 방정식입니다:

${\frac {\partial u}{\partial t}}=\alpha {\frac {\partial ^{2}u}{\partial x^{2}}}.$

여기서 u(x,t)는 위치 x와 시간 t에서 막대의 온도이고 α는 막대를 통해 얼마나 빠르게 열이 확산되는지에 의존하는 상수입니다.

Mean value theorem

Main article: Mean value theorem

The mean value theorem: For each differentiable function $f:[a,b]\to \mathbb {R}$ with $a<b$ there is a $c\in (a,b)$ with $f'(c)={\tfrac {f(b)-f(a)}{b-a}}$.

평균값 정리는 도함수의 값과 원래 함수 값 사이의 관계를 제공합니다. 만약 f(x)가 실수-값 함수이고 a와 b가 a < b을 갖는 숫자이면, 평균값 정리는 가벼운 가설 아래에서, 두 점 (a, f(a))와 (b, f(b)) 사이의 기울기는 a와 b 사이의 어떤 점 c에서 f에 대한 접선의 기울기와 같음을 말합니다. 다른 말로,

$f'(c)={\frac {f(b)-f(a)}{b-a}}.$

연습에서, 평균값 정리가 하는 것은 그의 도함수의 관점에서 함수를 제어하는 것입니다. 예를 들어, f가 각 점에서 영과 같은 도함수를 갖는다고 가정합니다. 이것은 그의 접선이 모든 각 점에서 수평이므로, 함수가 역시 반드시 수평이어야 함을 의미합니다. 평균값 정리는 이것이 반드시 참임을 입증합니다: f의 그래프 위에 임의의 두 점 사이의 기울기는 f의 접선 중 하나의 기울기와 반드시 같습니다. 그들 기울기의 모두는 영이므로, 그래프 위의 한 점에서 다른 점까지의 임의의 직선은 역시 기울기가 영일 것입니다. 그러나 함수가 위 또는 아래로 움직이지 않는다는 것을 의미하므로, 반드시 수평 직선이 되어야 함을 말합니다. 도함수에 대한 보다 복잡한 조건은 원래 함수에 대한 덜 정확하지만 여전히 매우 유용한 정보로 이어집니다.

Taylor polynomials and Taylor series

Main articles: Taylor polynomial and Taylor series

도함수는 주어진 점에서 함수의 최상의 가능한 선형 근사를 제공하지만, 이것은 원래 함수로부터 매우 다를 수 있습니다. 근사를 개선하는 한 가지 방법은 이차 근사를 취하는 것입니다. 즉 다시 말해서, 점 x₀에서 실수-값 함수 f(x)의 선형화는 선형 다항식 a + b(x − x₀)이고, 이차 다항식 a + b(x − x₀) + c(x − x₀)²을 고려함으로써 더 좋은 근사를 얻는 것이 가능할 것입니다. 여전히 더 나은 것은 삼차 다항식 a + b(x − x₀) + c(x − x₀)² + d(x − x₀)³일 수 있고, 이 아이디어는 임의로 고차 다항식으로 확장될 수 있습니다. 이들 다항식 각각에 대해, 근사를 가능한 한 좋게 만드는 계수 a, b, c, 및 d의 최상의 가능한 선택이 반드시 있어야 합니다.

x₀의 이웃(neighbourhood)에서, a에 대해 최선의 가능한 선택은 항상 f(x₀)이고, b에 대해 최선의 가능한 선택은 항상 f'(x₀)입니다. c, d, 및 상위-차수 계수에 대해, 이들 계수는 f의 더 높은 도함수에 의해 결정됩니다. c는 항상 f''(x₀)/2이어야 하고, d는 항상 f'''(x₀)/3!이어야 합니다. 이들 계수를 사용하면 f의 테일러 다항식(Taylor polynomial)을 제공합니다. 차수 d의 테일러 다항식은 f를 최상으로 근사하는 차수 d의 다항식이고, 그의 계수는 위의 공식의 일반화에 의해 구할 수 있습니다. 테일러 정리(Taylor's theorem)는 근사가 얼마나 좋은지에 대한 정확한 경계를 제공합니다. 만약 f가 차수 d보다 작거나 같은 다항식이면, 차수 d의 테일러 다항식은 f와 같습니다.

테일러 다항식의 극한은 테일러 급수(Taylor series)로 불리는 무한 급수입니다. 테일러 급수는 원래 함수에 대한 자주 매우 좋은 근사입니다. 그들 테일러 급수와 같은 함수는 해석적 함수(analytic function)로 불립니다. 불연속성 또는 예리한 구석이 있는 함수는 해석적일 수는 없지만, 해석적이지 않은 매끄러운 함수(smooth function)가 있습니다.

Implicit function theorem

Main article: Implicit function theorem

원(circle)과 같은, 일부 자연적인 기하학 모양은 함수의 그래프(graph of a function)로 그려질 수 않습니다. 예를 들어, 만약 f(x, y) = x² + y² − 1이면, 원은 f(x, y) = 0를 만족하는 모든 쌍 (x, y)의 집합입니다. 이 집합은 f의 영 집합이라고 불리고, f의 그래프와 같지 않고, 이것은 포물면체(paraboloid)입니다. 암시적 함수 정리는 f(x, y) = 0와 같은 관계를 함수로 변환합니다. 그것은, 만약 f가 연속적으로 미분-가능(continuously differentiable)이면, 대부분의 점 주변으로, f의 영 집합은 함께 붙여진 함수의 그래프처럼 보입니다. 이것이 사실이 아닌 점은 f의 도함수에 대한 조건에 의해 결정됩니다. 원은, 예를 들어, 두 함수 ± √1 - x²의 그래프에서 함께 붙여넣을 수 있습니다. (−1, 0)와 (1, 0)을 제외한 원 위의 모든 각 점 이웃에서, 이들 두 함수 중 하나는 원과 비슷한 그래프를 가집니다. (이들 두 함수는 (−1, 0)와 (1, 0)에서 역시 만나기도 하지만, 이것은 암시적 함수 정리에 의해 보장되지는 않습니다.)

암시적 함수 정리는 역함수 정리(inverse function theorem)와 밀접하게 관련되어 있으며, 이것은 함수가 함께 붙여진 역-가능 함수(invertible function)의 그래프처럼 보일 때를 말합니다.

See also

• Differential (calculus)
• Differential geometry
• Numerical differentiation
• Techniques for differentiation
• List of calculus topics

References

• J. Edwards (1892). Differential Calculus. London: MacMillan and Co. p. 1.