Integral

수학(mathematics)에서, 적분(integral)은 무한소(infinitesimal) 데이터를 연결함으로써 발생하는 변위, 넓이, 부피, 및 다른 개념을 설명할 수 있는 방법으로 숫자를 함수에 할당합니다. 적분은 미적분학(calculus)의 두 주요 연산 중 하나이며, 나머지 하나는, 그의 역, 미분화(differentiation)입니다. 실수(real) 변수(variable) $x$ 의 함수(function) $f$ 및 실수 직선(real line)의 구간(interval) $[a, b]$ 가 주어지면, 한정 적분(definite integral)

\int _{a}^{b}f(x)\,dx

는 $f$ 의 그래프(graph), $x$ -축 및 수직 직선 $x = a$ 와 $x = b$ 로 경계짓는 $xy$ -평면에서 영역의 부호화된 넓이(area)로 비공식적으로 이해될 수 있습니다. $x$ -축 위의 넓이는 총량에 더해지고 $x$ -축 아래의 것은 총량에서 뺍니다.

적분화의 연산은, 더해지는 상수까지(up to), 미분화의 연산의 역입니다. 이런 이유로, 용어 적분(integral)은 역도함수(antiderivative)의 관련 개념, 즉 그의 도함수(derivative)가 주어진 함수 $f$ 인 함수 $F$ 를 역시 참조할 수 있습니다. 이 경우에서, 그것은 부정 적분(indefinite integral)으로 불리고 다음으로 쓰입니다:

F(x)=\int f(x)\,dx.

이 기사에서 논의되는 적분은 한정 적분(definite integrals)으로 이름 짓는 것입니다. 그것은 미분화와 한정 적분을 연결시키는 미적분의 기본 정리(fundamental theorem of calculus)입니다: 만약 $f$ 가 닫힌 구간(closed interval) $[a, b]$ 에서 정의된 연속적인 실수-값 함수이면, 일단 $f$ 의 역도함수 $F$ 가 알려지고, 해당 구간에 걸친 $f$ 의 한정 적분은 다음으로 제공됩니다:

\int _{a}^{b}\,f(x)dx=\left[F(x)\right]_{a}^{b}=F(b)-F(a)\,.

적분화의 원리는 17세기 후반에 아이작 뉴턴(Isaac Newton) 및 고트프리트 라이프니츠(Gottfried Leibniz)에 의해 독립적으로 공식화되었으며, 그들은 적분을 무한소(infinitesimal) 너비의 직사각형의 무한 합으로 생각했습니다. 베른하르트 리만(Bernhard Riemann)은 적분의 엄격한 수학적 정의를 제공했습니다. 그것은 영역을 얇은 수직 슬랩으로 나누어서 곡선(curvilinear) 영역의 넓이를 근사화하는 극한하는 절차를 기반으로 합니다. 19세기에 들어서면서, 적분의 보다 정교한 개념이 나타나기 시작했으며, 여기서 함수의 유형과 마찬가지로 적분이 수행되는 도메인(domain)이 일반화되어 왔습니다. 곡선 적분(line integral)은 둘 이상의 변수의 함수에 대해 정의되고, 적분화의 구간 $[a, b]$ 는 두 점을 연결하는 곡선(curve)으로 대체됩니다. 표면 적분(surface integral)에서, 곡선은 삼-차원 공간(three-dimensional space)에서 표면(surface)의 조각으로 대체됩니다.

History

Pre-calculus integration

적분을 결정할 수 있는 첫 번째 문서화된 체계적인 기법은 고대 그리스 천문학자 에우독소스(Eudoxus) (기원전 ca. 370)의 소진의 방법(method of exhaustion)이며, 이것은 그들을 무한 숫자의 넓이 또는 부피가 알려진 부분으로 나눔으로써 넓이 및 부피를 구하려고 생각했습니다. 이 방법은 기원전 3세기에 아르키메데스(Archimedes)에 의해 더욱이 개발되고 적용되었고 포물선(parabola)에 대한 넓이 및 원의 넓이(area of a circle)에 대한 근사를 계산하기 위해 사용되었습니다.

비슷한 방법은 유 휘(Liu Hui)에 의해 기원후 3세기 경에 중국에서 독립적으로 개발되었으며, 그는 그것을 원의 넓이를 구하기 위해서 사용했습니다. 이 방법은 나중에 구의 부피를 찾기 위해 중국의 아버지-와-아들 수학자 조충지(Zu Chongzhi)와 조긍지(Zu Geng)에 의해 5세기에 사용되었습니다 (Shea 2007; Katz 2004, pp. 125–126).

중동에서, 알하젠(Alhazen) (c. 965 – c. 1040 CE)으로 라틴어화된, 하산 이븐 알-하이삼(Hasan Ibn al-Haytham)은 네 번째 거듭제곱(fourth power)의 합에 대해 공식을 도출했습니다. 그는 지금 이 함수의 적분(integration)으로 불리는 것을 수행하기 위해 결과를 사용했으며, 여기서 적분 제곱과 네 번째 거듭제곱의 합에 대한 공식은 그에게 포물면체(paraboloid)의 부피를 계산하는 것을 허용했습니다.^[1]

적분 미적분학에서 다음 중요한 진보는 17세기까지 나타나지 않았습니다. 이 시점에서, 그의 비-분할의 방법(method of Indivisibles)과 함께 카발리에리(Cavalieri)의 연구 및 페르마(Fermat)에 의한 연구는 카발리에리가 카바리에리의 구적법 공식(Cavalieri's quadrature formula)에서 차수 $n = 9$ 까지 $x n$ 의 적분을 계산하는 것과 함께, 현대 미적분학의 기초를 세우기 시작했습니다. 뒤따른 단계는 17세기 초에 배로(Barrow) 및 토리첼리(Torricelli)에 의해 만들어 졌으며, 그는 적분화와 미분화(differentiation) 사이의 연결의 첫 번째 힌트를 제공했습니다. 배로는 미적분학의 기본 정리(fundamental theorem of calculus)의 첫 번째 증명을 제공했습니다. 월리스(Wallis)는 카발리에리의 방법을 일반화했으며, $x$ 의 적분을, 음의 거듭제곱과 분수 거듭제곱을 포함하는, 일반적인 거듭제곱으로 계산합니다.

Newton and Leibniz

적분화에서 주요 발전은 라이프니츠(Leibniz)와 뉴턴(Newton)에 의해 미적분학의 기본 정리(fundamental theorem of calculus)의 독립적인 발견과 함께 17세기에 시작되었습니다. 정리는 적분화와 미분화 사이의 연결을 증명했습니다. 비교가 쉬운 미분화와 결합된, 이 연결은 적분을 계산하기 위해 개발될 수 있습니다. 특히, 미적분학의 기본 정리는 우리에게 문제의 보다 광범위한 클래스를 해결하는 것을 허용합니다. 중요성에서 대등한 것은 뉴턴과 라이프니츠 둘 다가 개발한 포괄적인 수학 프레임워크입니다. 이름 무한소 미적분학이 주어지면, 그것은 연속 도메인 이내의 함수의 정밀한 분석에 대해 허용합니다. 이 프레임워크는 결국 현대 미적분학(calculus)이 되었고, 적분에 대한 그의 표기법은 라이프니츠의 연구로부터 직접 추출되었습니다.

Formalization

뉴턴과 라이프니츠는 적분화에 대해 체계적인 접근을 제공했지만, 그들의 업적은 엄격함(rigour)의 정도에서 부족했습니다. 버클리 주교(Bishop Berkeley)는 뉴턴에 의해 사용된 사라지는 증분을 잊지-않고 공격하여, 그들을 "떠난 양의 유령(ghosts of departed quantities)"으로 불렀습니다. 미적분학은 극한(limits)의 개발과 함께 확고한 발판을 얻었습니다. 적분화는, 리만(Riemann)에 의해, 극한을 사용하여, 처음으로 엄격하게 공식화되었습니다. 비록 모든 경계진 조각별 연속 함수는 경계화된 구간에서 리만-적분가능이지만, 이후 보다 일반적인 함수는 리만(Riemann)의 정의가 적용되지 않는 것—특별히 푸리에 해석학(Fourier analysis)의 문맥에서—에 대해 고려되었으며, 르베그(Lebesgue)는 (실수 해석학(real analysis)의 부분-필드) 측정 이론(measure theory)에 기초를 둔, 적분의 다른 정의를 공식화했습니다. 리만과 르베그의 접근을 확장하는, 적분의 다른 정의가 제안되었습니다. 실수 시스템을 기반으로 한 이들 접근은 오늘날 가장 공통적인 하나이지만, 초실수(hyperreal number) 시스템을 기반으로 한, 무한 리만 합의 표준 부분(standard part)으로 적분의 정의와 같은, 대안적인 접근이 존재합니다.

Historical notation

부정 적분에 대해 표기법은 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz)에 의해 1675년에 도입되었습니다 (Burton 1988, p. 359; Leibniz 1899, p. 154). 그는, summa (ſumma로 쓰이는; "sum" 또는 "total"에 대한 라틴어)를 나타내는, 문자 ſ (긴 s)로부터, 적분 기호(integral symbol), ∫를 개조했습니다. 적분 기호의 위와 아래의 극한과 함께, 한정 적분에 대해 현대 표기법은 1819–20년경 프랑스 학술원의 Mémoires에서 조제프 푸리에(Joseph Fourier)에 의해 처음으로 사용되었고, 1822년 그의 저서에 재판되었습니다 (Cajori 1929, pp. 249–250; Fourier 1822, §231).

아이작 뉴턴(Isaac Newton)은 적분화를 나타내기 위해 변수 위에 작은 수직 막대를 사용하는 것, 또는 변수를 상자 안에 배치했습니다. 수직 막대는 $. x$ 또는 $x'$ 와 쉽게 혼동되었으며, 이것은 미분화를 나타내기 위해 사용되었고, 상자 표기법은 재생산하기 위해 프린터에 대해 어려웠으므로, 이들 표기법은 널리 채택되지 않았습니다.

Applications

적분은 수학 분야의 많은 분야 뿐만 아니라 수학에 의존하는 많은 다른 분야에서 광범위하게 사용됩니다.

예를 들어, 확률 이론(probability theory)에서, 적분은 특정 범위 이내에 떨어지는 어떤 확률 변수(random variable)의 확률을 결정하기 위해 사용됩니다. 게다가, 전체 확률 밀도 함수(probability density function) 아래에 적분은 반드시 1과 같아야 하며, 이것은 음수 값을 갖지 않는 함수(function)가 밀도 함수가 될 수 있는지 여부의 테스트를 제공합니다.

적분은 곡선 경계를 갖는 이-차원 영역의 넓이(area)를 계산하는 것, 마찬가지로 곡선 경계를 갖는 삼-차원 대상의 부피를 계산하는 것(Volume integral)에 대해 사용될 수 있습니다. 이차원 영역의 넓이는 앞에-언급된 한정 적분을 사용하여 계산될 수 있습니다.

디스크 또는 세탁기와 같은 삼-차원 대상의 부피는, 디스크 적분화(Disc integration)에서 요약된 것처럼, 원기둥의 부피에 대한 방정식, $\pi r^{2}h$ 을 사용하여 계산될 수 있으며, 여기서 $r$ 은 반지름이며, 그것은 이 경우에서 함수의 곡선에서 그것이 회전하는 직선까지의 거리일 것입니다. 간단한 디스크에 대해, 반지름은 함수에서 직선의 주어진 $x$ -값 또는 $y$ -값을 뺀 방정식일 것입니다. 예를 들어, 직선 $y=-1$ 을 중심으로 이차 $y=-x^{2}+4$ 를 회전시켜 만든 디스크의 반지름은 표현 $-x^{2}+4-(-1)$ 또는 $-x^{2}+5$ 에 의해 제공될 것입니다. 이 같은 모양에 대해 부피를 찾기 위해서, $a$ 와 $b$ 가 이차 $y=-x^{2}+4$ 및 직선 $y=-1$ 의 교차점을 만족하는 경계 $a$ 와 $b$ 를 가진 적분은 다음으로 사용될 것입니다: $\pi \int _{a}^{b}(-x^{2}+5)^{2}\,dx$ 위의 적분의 성분은 원기둥의 부피에 대해 방정식, $\pi r^{2}h$ 에서 변수를 나타냅니다. 상수 π는 인수로 묶어내지만, 반지름, $-x^{2}+5$ 은 적분 속에서 제곱됩니다. $h$ 에 의해 부피 공식에서 나타내는, 높이는 (가장-큰 가능한 정확도와 함께 부피를 근사하기 위해) 무한소적으로 작은 항 $dx$ 에 의해 이 적분에서 제공됩니다.

적분은, 변위(displacement), 시간(time) 및 속도(velocity)와 같은 양을 찾기 위해 운동학(kinematics)과 같은 분야에서, 물리학에서 역시 사용됩니다. 예를 들어, 직선 운동에서, 시간 구간 $[a,b]$ 에 걸쳐 대상의 변위는 다음으로 제공됩니다:

x(b)-x(a)=\int _{a}^{b}v(t)\,dt,

여기서 $v(t)$ 는 시간의 함수로 표현된 속도입니다. 초기 위치 $A$ 에서 최종 위치 $B$ 까지 (위치의 함수로 주어진) 힘 $F(x)$ 에 의해 행해진 일은 다음입니다:

W_{A\rightarrow B}=\int _{A}^{B}F(x)\,dx.

적분은 열역학(thermodynamics)에서 역시 사용되며, 여기서 열역학적 적분(thermodynamic integration)은 두 주어진 상태 사이의 자유 에너지에서 차이를 계산하기 위해 사용됩니다.

Terminology and notation

Standard

구간 $[a, b]$ 위에 실수 변수 $x$ 의 실수-값 함수(real-valued function) $f$ 의 $x$ 에 관한 적분은 다음으로 쓰입니다:

\int _{a}^{b}f(x)\,dx.

적분 기호 $\int$ 는 적분화를 나타냅니다. 변수 $x$ 의 미분(differential)으로 불리는, 기호 $dx$ 는 적분화의 변수가 $x$ 임을 나타냅니다. 적분되어질 함수 $f (x)$ 는 피적분(integrand)으로 불립니다. 기호 $dx$ 는 (보이는 것처럼) 간격에 의해 피적분으로부터 분리됩니다. 함수는, 만약 그의 도메인에 걸친 함수의 적분이 유한하면, 적분-가능이라고 말합니다. 점 $a$ 와 $b$ 는 적분의 극한이라고 불립니다. 극한이 명시된 적분은 한정 적분으로 불립니다. 적분은 구간 $[a, b]$ 에 관한 것이라고 말합니다.

만약 적분이 유한 값 a에서 위쪽 극한 무한대로 가면, 적분은, b가 무한대로 갈 때, a에서 값 b로의 적분의 극한을 표현합니다. 만약 적분의 값이 유한 값에 점점 더 가까워지면, 적분은 해당 값으로 수렴(converge)한다고 말합니다. 만약 아니면, 적분은 발산한다고 말합니다.

다음처럼, 극한이 생략되었을 때,

\int f(x)\,dx,

적분은 부정 적분으로 불리며, 이것은 그의 도함수가 피적분인 함수 (역도함수(antiderivative))의 클래스를 나타냅니다. 미적분학의 기본 정리(fundamental theorem of calculus)는 한정 적분의 평가를 부정 적분에 관련시킵니다. 때때로, 적분화의 극한은, 같은 극한이 특정 문맥에서 반복적으로 발생할 때, 한정 적분에 대해 생략됩니다. 보통, 저자는 관련 텍스트의 시작 부분에서 이 관례를 명확하게 할 것입니다.

비경계진 도메인 위에서 및/또는 다 차원에서 적분화를 포괄하는 적분에 대한 표기법의 여러 확장이 있습니다 (이 기사 뒷 부분을 참조하십시오).

Meaning of the symbol dx

역사적으로, 기호 dx는 무한 의미에서 합해지고 피적분에 의해 곱해지게 되는 독립 변수(independent variable) x의 무한소적으로 "작은 조각"을 나타내기 위해서 취해졌습니다. 이 개념은 여전히 휴리스틱적으로 유용하지만, 나중에 수학자들의 실수 시스템의 관점으로부터 무시할 수 없는 무한소 양으로 생각되어 왔습니다.^[2] 미적분학 도입에서, 표현 dx는 그러므로 독립적인 의미로 지정되지 않습니다; 대신에, 그것은 적분화에 대해 기호의 부분으로 보이고 적분되려는 표현의 오른쪽에 그의 구분 기호로 사용됩니다.

보다 정교한 문맥에서, dx는 그 자체로 중요성을 가질 수 있으며, 그것의 의미는 논의하려는 수학의 특정 분야에 따라 다릅니다. 이들 방법 중 하나에서 사용될 때, 원래의 라이프니츠 표기법은 적분의 원래의 정의의 일반화에 적용하기 위해 공동-선택됩니다. dx의 일부 공통적인 해석은 다음을 포함합니다: (일반적으로 dα(x)로 표시되는) 리만–시틸티어스 적분화(Riemann–Stieltjes integral)에서 적분기 함수, (일반적으로 dμ로 표시되는) 르베그 이론에서 측정(measure), 또는 (일반적으로 $dx^{i_{1}}\wedge \cdots \wedge dx^{i_{k}}$ 로 표시되는) 외부 미적분학에서 미분 형식(differential form). 마지막 경우에서, 심지어 문자 d는 독립적인 의미를 가집니다 — 미분 형식의 외부 도함수(exterior derivative) 연산자입니다.

반대로, 고급 설정에서, 그것은 오직 간단한 리만 적분이 사용되었을 때, 또는 적분의 정확한 유형이 중요하지 않을 때, dx를 생략하는 것이 드문 것은 아닙니다. 예를 들어, 우리는, 리만 적분과 그것으로부터 모든 일반화에 의해 공유되는 속성, 적분의 선형성을 표현하기 위해 ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ 를 쓸 수 있을 것입니다.

Variants

현대 아랍어 수학 표기법(modern Arabic mathematical notation)에서, 비쳐진 적분 기호 는 기호 $\int$ 대신에 사용되는데, 왜냐하면 아랍어 스크립트와 수학 표현은 오른쪽에서 왼쪽으로 가기 때문입니다.^[3] 특히 유럽에 출신의 일부 저자는 적분화의 변수를 나타내기 위해 직립 "d" (즉, $dx$ 대신에 $d x$ )를 사용하는데, 왜냐하면 정확히 말하자면, "d"는 변수가 아니기 때문입니다. 역시, 기호 $dx$ 는, 예를 들어 다음에서 처럼, $f (x)$ 다음에 항상 위치되지는 않습니다:

\int \limits _{0}^{1}{\frac {3\ dx}{x^{2}+1}}\quad

또는

\quad \int _{0}^{1}dx\int _{0}^{1}dy\ e^{-(x^{2}+y^{2})}

.

첫 번째 표현에서, 미분은 무한소 "곱셉의" 인수, 표현 3/(x²+1)에 "곱해질" 때 공식적으로 "교환 속성"을 따르는 것으로 취급됩니다. 두 번째 표현에서, 미분이 먼저 보이는 것은, 물리학자에게 특별히 인기 있는 업무, 그것에 관해 적분되려는 변수를 강조하고 명확하게 합니다.

Interpretations of the integral

적분은 많은 실제 상황에서 나타납니다. 만약 수영장이 평평한 바닥을 갖는 직사각형이면, 그의 길이, 너비 및 깊이로부터 우리는 그것이 (그것을 채우기 위한) 포함하는 물의 부피, (그것을 덮기 위한) 그의 표면의 넓이, 및 (그것을 밧줄을 묶기 위한) 그의 가장자리의 길이를 쉽게 결정할 수 있습니다. 그러나 만약 그것이 둥근 바닥을 가진 계란형이면, 이들 양의 모두는 적분을 요구합니다. 실제적인 근사가 그러한 자명한 예제에 대해 충분할 수 있을 것이지만, (임의의 분야의) 정밀 공학(precision engineering)은 이들 원소에 대해 정확하고 엄격한 값을 요구합니다.

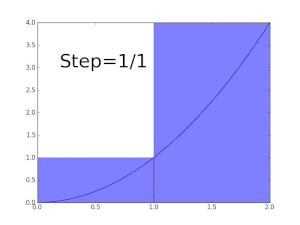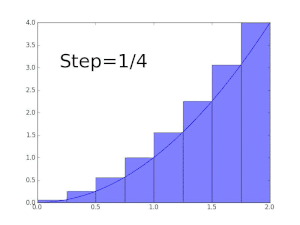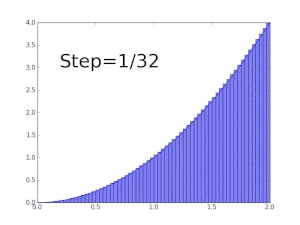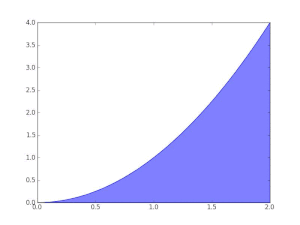
시작하기 위해, $f (x) = \sqrt x$ 를 갖는 $x = 0$ 와 $x = 1$ 사이의 곡선 $y = f (x)$ 를 생각해 보십시오 (그림을 참조하십시오). 우리는 다음을 물어봅니다:

구간 0에서 1 사이에서, 함수

f

아래의 넓이는 무엇입니까?

그리고 이것 (아직 알려지지 않은) 넓이를 $f$ 의 (정)적분으로 부릅니다. 이 적분에 대한 표기법은 다음일 것입니다:

\int _{0}^{1}{\sqrt {x}}\ dx.

첫 번째 근사처럼, 변 $x = 0$ 에서 $x = 1$ 및 $y = f (0) = 0$ 및 $y = f (1) = 1$ 에 의해 주어지는 단위 사각형을 보십시오. 그의 넓이는 정확히 1입니다. 실제로, 적분의 참값은 반드시 1보다 약간 작아야 합니다. 근사 직사각형의 너비를 줄이고 직사각형 숫자를 늘리는 것은 더 나은 결과를 제공합니다; 그래서 근사 점 0, 1/5, 2/5, 및 계속해서 1까지를 사용하여, 다섯 단계에서 구간에 줄을 긋습니다. 각 곡선 조각의 오른쪽 끝 높이를 사용하여 각 단계에 대해 상자를 맞추고, 따라서 $\sqrt 1/5$ , $\sqrt 2/5$ , 및 계속해서 $\sqrt 1 = 1$ 까지입니다. 이들 직사각형의 넓이를 합하는 것은, 우리는 추구하는 적분에 대해 더 나은 근사를 얻습니다. 즉

\textstyle {\sqrt {\frac {1}{5}}}\left({\frac {1}{5}}-0\right)+{\sqrt {\frac {2}{5}}}\left({\frac {2}{5}}-{\frac {1}{5}}\right)+\cdots +{\sqrt {\frac {5}{5}}}\left({\frac {5}{5}}-{\frac {4}{5}}\right)\approx 0.7497.

우리는 두 후속 근사 점의 차이와 곱해지는, $f$ 의 유한하게 많은 함수 값의 합을 취하는 것입니다. 우리는 근사가 너무 크다는 것을 쉽게 알 수 있습니다. 더 많은 단계를 사용하면 더 가까운 근사를 제공하지만, 항상 너무 높아질 수 있고 결코 정확하게 될 수 없을 것입니다. 대안적으로, 각 조각의 왼쪽 끝 높이를 갖는 조각에 의해 이들 부분-구간을 대체하면, 우리는 너무 낮은 근사를 얻게될 것입니다: 예를 들어, 열두 개의 그런 부분-구간과 함께 우리는 0.6203의 넓이에 대한 근사 값을 얻을 것입니다.

핵심 아이디어는 그들 각각의 함수 값에 의해 곱해진 근사 점의 유한하게 많은 차이를 더하는 것에서 무한하게 많은 미세한, 또는 무한소(infinitesimal) 단계를 사용하는 것으로의 전환입니다. 이 전환이 위의 예제에서 완료될 때, 그것은 지정된 경계 이내에 곡선 아래 넓이가 2/3이라는 것이 밝혀집니다.

표기법

\int f(x)\ dx

은 적분을 함수 값, $f (x)$ 에, $dx$ 로 표시되는, 소위 미분이라는, 무한소 단계 너비를 곱한, 가늘고 긴 $s$ 로 표시되는, 가중된 합으로 이해합니다.

역사적으로, 무한소를 엄격하게 해석하기 위한 초기 노력의 실패 후에, 리만은, $dx$ 는 차이 (즉, 구간 폭)의 극한으로 암시하게 되도록, 가중된 합의 극한(limit)으로 적분을 공식적으로 정의했었습니다. 구간과 연속성에 대한 리만의 의존의 결점은 더 새로운 정의에 동기를 부여했으며, 특히 르베그 적분(Lebesgue integral), 이것은 훨씬 더 유연한 방법으로 "측정"의 아이디어를 확장하는 능력에 기초됩니다. 따라서 표기법

\int _{A}f(x)\ d\mu

은, 함수 값은 각 값에 할당되는 가중을 측정하는 $μ$ 와 함께 분할된 것에서, 가중화된 합을 참조합니다. 여기서 $A$ 는 적분화의 영역을 나타냅니다.

Darboux sums

Darboux upper sums of the function

y = x 2

Darboux lower sums of the function

y = x 2

Formal definitions

Integral example with irregular partitions (largest marked in red)

Riemann sums converging

적분을 공식적으로 정의하는 여러 가지 방법이 있지만, 그들 모두가 동등하지는 않습니다. 차이는 대부분 다른 정의 아래에서 적분될 수 없을 수 있는 의견을 달리하는 특별한 경우를 다루기 위한 것이지만, 때때로 교육학상의 이유로 역시 존재합니다. 적분의 가장 공통적으로 사용되는 정의는 리만 적분과 르베그 적분입니다.

Riemann integral

리만 적분은 구간의 태그화 분할에 관한 함수의 리만 합(Riemann sum)의 관점에서 정의됩니다.^[4] $[a, b]$ 를 실수 직선의 닫힌 구간(closed interval)으로 놓습니다; 그런-다음 $[a, b]$ 의 태그화 분할은 다음 유한 수열입니다:

a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!

구간 $[a, b]$ 를 $i$ 에 의해 인덱스된 $n$ 부분-구간 $[x i -1, x i]$ 으로 이 분할, 이것의 각각은 두드러진 점 $t i \in [x i -1, x i]$ 을 갖는 "태그화"입니다. 그러한 태그화 분할에 관한 함수 $f$ 의 리만 합은 다음으로 정의됩니다:

\sum _{i=1}^{n}f(t_{i})\,\Delta _{i};

따라서 합의 각 항은 주어진 부분-구간의 두드러진 점에서 함수 값과 같은 높이를 갖는, 및 부분-구간 폭과 같은 폭을 갖는 직사각형의 넓이입니다. $Δ i = x i - x i -1$ 를 부분-구간 $i$ 의 너비로 놓습니다; 그러한 태그화 분할의 그물(mesh)은 분할에 의해 형성된 가장 큰 부분-구간의 너비, $max i =1... n Δ i$ 입니다. 구간 $[a, b]$ 에 걸친 함수 $f$ 의 리만 적분은, 만약 다음이면, $S$ 와 같습니다:

모든

ε > 0

에 대해,

δ

보다 작은 그물을 갖는 임의의 태그화 분할

[a, b]

에 대해, 우리는 다음을 가지는 것을 만족하는

δ > 0

가 존재합니다:

\left|S-\sum _{i=1}^{n}f(t_{i})\,\Delta _{i}\right|<\varepsilon .

선택된 태그가 각 구간의 최댓값 (각각 최솟값)을 제공할 때, 리만 합은 리만 적분과 다르부 적분(Darboux integral) 사이의 밀접한 연결을 제안하는, 위쪽 (각각, 아래) 다르부 합(Darboux sum)이 됩니다.

Lebesgue integral

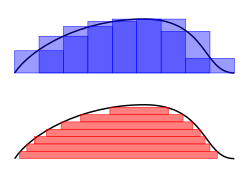
적분 아래에서 극한에 도달할 수 있는 것은, 이론 및 응용 둘 다에서, 종종 흥미롭습니다. 예를 들어, 함수의 수열은, 문제에 대한 해결책을, 적절한 의미에서, 근사화하는 것으로 자주 구성될 수 있습니다. 그런-다음 해 함수의 적분은 반드시 근사의 적분의 극한이 되어야 합니다. 어쨌든, 극한으로 얻어질 수 있는 많은 함수는 리만-적분가능이 아니고, 그래서 그러한 적분 이론은 리만 적분과 함께 유지되지 않습니다. 그러므로, 함수의 더 넓은 클래스를 적분되려는 것으로 허용하는 적분의 정의를 갖는 것이 매우 중요합니다 (Rudin 1987).

그러한 적분은 르베그 적분이며, 적분-가능한 함수의 클래스를 확대하기 위해 다음 사실을 개척합니다: 만약 함수의 값이 도메인에 걸쳐 재배열되면, 함수의 적분은 같은 것으로 유지되어야 합니다. 따라서 앙리 르베그(Henri Lebesgue)는, 폴 몽텔(Paul Montel)에게 보낸 편지에서 이렇게 이 적분을 설명하면서, 그의 이름을 낳는 적분을 도입했습니다:

나는 특정 합을 지불해야 하면, 그것은 내가 내 주머니에 모아왔던 것입니다. 나는 지폐와 동전을 주머니에서 꺼내고 내가 총액에 도달할 때까지 내가 그것을 발견한 순서에서, 그것을 채권자에게 줍니다. 이것이 리만 적분입니다. 그러나 나는 다르게 진행할 수 있습니다. 내가 주머니에서 모든 돈을 취한 후에 내가 동일한 값에 따르는 지폐와 동전을 순서화하고 그런-다음 내가 채권자에게 차례로 여러 더미(heap)를 지불합니다. 이것이 나의 적분입니다.
— Siegmund-Schultze (2008)

Folland (1984, p. 56)가 그것을 말한 것처럼, " $f$ 의 리만 적분을 계산하기 위해, 우리는 도메인 $[a, b]$ 를 부분-구간으로 분할합니다", 반면에 르베그 적분에서, "우리는 사실상 $f$ 의 범위를 분할하는 것입니다". 르베그 적분의 정의는 따라서 측정(measure), μ로 시작합니다. 가장 간단한 경우에서, 구간 $A = [a, b]$ 의 르베그 측정(Lebesgue measure) $μ (A)$ 는, 르베그 적분은, 둘 다가 존재할 때, (적절한) 리만 적분과 일치하도록, 그의 너비, $b - a$ 입니다. 보다 복잡한 경우에서, 측정되는 집합은, 연속성이 없고 구간에 대해 닮음이 없는 것과 함께, 매우 단편화될 수 있습니다.

" $f$ 의 범위를 분할하는 것" 철학을 사용하여, 비-음의 함수 $f : R \to R$ 의 적분은 반드시 $y = t$ 와 $y = t + dt$ 사이의 얇은 수평 조각 사이의 넓이의 $t$ 에 걸쳐 합이 되어야 합니다. 이 넓이는 단지 $μ {x : f (x) > t} dt$ 입니다. $f * (t) = μ {x : f (x) > t$ }라고 놓습니다. $f$ 의 르베그 적분은 그런-다음 (Lieb & Loss 2001)에 의해 정의됩니다:

\int f=\int _{0}^{\infty }f^{*}(t)\,dt

여기서 오른쪽의 적분은 보통의 부적절한 리만 적분입니다 ( $f *$ 는 엄격하게 감소하는 양의 함수이고, 그러므로 잘-정의된(well-defined) 부적절한 리만 적분을 가집니다). 함수의 적절한 클래스 (측정-가능 함수(measurable function))에 대해, 이것은 르베그 적분을 정의합니다.

일반적인 측정-가능 함수 $f$ 는, 만약 $f$ 의 그래프와 $x$ -축 사이의 영역의 절댓값의 합이 유한이면, 르베르-적분가능입니다:

\int _{E}|f|\,d\mu <+\infty .

해당 경우에서, 적분은, 리만의 경우에서 처럼, $x$ 축 위의 넓이와 $x$ 축 아래 넓이 사이의 차이입니다:

\int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu

여기서

{\begin{alignedat}{3}&f^{+}(x)&&{}={}\max\{f(x),0\}&&{}={}{\begin{cases}f(x),&{\text{if }}f(x)>0,\\0,&{\text{otherwise,}}\end{cases}}\\&f^{-}(x)&&{}={}\max\{-f(x),0\}&&{}={}{\begin{cases}-f(x),&{\text{if }}f(x)<0,\\0,&{\text{otherwise.}}\end{cases}}\end{alignedat}}

Other integrals

비록 리만 적분과 르베그 적분이 적분의 가장 널리 사용되는 정의일지라도, 많은 다른 것이 존재하고, 다음을 포함합니다:

다르부 적분(Darboux integral), 이것은 다르부 합을 사용하여 구성되고 리만 적분(Riemann integral)과 동등하며, 함수가 다르부-적분가능인 것과 그것이 리만-적분가능인 것은 필요충분 조건이라는 의미입니다. 다르부 적분은 리만 적분보다 정의하는 것이 더 간단하다는 장점이 있습니다.
리만–스틸티어스 적분(Riemann–Stieltjes integral), 리만 적분의 확장.
르베그–스틸티어스 적분(Lebesgue–Stieltjes integral), 더 나아가 요한 라돈(Johann Radon)에 의해 개발된 것으로, 이것은 리만–스틸티어스(Riemann–Stieltjes) 및 르베그 적분(Lebesgue integrals)을 일반화합니다.
대니얼 적분(Daniell integral), 이것은 측정(measure)에 대한 의존없이 르베그 적분 및 르베그–스틸티어스 적분(Lebesgue–Stieltjes integral)의 부분-합입니다.
하르 적분(Haar integral), 1933년에서 얼프레드 하르(Alfréd Haar) 에 의해 도입된, 지역적 컴팩트 토폴로지적 그룹에 대한 적분화에 사용됩니다.
헨스탁–쿠르즈베일 적분(Henstock–Kurzweil integral), 아르노 당주아(Arnaud Denjoy), 오스카 페론(Oskar Perron), 및 (가장 우아하게, 게이지 적분으로) 야로스라프 쿠르즈베일(Jaroslav Kurzweil)에 의해 다양하게 정의되고, 랄프 헨스탁(Ralph Henstock)에 의해 개발되었습니다.
이토 적분(Itô-Integral) 및 스트라토노비치 적분(Stratonovich integral), 이것은 브라운 운동(Brownian motion)과 같은 반-마턴게일(semimartingale)에 관한 적분화를 정의합니다.
영 적분(Young integral), 이것은 무경계진 변화(unbounded variation)의 특정 함수에 관한 리만–스틸티어스 적분의 종류입니다.
거친 경로(rough path) 적분, 이것은 추가적인 "거친 경로" 구조를 갖춘 함수에 대해 정의되고 분수적 브라운 운동(fractional Brownian motion)과 같은 반-마턴게일(semimartingale) 및 프로세서 둘 다에 맞서 확률론적 적분화를 일반화합니다.

Properties

Linearity

닫힌 구간 $[a, b]$ 에서 리만-적분가능 함수의 모음은 스칼라에 의한 점마다 덧셈(pointwise addition)과 곱셈의 연산 아래에서 벡터 공간(vector space)을 형성하고, 다음 적분

f\mapsto \int _{a}^{b}f(x)\;dx

의 연산은 이 벡터 공간 위에 선형 함수형(linear functional)입니다. 따라서, 첫 번째로, 적분-가능 함수의 모음은 선형 조합(linear combination)을 취하는 것 아래에 닫힙니다; 그리고, 두 번째로, 선형 조합의 적분은 그 적분의 선형 조합입니다,

\int _{a}^{b}(\alpha f+\beta g)(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx.\,

비슷하게, 측정 $μ$ 를 갖는 주어진 측정 공간(measure space) $E$ 위에 실수(real)-값 르베그-적분가능 함수의 집합은 선형 조합을 취하는 것 아래에 닫혀지고 그러므로 벡터 공간을 형성하고, 및 르베그 적분

f\mapsto \int _{E}f\,d\mu

은 다음이 되도록,

\int _{E}(\alpha f+\beta g)\,d\mu =\alpha \int _{E}f\,d\mu +\beta \int _{E}g\,d\mu

이 벡터 공간 위의 선형 함수형입니다.

보다 일반적으로, 지역적 컴팩트(locally compact) 토폴로지적 필드(topological field) $K, f : E \to V$ 에 걸쳐 지역적 컴팩트 완비(complete) 토폴로지적 벡터 공간(topological vector space) $V$ 에서 값을 취하는, 측정 공간 $(E, μ)$ 위의 모든 측정-가능 함수(measurable function)의 벡터 공간을 생각해 보십시오. 그런-다음 우리는 $V$ 의 각 함수 $f$ 원소 또는 기호 $\infty$ 를 할당하는 추상적인 적분화 맵을 다음으로 정의할 수 있습니다:

f\mapsto \int _{E}f\,d\mu ,\,

그것은 선형 조합과 호환됩니다. 이 상황에서, 선형성은 그의 적분이 $V$ 의 원소인 (즉, "유한한") 함수의 부분-공간에 대해 유지됩니다. 가장 중요한 특별한 경우는 $K$ 가 $R$ , $C$ , 또는 p-진수 숫자의 필드 $Q p$ 의 유한 확대, 및 $V$ 가 $K$ 에 걸쳐 유한-차원 벡터 공간이고, 및 $K = C$ 이고 $V$ 가 복소 힐베르트 공간(Hilbert space)일 때 발생합니다.

자연스러운 연속성 속성 및 "단순한" 함수의 특정 클래스에 대한 정규화와 함께, 선형성은 적분의 대안적인 정의를 제공하는 것에 사용될 수 있습니다. 이것은, 집합 $X$ 위의 실수-값 함수의 경우에 대해 다니엘(Daniell)의 접근법이며, 지역적으로 컴팩트 토폴로지적 벡터 공간에서 값을 갖는 함수에 대해 니콜라 부르바키(Nicolas Bourbaki)에 의해 일반화됩니다. 적분의 공리적 특성화에 대해 (Hildebrandt 1953)을 참조하십시오.

Inequalities

많은 일반적인 부등식은 닫힌(closed) 및 경계진(bounded) 구간(interval) $[a, b]$ 위에 정의된 리만-적분가능 함수(functions)에 대해 유지되고 (르베그 및 다니엘) 적분의 다른 개념으로 일반화될 수 있습니다.

위쪽 경계 및 아래쪽 경계. $[a, b]$ 위의 적분-가능 함수 $f$ 는 반드시 해당 구간 위에 필연적으로 경계진(bounded) 것입니다. 따라서 $[a, b]$ 안의 모든 $x$ 에 대해 $m \leq f (x) \leq M$ 가 되도록 실수(real) $m$ 과 $M$ 이 있습니다. 왜냐하면 $[a, b]$ 에 걸쳐 $f$ 의 아래쪽 및 위쪽 합은, 그러므로, 각각, $m (b - a)$ 및 $M (b - a)$ 에 의해 경계지며, 그것은 다음임을 따릅니다:

m(b-a)\leq \int _{a}^{b}f(x)\,dx\leq M(b-a).

함수들 사이의 부등식. 만약 $[a, b]$ 안의 각 $x$ 에 대해 $f (x) \leq g (x)$ 이면, $f$ 의 위쪽 및 아래쪽 합의 각각은 $g$ 의, 각각, 위쪽 합과 및 아래쪽 합에 의해 위로 경계집니다. 따라서

\int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)\,dx.

이것은 위의 부등식의 일반화인데, 왜냐하면

M (b - a)

는

[a, b]

에 걸쳐 값

M

을 갖는 상수 함수의 적분이기 때문입니다.

게다가, 만약 함수 사이의 부등식이 엄격하면, 적분 사이의 부등식은 역시 엄격합니다. 즉, 만약

[a, b]

안의 각

x

에 대해

f (x) < g (x)

이면, 다음입니다:

\int _{a}^{b}f(x)\,dx<\int _{a}^{b}g(x)\,dx.

부분-구간. 만약 $[c, d]$ 가 $[a, b]$ 의 부분-구간이고 $f (x)$ 가 모든 $x$ 에 대해 비-음수이면, 다음입니다:

\int _{c}^{d}f(x)\,dx\leq \int _{a}^{b}f(x)\,dx.

곱 및 함수의 절댓값. 만약 $f$ 와 $g$ 가 두 함수이면, 우리는 그들의 점마다 곱(pointwise product)과 거듭제곱, 및 절댓값(absolute value)을 고려할 수 있습니다:

(fg)(x)=f(x)g(x),\;f^{2}(x)=(f(x))^{2},\;|f|(x)=|f(x)|.\,

만약

f

가

[a, b]

위에 리만-적분가능이면, 같은 것은

| f |

에 대해 참이고, 다음입니다:

\left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx.

게다가, 만약

f

와

g

가 둘 다 리만-적분가능이면,

fg

는 역시 리만-적분가능이고, 다음입니다:

\left(\int _{a}^{b}(fg)(x)\,dx\right)^{2}\leq \left(\int _{a}^{b}f(x)^{2}\,dx\right)\left(\int _{a}^{b}g(x)^{2}\,dx\right).

코시–슈바르츠 부등식(Cauchy–Schwarz inequality)으로 알려진, 이 부등식은 힐베르트 공간(Hilbert space) 이론에서 두드러진 역할을 하며, 여기서 왼쪽 편은 구간

[a, b]

위의 두 제곱-적분가능(square-integrable) 함수

f

와

g

의 안의 곱(inner product)으로 해석됩니다.

휠더의 부등식. $p$ 와 $q$ 가, $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:.0 .1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:.1em .1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0 0,0 0,0 0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/p + 1/q = 1$ 을 갖는 $1 \leq p, q \leq \infty$ 인, 두 실수이고, $f$ 와 $g$ 는 두 리만-적분가능 함수라고 가정합니다. 그런-다음 함수 $| f | p$ 와 $| g | q$ 는 역시 적분-가능이고 다음 휠더의 부등식(Hölder's inequality)이 유지됩니다:

\left|\int f(x)g(x)\,dx\right|\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}\left(\int \left|g(x)\right|^{q}\,dx\right)^{1/q}.

p

=

q

= 2에 대해, 휠더의 부등식은 코시-슈바르츠 부등식이 됩니다.

민코프스키 부등식. $p \geq 1$ 가 실수이고 $f$ 와 $g$ 가 리만-적분가능 함수로 가정합니다. 그런-다음 $| f | p, | g | p$ 및 $| f + g | p$ 는 역시 리만-적분가능이고 다음 민코프스키 부등식(Minkowski inequality)이 유지됩니다:

\left(\int \left|f(x)+g(x)\right|^{p}\,dx\right)^{1/p}\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}+\left(\int \left|g(x)\right|^{p}\,dx\right)^{1/p}.

르베그 적분에 대해 이러한 부등식의 아날로그는 L^p 공간의 구성에서 사용됩니다.

Conventions

이 섹션에서, $f$ 는 실수(real)-값 리만-적분가능 함수(function)입니다. 구간 $[a, b]$ 에 걸친 적분

\int _{a}^{b}f(x)\,dx

은 만약 $a < b$ 이면 정의됩니다. 이것은, 함수 $f$ 의 위쪽 및 아래쪽 합이 그의 값 $x i$ 가 증가하는 것에서 분할 $a = x 0 \leq x 1 \leq . . . \leq x n = b$ 에 대해 평가된다는 것을 의미합니다. 기하학적으로, 이것은 적분화가 "왼쪽에서 오른쪽"으로 자리를 차지함을 의미하며, 구간 $[x i, x i +1]$ 이내인 $f$ 를 평가하는 것으로, 여기서 더 높은 인덱스를 갖는 구간은 더 낮은 인덱스를 갖는 구간의 오른쪽에 놓입니다. 구간(interval)의 끝-점, 값 $a$ 와 $b$ 는 $f$ 의 적분화의 극한(limits of integration)으로 불립니다. 적분은 만약 $a > b$ 이면 다음으로 역시 정의될 수 있습니다:

적분화의 거꾸로 뒤집는 극한. 만약 $a > b$ 이면 다음을 정의합니다:

\int _{a}^{b}f(x)\,dx=-\int _{b}^{a}f(x)\,dx.

이것은, $a = b$ 와 함께, 다음을 의미합니다:

길이 영의 구간에 걸쳐 적분. 만약 $a$ 가 실수(real)이면, 다음입니다:

\int _{a}^{a}f(x)\,dx=0.

첫 번째 관례는 $[a, b]$ 의 부분-구간에 걸친 적분을 취하는 것의 고려에서 필요합니다; 두 번째는 퇴화 구간(degenerate interval) 또는 점(point)에 걸쳐 취해진 적분은 반드시 영(zero)이어야 한다고 말합니다. 첫 번째 관례에 대한 하나의 이유는 구간 $[a, b]$ 위의 $f$ 의 적분-가능성은 $f$ 가 임의의 부분-구간 $[c, d]$ 에서 적분-가능하다는 것을 의미하지만, 특히 적분은 다음과 같은 속성을 가집니다:

구간에 대한 적분화의 덧셈성. 만약 $c$ 가 $[a, b]$ 의 임의의 원소(element)이면, 다음입니다:

\int _{a}^{b}f(x)\,dx=\int _{a}^{c}f(x)\,dx+\int _{c}^{b}f(x)\,dx.

첫 번째 관례와 함께, 결과 관계

{\begin{aligned}\int _{a}^{c}f(x)\,dx&{}=\int _{a}^{b}f(x)\,dx-\int _{c}^{b}f(x)\,dx\\&{}=\int _{a}^{b}f(x)\,dx+\int _{b}^{c}f(x)\,dx\end{aligned}}

는 $a$ , $b$ , 및 $c$ 의 임의의 순환 순열에 대해 잘-정의됩니다.

Fundamental theorem of calculus

미적분학의 기본 정리는 미분화와 적분화는 역 연산이라는 명제입니다: 만약 연속 함수(continuous function)가 먼저 적분되고 그런-다음 미분되면, 원래 함수가 구해집니다. 때때로 미적분학의 두 번째 기본 정리로 불리는, 중요한 결과는 우리에게 적분되어지는 함수의 역도함수를 사용함으로써 적분을 계산하는 것을 허용합니다.

Statements of theorems

Fundamental theorem of calculus

$f$ 를 닫힌 구간(closed interval) $[a, b]$ 위에 정의된 연속 실수-값 함수로 놓습니다. $F$ 를, $[a, b]$ 안의 모든 $x$ 에 대해, 다음에 의해 정의된 함수로 놓습니다:

F(x)=\int _{a}^{x}f(t)\,dt.

그런-다음, $F$ 는 $[a, b]$ 위에 연속이고, 열린 구간 $(a, b)$ 위에 미분-가능이고, $(a, b)$ 안의 모든 $x$ 에 대해 다음입니다:

F'(x)=f(x)

.

Second fundamental theorem of calculus

$f$ 를 $[a, b]$ 위에 역도함수(antiderivative) $F$ 를 허용하는 닫힌 구간(closed interval) [ $a, b$ ] 위에 정의된 실수-값 함수로 놓습니다. 즉, $f$ 와 $F$ 는 $[a, b]$ 안의 모든 $x$ 에 대해 다음을 만족하는 함수입니다:

f(x)=F'(x).

만약 $f$ 는 $[a, b]$ 위에 적분-가능이면,

\int _{a}^{b}f(x)\,dx=F(b)-F(a).

Calculating integrals

두 번째 기본 정리는 명시적으로 계산될 수 있는 많은 적분을 허용합니다. 예를 들어, 0과 1 사이에 제곱근 함수 $f (x) = x 1/2$ 의 다음 적분을 계산하기 위해

\int _{0}^{1}x^{1/2}\,dx,

역도함수, 즉 그의 도함수가 $f (x)$ 와 같은 함수 $F (x)$ 를 찾는 것으로 충분합니다:

F'(x)=f(x).

하나의 그러한 함수는 $F(x)={\tfrac {2}{3}}x^{3/2}$ 입니다. 그런-다음 질문에서 적분의 값은 다음입니다:

\int _{0}^{1}x^{1/2}\,dx\ =\ F(1)-F(0)\ =\ {\tfrac {2}{3}}(1)^{3/2}-{\tfrac {2}{3}}(0)^{3/2}\ =\ {\tfrac {2}{3}}.

이것은 $q\neq 1$ 를 갖는, $f(x)=x^{q}$ 에 대해, 역도함수가 $F(x)={\tfrac {1}{q+1}}x^{q+1}$ 인, 일반적인 규칙의 경우입니다. 이것과 유사한 역도함수의 테이블은 명시적으로 적분을 계산하기 위해 사용될 수 있으며, 많은 같은 방법에서 해당 도함수는 테이블로부터 얻어질 수 있을 것입니다.

Extensions

Improper integrals

"적절한" 리만 적분은, 피적분이 정의되고 적분의 극한에 의해 괄호로 묶이는, 닫힌 및 경계진 구간 위에 유한하다고 가정합니다. 부적절한 적분은 이들 조건 중 하나 이상이 만족되지 않을 때 발생합니다. 어떤 경우에서, 그러한 적분은 점차적으로 더 큰 구간 위에 적절한 리만 적분(Riemann integral)의 수열(sequence)의 극한(limit)을 고려함으로써 정의될 수 있을 것입니다.

만약 구간이, 예를 들어 그의 위쪽 끝에서, 무경계이면, 부적절한 적분은 해당 끝점이 무한대로 갈 때 극한입니다.

\int _{a}^{\infty }f(x)\,dx=\lim _{b\to \infty }\int _{a}^{b}f(x)\,dx

만약 피적분이 오직 정의되는 것 또는, 예를 들어 $(a, b]$ 처럼, 반-열린 구간 위에 유한이면, 다시 극한은 유한 결과를 제공할 수 있을 것입니다.

\int _{a}^{b}f(x)\,dx=\lim _{\varepsilon \to 0}\int _{a+\epsilon }^{b}f(x)\,dx

즉, 부적절한 적분은 적분화의 구간의 한 끝점이 지정된 실수(real), 또는 $\infty$ , 또는 $-\infty$ 중의 하나에 접근할 때 적절한 적분의 극한(limit)입니다. 보다 복잡한 경우에서, 극한은 양쪽 끝점 둘 다, 또는 내부 점에 요구됩니다.

Multiple integration

단지 한 변수의 양의 함수의 한정 적분은 함수의 그래프와 x-축 사이의 영역의 넓이(area)를 나타내는 것처럼, 두 변수의 양의 함수의 이중 적분(double integral)은 함수에 의해 정의된 표면과 그의 도메인(domain)을 포함하는 평면 사이의 영역의 부피(volume)를 나타냅니다. 예를 들어, 이 차원에서 함수는 두 실수 변수, x와 y에 의존하고, 두 구간의 데카르트 곱(Cartesian product) $R=[a,b]\times [c,d]$ 으로 주어진 직사각형 R에 걸쳐 함수 f의 적분은 다음으로 쓸 수 있습니다:

\int _{R}f(x,y)\,dA

여기서 미분 $dA$ 는 적분화가 넓이에 관해 취해짐을 나타냅니다. 이 이중 적분(double integral)은 리만 합(Riemann sum)을 사용하여 정의될 수 있고, 도메인 R에 걸쳐 $z = f (x, y)$ 의 그래프 아래의 (부호화된) 부피를 나타냅니다. 적절한 조건 (예를 들어, f가 연속이면) 아래에서, 푸비니의 정리(Fubini's theorem)는 이 적분이 다음의 동등한 반복된 적분으로 표현될 수 있음을 말합니다:

\int _{a}^{b}\left[\int _{c}^{d}f(x,y)\,dy\right]\,dx.

이것은 이중 적분을 계산하는 문제를 일-차원 적분을 계산하는 것으로 줄입니다. 이것 때문에, R에 걸친 적분에 대해 또 다른 표기법은 이중 적분 기호를 사용합니다:

\iint _{R}f(x,y)\,dA.

보다 일반적인 도메인에 걸친 적분화가 가능합니다. $\mathbb {R} ^{n}$ 의 n-차원 영역 D에 걸쳐, 부피의 관한, 함수 f의 적분은 다음에서 처럼 기호에 의해 표시됩니다:

\int _{D}f(\mathbf {x} )d^{n}\mathbf {x} \ =\int _{D}f\,dV.

Line integrals

적분의 개념은, 구부러진 선 및 고차원 공간 내부의 표면과 같은, 적분화의 보다 일반적인 도메인으로 확장될 수 있습니다. 그러한 적분은, 각각, 곡선 적분 및 표면 적분으로 알려져 있습니다. 이들은, 벡터 필드(vector field)를 다룰 때처럼, 물리학에서 중요한 응용을 가집니다.

곡선 적분(line integral) (때때로 경로 적분(path integral)으로 불림)은 적분되려는 함수(function)가 곡선(curve)을 따라 평가되는 적분입니다. 다양한 다른 곡선 적분이 사용됩니다. 닫힌 곡선의 경우에서, 이를 윤곽 적분(contour integral)으로 역시 불립니다.

적분되려는 함수는 스칼라 필드(scalar field) 또는 벡터 필드(vector field)일 수 있습니다. 곡선 적분의 값은 곡선 위의 모든 점에서 필드의 값의 합이며, 곡선 위의 어떤 스칼라 함수로 가중됩니다 (공통적으로 호 길이(arc length), 또는 벡터 필드에 대해, 곡선에서 미분(differential) 벡터를 갖는 벡터 필드의 스칼라 곱(scalar product)). 이 가중하는 것은 구간(interval) 위에 정의된 더 단순한 적분으로부터 곡선 적분을 구별합니다. 물리학에서 많은 간단한 공식은 곡선 적분의 관점에서 자연스러운 연속 아날로그를 가집니다; 예를 들어, 일(work)이, 변위, $s$ 에 의해 곱해진, 힘(force), $F$ 와 같다는 사실은 다음으로 (벡터 양의 관점에서) 표현될 수 있을 것입니다:

W=\mathbf {F} \cdot \mathbf {s} .

전기 필드(electric field) 또는 중력 필드(gravitational field)와 같은, 벡터 필드(vector field) $F$ 에서 경로 $C$ 를 따라 움직이는 물체에 대해, 물체 위의 필드에 의해 행해진 전체 일은 $s$ 에서 $s + d s$ 까지 이동하는 것에서 행해진 미분 일을 합함으로써 구해집니다. 이것은 다음 곡선 적분을 제공합니다:

W=\int _{C}\mathbf {F} \cdot d\mathbf {s} .

Surface integrals

표면 적분(surface integral)은 표면(surface)에 걸쳐 적분화에 대한 이중 적분입니다 (표면은 공간에서 곡선 집합일 수 있습니다); 그것은 곡선 적분(line integral)의 이중 적분(double integral) 아날로그로 생각될 수 있습니다. 적분되려는 함수는 스칼라 필드(scalar field) 또는 벡터 필드(vector field)일 수 있습니다. 표면 적분의 값은 표면 위의 모든 점에서 필드의 합입니다. 이것은 표면을 표면 원소로 분리함으로써 달성될 수 있으며, 이것은 리만 합에 대해 분할하는 것을 제공합니다.

표면 적분의 응용의 예제에 대해, 표면 $S$ 위의 벡터 필드 $v$ 를 생각해 보십시오; 즉, $S$ 안의 각 점 $x$ 에 대해, $v (x)$ 는 벡터입니다. $v (x)$ 가 $x$ 에서 유체의 속도를 결정하는 것을 만족하는, $S$ 를 통해 흐르는 유체를 상상해 보십시오. 선속도(flux)는 시간의 총 단위에서 $S$ 를 통해 흐르는 유체의 양으로 정의됩니다. 선속도를 구하기 위해, 우리는 각 점에서 $S$ 에 대한 단위 표면 수직(surface normal)을 갖는 $v$ 의 점 곱(dot product)을 취할 필요가 있으며, 이것은 우리에게 스칼라 필드를 제공하며, 우리가 이것을 표면에 걸쳐 적분됩니다:

\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }.

유체 선속도는 이 예제에서 물 또는 공기와 같은 물리적 유체, 또는 전기적 또는 자기적 유체으로부터 될 수 있습니다. 따라서 표면 적분은 물리학, 특히 전자기학(electromagnetism)의 고전 이론(classical theory)과 함께 응용을 가집니다.

Contour integrals

복소 해석학에서, 피적분은 실수 변수 $x$ 의 실수 함수 대신에 복소수 변수 $z$ 의 복소수-값 함수(complex-valued function)입니다. 복소 함수가 복소 평면에서 곡선 $\gamma$ 를 따라 적분될 때, 적분은 다음으로 표시됩니다:

\int _{\gamma }f(z)\,dz.

이것은 윤곽 적분(contour integral)으로 알려져 있습니다.

Integrals of differential forms

미분 형식(differential form)은 다변수 미적분학(multivariable calculus), 미분 토폴로지(differential topology) 및 텐서(tensor)의 분야에서 수학적 개념입니다. 미분 형식은 차수에 의해 구성됩니다. 예를 들어, 일-형식은, 다음에서 처럼, 좌표의 미분의 가중화된 합입니다:

E(x,y,z)\,dx+F(x,y,z)\,dy+G(x,y,z)\,dz

여기서 E, F, G는 삼 차원에서 함수입니다. 미분 일-형식은 지향된 경로에 걸쳐 적분될 수 있고, 결과 적분은 곡선 적분을 작성하는 단지 또 다른 방법입니다. 여기서 기본 미분 dx, dy, dz는 세 좌표축에 평행한 무한소 방향화된 길이를 측정합니다.

미분 이-형식은 다음 형식의 합입니다:

G(x,y,z)\,dx\wedge dy+E(x,y,z)\,dy\wedge dz+F(x,y,z)\,dz\wedge dx.

여기서 기본 이-형식 $dx\wedge dy,dz\wedge dx,dy\wedge dz$ 은 좌표 두-평면에 평행한 방향화된 넓이를 측정합니다. 기호 $\wedge$ 는 쐐기 곱(wedge product)을 나타내며, 이것은 방향화된 길이를 나타내는 이-형식의 쐐기 곱은 방향화된 넓이를 나타내는 것이라는 의미에서 교차 곱(cross product)과 비슷합니다. 이-형식은 방향화된 표면에 걸쳐 적분될 수 있고, 결과 적분은 $E\mathbf {i} +F\mathbf {j} +G\mathbf {k}$ 의 선속도를 제공하는 표면 적분과 동등합니다.

교차 곱 및 삼-차원 벡터 미적분과는 달리, 쐐기 곱 및 미분 형식의 미적분은 임의의 차원에서 및 보다 일반적인 매니폴드 (곡선, 곡면, 및 그들의 고차원 아날로그) 위에 의미를 만듭니다. 외부 도함수(exterior derivative)는 벡터 미적분의 그래디언트(gradient)와 컬(curl)의 역할을 하고, 스토크스의 정리(Stokes' theorem)는 벡터 미적분학의 세 가지 정리: 발산 정리(divergence theorem), 그린의 정리(Green's theorem) 및 켈빈-스토크스 정리(Kelvin-Stokes theorem)를 동시에 일반화합니다.

Summations

적분의 이산 등가는 합계(summation)입니다. 합계와 적분은 르베그 적분(Lebesgue integral) 또는 시간 스케일 미적분학(time scale calculus)의 이론을 사용하여 같은 토대 위에 놓일 수 있습니다.

Computation

Analytical

한 실수 변수의 한정 적분을 계산하는 것에 대해 가장 기본 기법은 미적분학의 기본 정리(fundamental theorem of calculus)에 기초합니다. $f (x)$ 를 주어진 구간 $[a, b]$ 에 걸쳐 적분되려는 $x$ 의 함수로 놓습니다. 그런-다음, $f$ 의 역도함수(antiderivative); 즉, 구간 위에 $F' = f$ 을 만족하는 함수 $F$ 를 찾으십시오. 피적분과 적분이 적분화의 경로 위에 특이성(singularities)을 가지지 않는 것으로 제공되면, 미적분의 기본 정리에 의해,

\int _{a}^{b}f(x)\,dx=F(b)-F(a).

적분은 실제적으로 역도함수는 아니지만, 기본 정리는 한정 적분을 평가하기 위해 역도함수를 사용하기 위한 방법을 제공합니다.

가장 어려운 단계는 보통 $f$ 의 역도함수를 찾는 것입니다. 함수를 한눈에 파악하고 그의 역도함수를 쓰는 것은 거의 불가능합니다. 보다 자주, 적분을 평가하기 위해 개발되어 온 많은 기법 중 하나를 사용해야 합니다. 이들 기법의 대부분은 희망적으로 보다 다루기 쉬운 다른 것으로 하나의 적분을 재작성합니다. 기법은 다음을 포함합니다:

대안적인 방법은 보다 복잡한 적분을 계산하기 위해 존재합니다. 많은 비-기본 적분(nonlementary integrals)은 테일러 급수(Taylor series)에 의해 전개되고 항별로 적분될 수 있습니다. 때때로, 결과 무한 급수는 해석적으로 합해질 수 있습니다. 마이어 G-함수(Meijer G-function)를 사용하여 합성곱의 방법은 역시 사용될 수 있으며, 피적분은 마이어 G-함수의 곱으로 쓸 수 있다는 것을 가정합니다. 한정 적분을 계산하는 것의 많은 덜 공통적인 방법이 역시 있습니다; 예를 들어, 파서반의 항등식(Parseval's identity)은 직사각형 영역에 걸쳐 적분을 무한 합으로 변환하기 위해 사용될 수 있습니다. 때때로, 적분은 트릭에 의해 평가될 수 있습니다; 이것의 예제에 대해, 가우스 적분(Gaussian integral)을 참조하십시오.

회전 고체(solids of revolution)의 부피의 계산은 보통 디스크 적분화(disk integration) 또는 쉘 적분화(shell integration)와 함께 수행될 수 있습니다.

다양한 기법에 의해 연구되어 왔던 특정 결과는 적분의 목록(list of integrals)에 모여져 있습니다.

Symbolic

수학, 물리학 및 공학에서 많은 문제는 적분에 대한 명시적인 공식이 희망되는 적분화를 포함합니다. 광범위한 적분의 테이블(tables of integrals)은 이 목적에 대해 수년에 걸쳐 수집 및 게시되어 왔습니다. 컴퓨터가 보급과 함께, 많은 전문가, 교육자, 및 학생이 적분화를 포함하는 어렵거나 지루한 태스크를 수행하기 위해 특별히 설계된 컴퓨터 대수학 시스템(computer algebra system)으로 방향을 바꾸어 왔습니다. 기호적인 적분은 맥시마(Macsyma)와 같은 최초의 그런 시스템 개발에 대해 동기 중 하나였습니다.

기호적 적분화에서 주요 수학적 어려움은 많은 경우에서, 꽤 단순해-보이는 함수의 역도함수에 대해 닫힌 공식이 존재하지 않는다는 것입니다. 예를 들어, 함수 $exp(x 2), x x$ 및 $(sin x)/ x$ 의 역도함수는 오직 유리 (rational) 및 지수 함수(exponential function), 로그(logarithm), 삼각 함수(trigonometric functions) 및 역 삼각 함수(inverse trigonometric functions), 및 곱셈과 합성의 연산을 포함하는 닫힌 형식으로 절대 표현될 수 없는 것으로 알려져 있습니다; 다른 말로, 세 개의 주어진 함수 중 어느 것도, 유리 함수, 다항식의 근, 로그, 및 지수 함수로부터 만들어질 수 있는 함수인, 초등 함수(elementary function)에서 적분-가능하지 않습니다. 리시 알고리듬(Risch algorithm)은 초등 함수의 역도함수가 기본적인지 여부를 결정하기 위한 일반적인 기준을 제공하고, 만약 그렇다면, 그것을 계산하기 위한 것입니다. 불행하게도, 역도함수의 닫힌 표현을 가진 함수는 규칙이 아니라 예외인 것으로 밝혀집니다. 결과적으로, 컴퓨터화 대수학 시스템은 확률적으로 구성된 초등 함수에 대해 역도함수를 찾을 수 있는 희망이 없습니다. 긍정적인 측면에서, 만약 역도함수에 대한 '빌딩 블록(building blocks)'이 미리 고정되면, 주어진 함수의 역도함수가 이들 블록과 곱셈과 합성의 연산을 사용하여 표현될 수 있는지 여부를 결정하는 것, 및 그것이 존재할 때마다 기호적인 답을 찾기 위한 것이 여전히 가능할 수 있습니다. 매스매티카(Mathematica) 및 다른 컴퓨터 대수학 시스템(computer algebra system)에서 구현된, 리시 알고리듬(Risch algorithm)은 유리 함수, 제곱근(radicals), 로그, 및 지수 함수로부터 만들어진 함수와 역도함수에 대해 단지 수행합니다.

일부 특별한 피적분은 종종 특별 연구를 충족하기에 충분합니다. 특히, 역도함수의 집합에서, 특수 함수(special functions)를 갖기 위해서 유용될 수 있습니다 (르장드르 함수(Legendre function), 초기하학 함수(hypergeometric function), 감마 함수(gamma function), 불완전한 감마 함수(incomplete gamma function), 등등 — 자세한 내용은 기호적 적분화(Symbolic integration)를 참조하십시오). 그러한 함수를 포함하기 위한 리시의 알고리듬을 확장하는 것은 가능하지만 도전적인 것이고 활동적인 연구 주제를 가져왔습니다.

보다 최근 새로운 접근은, D-유한 함수(D-finite functions)를 사용하여, 등장해 왔으며, 이것은 다항 계수를 갖는 선형 미분 방정식(linear differential equation)의 해입니다. 초등 함수와 특수 함수의 대부분은 D-유한이고, D-유한 함수의 적분은 역시 D-유한 함수입니다. 이것은 D-유한 함수의 역도함수를 미분 방정식의 해로 표현하기 위한 알고리듬을 제공합니다.

이 이론은 역시 우리에게 첫 번째 계수에 의해 주어진 급수의 합으로서 D-함수의 한정 적분을 계산하는 것을 허용하고, 임의의 계수를 계산하기 위해서 알고리듬을 제공합니다.^[5]

Numerical

실수 응용에서 발견된 일부 적분은 닫힌-형식 역도함수에 의해 계산될 수 있습니다. 다른 것들은 그렇게 수용하지 못합니다. 일부 역도함수는 닫힌-형식을 가지지 못하고, 일부 닫힌-형식은 그들 자신이 계산하기 위해서 도전을 해야 하는 특수 함수를 요구하고, 다른 것들은 너무 복잡해서 정확한 대답을 찾는 것이 너무 느립니다. 이것은 적분의 수치적 근사의 연구와 응용을 동기-부여합니다. 수치적 적분화(numerical integration) 또는 수치적 구적법(numerical quadrature)으로 불리는 이 주제는 손 계산을 하기 위한 목적으로 적분화의 연구에서 초기에 나타났습니다. 일반적인-목적 컴퓨터의 개발은 수치적 적분화를 보다 실용적으로 만들고 개선에 대해 희망을 불어 넣었습니다. 수치적 적분화의 목표는 정확성, 신뢰성, 효율성, 및 보편성이고, 정교한 현대적 방법은 네 가지 방법 모두에 의해 소박한 방법보다 월등히 뛰어날 수 있습니다 (Dahlquist & Björck 2008; Kahaner, Moler & Nash 1989; Stoer & Bulirsch 2002).

다음 적분을, 예를 들어, 생각해 보십시오:

\int _{-2}^{2}{\tfrac {1}{5}}\left({\tfrac {1}{100}}(322+3x(98+x(37+x)))-24{\frac {x}{1+x^{2}}}\right)dx

이것은 정확한 답 94/25 = 3.76을 가집니다. (보통의 연습에서, 답이 미리 알려지지 않으므로, 중요한 임무 — 여기서 탐구하지 않습니다 —는 근사가 충분히 좋을 때를 결정하는 것입니다.) "미적분학 책"은 적분화 범위를, 말하자면, 16 등분으로 나누고, 함수 값을 계산합니다.

Spaced function values
x	−2.00		−1.50		−1.00		−0.50		0.00		0.50		1.00		1.50		2.00
f(x)	2.22800		2.45663		2.67200		2.32475		0.64400		−0.92575		−0.94000		−0.16963		0.83600
x		−1.75		−1.25		−0.75		−0.25		0.25		0.75		1.25		1.75
f(x)		2.33041		2.58562		2.62934		1.64019		−0.32444		−1.09159		−0.60387		0.31734

각 조각의 왼쪽 끝을 사용하면, 사각형 방법(rectangle method)은 16 함수 값을 합하고 단계 폭, $h$ , 여기서 0.25에 의해 곱해지고, 적분에 대해 3.94325의 근사를 얻는 것입니다. 정확도는 인상적이지는 않지만, 미적분학은 공식적으로 무한소 너비의 조각을 사용하므로, 초기에 이것은 걱정할 필요가 없는 것 같을 것입니다. 실제로, 반복적으로 단계의 숫자를 두 배로 늘리는 것은 3.76001의 근사를 생성합니다. 어쨌든, 2¹⁸ 조각이 요구되며, 그런 낮은 정밀도에 대해 엄청난 계산 비용이 듭니다; 그리고 더 큰 정확도를 위한 도달은 작은 단계를 강제하므로 산술 정밀도가 장애가 됩니다.

더 나은 접근은 사다리꼴과 함께 리만 합에서 사용된 직사각형을 대체합니다. 사다리꼴 규칙(trapezoid rule)은 거의 계산하는 것이 쉽습니다; 그것은 모든 17 함수 값을 합하지만, 처음과 마지막을 절반으로 가중하고, 다시 단계 너비에 의해 곱해집니다. 이것은 즉각적으로 3.76925로 근사를 개선하며, 이것은 눈에 띄게 더 정확합니다. 게다가, 오직 2¹⁰ 조각이 3.76000을 달성하기 위해 필요되며, 비교 정확도에 대해 직사각형 방법보다 대체로 적은 계산을 요구합니다. 함수에 대한 보다 정확한 근사가 적분에 대한 더 나은 근사를 산출하는, 사다리꼴 규칙의 숨은 아이디어는 더 나아가서 수반될 수 있습니다. 심슨의 규칙(Simpson's rule)은 조각별 이차 함수에 의해 피적분을 근사화합니다. 리만 합, 사다리꼴 규칙, 및 심슨의 규칙은 뉴턴–코츠 공식(Newton–Cotes formulas)으로 불리는 구적법 규칙의 가족의 예제입니다. 차수 $n$ 뉴턴–코츠 구적법 규칙은 차수 $n$ 다항식에 의해 각 부분-구간 위에 다항식을 근사화합니다. 이 다항식은 구간 위에 함수의 값을 보간하기 위해 선택됩니다. 더 높은 차수의 뉴턴-코츠 근사는 더 정확할 수 있지만, 그들은 더 많은 함수 평가를 요구하고 (이미 심슨의 규칙은 사다리꼴 규칙의 두 배의 함수 평가를 요구합니다), 그들은 룽게의 현상(Runge's phenomenon)으로 기인한 수치적 부정확성으로 인해 어려움을 겪을 수 있습니다. 이 문제에 대한 한 가지 해결책은 클렌쇼–커티스 구적법(Clenshaw–Curtis quadrature)이며, 그것에서 피적분은 체비쇼프 다항식(Chebyshev polynomials)의 관점에서 그것을 확장함으로써 근사화됩니다. 이것은 그의 값이 원래 함수의 값으로부터 멀리 벗어나지 않는 근사를 생성합니다.

롬베르크의 방법(Romberg's method)은 사다리꼴 방법을 바탕으로 큰 효과를 냅니다. 첫 번째, 단계 길이는 점진적으로 절반으로 감소하여, $T (h 0), T (h 1)$ , 등등의 사다리꼴 근사를 얻으며, 여기서 $h k +1$ 은 $h k$ 의 절반입니다. 각각의 새로운 단계 크기에 대해, 오직 새로운 함수 값 절반이 계산이 필요합니다; (위의 테이블에서 보이는 것처럼) 다른 것은 이전 크기에서 이월됩니다. 그러나 정말로 강력한 아이디어는 근사를 통해 다항식을 보간하는 것이고, $T (0)$ 에 대해 외삽하는 것입니다. 이 방법과 함께 수치적으로 정확한 답은 오직 네 조각 (다섯 함수 값)을 여기서 요구합니다. ${h k, T (h k)} k = 0...2 =$ {(4.00,6.128), (2.00,4.352), (1.00,3.908)}을 보간하는 라그랑주 다항식(Lagrange polynomial)은 3.76 + 0.148 $h 2$ 이며, $h = 0$ 에서 외삽된 값 3.76을 생성합니다.

가우스 구적법(Gaussian quadrature)은 종종 우수한 정확도에 대해 두드러지게 적은 작업을 요구합니다. 이 예제에서, 그것은 단지 두 $x$ 위치, $\pm2 ⁄ \sqrt 3$ 에서 함수 값을 계산할 수 있으며, 그런-다음 각 값을 두 배로 하고 수치적으로 정확한 답을 얻기 위해서 합합니다. 이 극적인 성공에 대한 설명은 점의 선택에 달려 있습니다. 고르게 간격된 점에서 피적분을 보간하는, 뉴턴-코츠 규칙과는 달리, 가우스 구적법은 직교 다항식(orthogonal polynomials)의 집합의 근에서 함수를 평가합니다. $n$ -점 가우스 방법은 $2 n - 1$ 까지 차수의 다항식에 대해 정확합니다. 함수는 이 예제에서 차수 3 다항식이고, 취소되는 하나의 항을 더하는데 왜냐하면 선택된 끝점이 0을 주위에서 대칭이기 때문입니다. (취소는 롬베르크 방법에 역시 도움이 됩니다.)

연습에서, 각 방법은 알려지지-않은 함수에 대한 오류 경계를 보장하기 위해 여분의 평가를 반드시 사용해야 합니다; 이것은 순수한 가우스 방법의 장점 중 일부를 상쇄하는 경향이 있고, 인기있는 가우스–크론로드 구적법 공식(Gauss–Kronrod quadrature formula)을 동기-부여합니다. 보다 광범위하게, 적응 구적법(adaptive quadrature)은, 데이터 점들은 그들이 가장 필요한 곳에 집중되도록, 함수 속성에 기초한 범위로 조각을 분할합니다.

고-차원 적분의 계산 (예를 들어, 부피 계산)은 몬테 카를로 적분화(Monte Carlo integration)와 같은 그러한 대안의 중요한 사용을 만듭니다.

미적분학 텍스트가 수치적 해석학에 대해 대체할 수 없지만, 그 반대도 역시 참입니다. 비록 가장 적응 수치적 코드가 때때로 보다 까다로운 적분과 함께 사용자에게 도울 것을 요구합니다. 예를 들어, 부적절한 적분은 무한 함수 값을 피할 수 있는 변수 또는 방법의 변경이 필요할 수 있고, 대칭 및 주기성과 같은 알려진 속성은 결정적인 이점을 제공할 수 있습니다. 예를 들어, 적분 $\int _{0}^{1}x^{-1/2}e^{-x}\,dx$ 은 수치적으로 평가하기 어려운데, 왜냐하면 그것은 $x = 0$ 에서 무한하기 때문입니다. 어쨌든, 치환 $u = \sqrt x$ 은 적분을 $2\int _{0}^{1}e^{-u^{2}}\,du$ 로 변환하며, 이것은 더이상 특이점을 가지지 않습니다.

Mechanical

임의의 이-차원 형상의 넓이는 플래니미터(planimeter)로 불리는 측정하는 기구를 사용하여 결정될 수 있습니다. 불규칙한 물체의 부피는 물체가 잠김에 따라 변위된(displaced) 유체에 의해 정밀과 함께 측정될 수 있습니다.

Geometrical

넓이는 때때로 동등한 정사각형(square)의 기하학적(geometrical) 컴퍼스-와-직선자 구조(compass-and-straightedge construction)를 통해 발견될 수 있습니다.

References

^ Katz, V.J. 1995. "Ideas of Calculus in Islam and India." Mathematics Magazine (Mathematical Association of America), 68(3):163–174.
^ In the 20th century, nonstandard analysis was developed as a new approach to calculus that incorporates a rigorous concept of infinitesimals by using an expanded number system called the hyperreal numbers. Though placed on a sound axiomatic footing and of interest in its own right as a new area of investigation, nonstandard analysis remains somewhat controversial from a pedagogical standpoint, with proponents pointing out the intuitive nature of infinitesimals for beginning students of calculus and opponents criticizing the logical complexity of the system as a whole.
^ (W3C 2006).
^ Weisstein, Eric W. "Riemann Sum". MathWorld.
^ Frédéric Chyzak's Mgfun Project: Introduction to the Package Mgfun and Related Packages

Bibliography

Apostol, Tom M. (1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1
Bourbaki, Nicolas (2004), Integration I, Springer Verlag, ISBN 3-540-41129-1. In particular chapters III and IV.
Burton, David M. (2005), The History of Mathematics: An Introduction (6th ed.), McGraw-Hill, p. 359, ISBN 978-0-07-305189-5
Cajori, Florian (1929), A History Of Mathematical Notations Volume II, Open Court Publishing, pp. 247–252, ISBN 978-0-486-67766-8
Dahlquist, Germund; Björck, Åke (2008), "Chapter 5: Numerical Integration", Numerical Methods in Scientific Computing, Volume I, Philadelphia: SIAM, archived from the original on 2007-06-15
Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231
Available in translation as Fourier, Joseph (1878), The analytical theory of heat, Freeman, Alexander (trans.), Cambridge University Press, pp. 200–201
Heath, T. L., ed. (2002), The Works of Archimedes, Dover, ISBN 978-0-486-42084-4
(Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)
Hildebrandt, T. H. (1953), "Integration in abstract spaces", Bulletin of the American Mathematical Society, 59 (2): 111–139, doi:10.1090/S0002-9904-1953-09694-X, ISSN 0273-0979
Kahaner, David; Moler, Cleve; Nash, Stephen (1989), "Chapter 5: Numerical Quadrature", Numerical Methods and Software, Prentice Hall, ISBN 978-0-13-627258-8
Kallio, Bruce Victor (1966), A History of the Definite Integral (PDF) (M.A. thesis), University of British Columbia, archived from the original (PDF) on 2014-03-05, retrieved 2014-02-28
Katz, Victor J. (2004), A History of Mathematics, Brief Version, Addison-Wesley, ISBN 978-0-321-16193-2
Leibniz, Gottfried Wilhelm (1899), Gerhardt, Karl Immanuel (ed.), Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller
Lieb, Elliott; Loss, Michael (2001), Analysis, Graduate Studies in Mathematics, vol. 14 (2nd ed.), American Mathematical Society, ISBN 978-0821827833
Miller, Jeff, Earliest Uses of Symbols of Calculus, retrieved 2009-11-22
O’Connor, J. J.; Robertson, E. F. (1996), A history of the calculus, retrieved 2007-07-09
Rudin, Walter (1987), "Chapter 1: Abstract Integration", Real and Complex Analysis (International ed.), McGraw-Hill, ISBN 978-0-07-100276-9
Saks, Stanisław (1964), Theory of the integral (English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised ed.), New York: Dover
Shea, Marilyn (May 2007), Biography of Zu Chongzhi, University of Maine, retrieved 9 January 2009
Siegmund-Schultze, Reinhard (2008), "Henri Lebesgue", in Timothy Gowers; June Barrow-Green; Imre Leader (eds.), Princeton Companion to Mathematics, Princeton University Press.
Stoer, Josef; Bulirsch, Roland (2002), "Topics in Integration", Introduction to Numerical Analysis (3rd ed.), Springer, ISBN 978-0-387-95452-3.
W3C (2006), Arabic mathematical notation{{citation}}: CS1 maint: numeric names: authors list (link)

External links

"Integral", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Online Integral Calculator, Wolfram Alpha.

Online books

Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
Stroyan, K. D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
Crowell, Benjamin, Calculus, Fullerton College, an online textbook
Garrett, Paul, Notes on First-Year Calculus
Hussain, Faraz, Understanding Calculus, an online textbook
Johnson, William Woolsey (1909) Elementary Treatise on Integral Calculus, link from HathiTrust.
Kowalk, W. P., Integration Theory, University of Oldenburg. A new concept to an old problem. Online textbook
Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
Numerical Methods of Integration at Holistic Numerical Methods Institute
P. S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972) — a cookbook of definite integral techniques

[katz-1] Katz, V.J. 1995. "Ideas of Calculus in Islam and India." Mathematics Magazine (Mathematical Association of America), 68(3):163–174.

[2] In the 20th century, nonstandard analysis was developed as a new approach to calculus that incorporates a rigorous concept of infinitesimals by using an expanded number system called the hyperreal numbers. Though placed on a sound axiomatic footing and of interest in its own right as a new area of investigation, nonstandard analysis remains somewhat controversial from a pedagogical standpoint, with proponents pointing out the intuitive nature of infinitesimals for beginning students of calculus and opponents criticizing the logical complexity of the system as a whole.

[3] (W3C 2006).

[4] Weisstein, Eric W. "Riemann Sum". MathWorld.

[5] Frédéric Chyzak's Mgfun Project: Introduction to the Package Mgfun and Related Packages

[1]

[2]

[3]

[4]

[5]

History

Pre-calculus integration

Newton and Leibniz

Formalization

Historical notation

Applications

Terminology and notation

Standard

Meaning of the symbol dx

Variants

Interpretations of the integral

Formal definitions

Riemann integral

Lebesgue integral

Other integrals

Properties

Linearity

Inequalities

Conventions

Fundamental theorem of calculus

Statements of theorems

Fundamental theorem of calculus

Second fundamental theorem of calculus

Calculating integrals

Extensions

Improper integrals

Multiple integration

Line integrals

Surface integrals

Contour integrals

Integrals of differential forms

Summations

Computation

Analytical

Symbolic

Numerical

Mechanical

Geometrical

See also

References

Bibliography

External links

Online books