Area

Original article: w:Area

This article is about the geometric quantity. For other uses, see Area (disambiguation).

Area
Common symbols	A
SI unit	Square metre [m2]
In SI base units	1 m2

The combined area of these three shapes is approximately 15.57 squares.

넓이(area)는 평면(plane)에서, 이-차원(two-dimensional) 그림 또는 모양(shape), 또는 평면 박판(planar lamina)의 범위를 나타내는 양(quantity)입니다. 표면 넓이(surface area)는 삼-차원 대상(three-dimensional object)의 이-차원 표면(surface) 위의 그것의 아날로그입니다. 넓이는 모양의 모델을 형성하기 위해 필요한 주어진 두께를 가진 재료의 양 또는 단일 외투로 표면을 덮기 위해서 필요한 페인트(paint)의 양으로 이해될 수 있습니다. 그것은 곡선(curve)의 길이(length) (일-차원 개념) 또는 고체의 부피(volume) (삼-차원 개념)의 이-차원 아날로그입니다.

모양의 넓이는 형상을 고정된 크기의 정사각형(square)에 대한 모양과 비교함으로써 측정될 수 있습니다. 단위의 국제 시스템(International System of Units) (SI)에서, 넓이의 표준 단위는 제곱 미터(square metre) (m²으로 쓰임)이며, 이것은 그의 변의 길이는 1 미터(metre)인 정사각형의 넓이입니다. 3 제곱 미터의 넓이를 가진 모양은 세 개의 그러한 정사각형과 같은 넓이를 가집니다. 수학(mathematics)에서, 단위 정사각형(unit square)은 넓이 일을 가지는 것으로 정의되고, 임의의 다른 모양 또는 표면의 넓이는 무-차원(dimensionless) 실수(real number)입니다.

삼각형(triangle), 직사각형(rectangle), 및 원(circle)과 같은 단순한 모양의 넓이에 대한 여러 잘-알려진 공식(formula)이 있습니다. 이러한 공식을 사용하여, 임의의 다각형(polygon)의 넓이는 다각형을 삼각형으로 나눔으로써 구할 수 있습니다. 구부러진 경계를 갖는 모양에 대해, 미적분학(calculus)이 넓이를 계산하기 위해 보통 요구됩니다. 사실, 평면 그림의 넓이를 결정하는 문제는 미적분학의 역사적 발전을 위한 주요한 동기였습니다.

This square and this disk both have the same area (see: squaring the circle).

구(sphere), 원뿔, 또는 원기둥과 같은 고체 모양에 대해, 그의 경계 표면의 넓이는 표면 넓이(surface area)라고 불립니다. 단순한 모양의 표면 넓이에 대한 공식은 고대 그리스인(ancient Greeks)에 의해 계산되었지만, 보다 복잡한 모양의 표면 넓이를 계산하는 것은 보통 다변수 미적분학(multivariable calculus)을 요구합니다.

넓이는 현대 수학에서 중요한 역할을 합니다. 기하학(geometry) 및 미적분학에서 그의 명백한 중요성 외에도, 넓이는 선형 대수(linear algebra)에서 행렬식(determinant)의 정의와 관련이 있고, 미분 기하학(differential geometry)에서 표면의 기본 속성입니다. 해석학(analysis)에서, 평면의 부분-집합의 넓이는, 비록 모든 부분-집합이 측정-가능은 아닐지라도, 르베그 측정(Lebesgue measure)을 사용하여 정의됩니다. 일반적으로, 고등 수학에서 넓이는 이-차원 영역에 대해 부피의 특수한 경우로 보입니다.

넓이는 공리의 사용을 통해 정의될 수 있으며, 그것을 특정 평면의 그림의 모음을 실수의 집합으로의 함수로 정의합니다. 그러한 함수가 존재함을 입증할 수 있습니다.

Formal definition

See also: Jordan measure

"넓이"에 의해 의미되는 것을 정의하기 위한 접근은 공리(axiom)를 통하는 것입니다. "넓이"는 (측정-가능 집합이라고 이름-지은) 특수한 종류의 평면 도형의 모음 M에서 실수 집합으로의 함수로 정의할 수 있으며, 이것은 다음 속성을 만족시킵니다:

• M에서 모든 S에 대해, a(S) ≥ 0.
• 만약 S와 T가 M 안에 있으면, S ∪ T 및 S ∩ T도 그렇고, 역시 a(S∪T) = a(S) + a(T) − a(S∩T)입니다.
• 만약 S ⊆ T와 함께 S와 T가 M 안에 있으면, T − S도 M 안에 있고 a(T−S) = a(T) − a(S)입니다.
• 만약 집합 S가 M 안에 있고 S가 T와 합동이면 T는 역시 M 안에 있고 a(S) = a(T)입니다.
• 모든 각 직사각형 R은 M 안에 있습니다. 만약 직사각형이 길이 h와 폭 k를 가지면, a(R) = hk입니다.
• Q를 두 단계 영역 S와 T 사이에 둘러싸인 집합으로 놓습니다. 단계 영역은 공통 밑변 위에 놓인 인접한 직사각형의 유한 합으로부터 형성됩니다. 즉, S ⊆ Q ⊆ T입니다. 만약 모든 그러한 단계 영역 S와 T에 대해 a(S) ≤ c ≤ a(T)를 만족하는 고유한 숫작 c가 있으면, a(Q) = c입니다.

그러한 넓이 함수가 실제로 존재함을 입증할 수 있습니다.

Units

A square metre quadrat made of PVC pipe.

모든 각 길이의 단위(unit of length)는 대응하는 넓이의 단위, 즉 주어진 변 길이를 갖는 정사각형의 넓이를 가집니다. 따라서 넓이는 제곱 미터 (m²), 제곱 센티미터 (cm²), 제곱 밀리미터 (mm²), 제곱 킬로미터 (km²), 제곱 피터(square feet) (ft²), 제곱 야드 (yd²), 제곱 마일 (mi²), 기타 등등에서 측정될 수 있습니다. 대수적으로, 이들 단위는 대응하는 길이 단위의 제곱(squares)으로 생각될 수 있습니다.

넓이의 SI 단위는 제곱 미터이며, SI 유도 단위(SI derived unit)로 여겨집니다.

Conversions

Although there are 10 mm in 1 cm, there are 100 mm² in 1 cm².

길이와 폭이 1인 정사각형의 넓이의 계산은 다음일 것입니다:

1 metre × 1 metre = 1 m²

따라서, 다른 변을 갖는 직사각형 (말하자면 3미터의 길이와 2미터의 폭)은 다음으로 계산될 수 있는 제곱 단위에서 넓이를 가질 것입니다:

3 미터 × 2 미터 = 6 m². 이것은 6백만 제곱 밀리미터와 동등합니다. 다른 유용한 변환은 다음입니다:

• 1 제곱 킬로미터 = 1,000,000 제곱 미터
• 1 제곱 미터 = 10,000 제곱 센티미터 = 1,000,000 제곱 밀리미터
• 1 제곱 센티미터 = 100 제곱 밀리미터.

Non-metric units

비-메트릭 단위에서, 두 제곱 단위 사이의 변환은 대응하는 길이 단위 사이의 변환의 제곱(square)입니다.

1 피트(foot) = 12 인치(inch),

제곱 피트와 제곱 인치 사이의 관계는 다음입니다:

1 제곱 피트 = 144 제곱 인치,

여기서 144 = 12² = 12 × 12입니다. 비슷하게:

• 1 제곱 야드 = 9 제곱 피트
• 1 제곱 마일 = 3,097,600 제곱 야드 = 27,878,400 제곱 피트

게다가, 변환 인수는 다음을 포함합니다:

• 1 제곱 인치 = 6.4516 제곱 센티미터
• 1 제곱 피트 = 0.09290304 제곱 미터
• 1 제곱 야드 = 0.83612736 제곱 미터
• 1 제곱 마일 = 2.589988110336 제곱 킬로미터

Other units including historical

See also: Category:Units of area

넓이에 대해 여러 다른 공통 단위가 있습니다. 아르(are)는 메트릭 시스템(metric system)에서, 다음과 함께, 넓이의 원래 단위였습니다:

• 1 아르 = 100 제곱 미터

비록 아르가 사용이 중단되었지만, 헥타르(hectare)는 여전히 토지를 측정하기 위해 공통적으로 사용됩니다:

• 1 헥타르 = 100 아르 = 10,000 제곱 미터 = 0.01 제곱 킬로미터

넓이의 다른 비-공통 메트릭 단위는 테트라드(tetrad), 헥타드(hectad), 및 마리아드(myriad)를 포함합니다.

에이커(acre)는 토지 넓이를 측정하기 위해 공통적으로 역시 사용되며, 여기서

• 1 에이커 = 4,840 제곱 야드 = 43,560 제곱 피트.

에이커는 헥타르의 근사적으로 40%입니다.

원자 규모에서, 넓이는 다음을, 만족하는, 바안(barns)의 단위에서 측정됩니다:

• 1 바안 = 10⁻²⁸ 제곱 미터.

바안은 핵 물리학(nuclear physics)에서 교차의 교차-단면 넓이를 설명하는 데 공통적으로 사용됩니다.

인도에서,

• 20 dhurki = 1 dhur
• 20 dhur = 1 khatha
• 20 khata = 1 bigha
• 32 khata = 1 acre

History

Circle area

기원전 5세기에서, 키오스의 히포크라테스(Hippocrates of Chios)는 디스크의 넓이 (원으로 둘러싸인 영역)가 히포크라테스의 달(Lune of Hippocrates)의 구적법(quadrature)의 일부로서, 그것의 지름의 제곱에 비례한다는 것을 처음으로 보였지만, 비례의 상수(constant of proportionality)를 식별하지는 못했습니다. 크니도스의 에우독소스(Eudoxus of Cnidus)는, 역시 기원전 5세기에, 디스크의 넓이가 반지름의 제곱에 비례한다는 것을 발견했습니다.

그 후, 유클리드의 원론(Euclid's Elements)의 책 I은 이-차원 그림 사이의 넓이의 상등 다루었습니다. 수학자 아르키메데스는, 그의 책 Measurement of a Circle에서, 원 내부의 넓이가 그의 밑변이 원의 둘레의 길이를 가지고 그의 높이는 원의 반지름과 같은 직각 삼각형의 넓이와 같음을 보이기 위해 유클리드 기하학의 도구를 사용했습니다. (둘레는 2πr이고, 삼각형의 넓이는 밑변 곱하기 높이의 절반이며, 디스크에 대해 넓이 πr²를 산출합니다.) 아르키메데스는 그의 두-배 방법(his doubling method)과 함께 π (따라서 단위-반지름 원의 넓이)의 값을 근사화했으며, 이것에서 그는 원에 정규 삼각형을 내접시키고 그것의 넓이를 기록하고, 그런-다음 정규 육각형(hexagon)을 만들기 위해 변의 개수를 두 배로 늘리고, 그런-다음 다각형의 널이가 원의 넓이에 가까워지도록 반복적으로 변의 숫자를 두-배로 늘렸습니다 (그리고 외접 다각형(circumscribed polygon)과 같은 작업을 수행했습니다).

1761년에 스위스 과학자 요한 하인리히 램버트(Johann Heinrich Lambert)는 π, 원의 넓이와 제곱 반지름의 비율, 무리수(irrational)임을 입증했으며, 그것은 임의의 두 정수의 몫과 같지 않음을 의미합니다. 1794년에 프랑스의 수학자 아드리앵-마리 르장드르(Adrien-Marie Legendre)는 π²이 무리수임을 입증했습니다; 이것은 역시 π가 무리수임을 입증했습니다. 1882년에, 독일의 수학자 페르디난트 폰 린데만(Ferdinand von Lindemann)은 π가 초월적(transcendental)임을 증명했으며 (유리수 계수를 가진 임의의 다항 방정식(polynomial equation)의 해가 아님), 르장드르(Legendre)와 오일러(Euler) 둘 다에 의해 만들어진 추측을 확인했습니다.

Triangle area

알렉산드리아의 헤론 (또는 히이로)은 그것의 변의 관점에서 삼각형의 넓이에 대해 헤론의 공식(Heron's formula)으로 알려진 것을 발견했었고, 증명은 기원 60년경에 쓰인, 그의 책, Metrica에서 찾아질 수 있습니다. 아르키메데스(Archimedes)는 2세기 전에 공식을 알았었다고 제안해 왔고, Metrica는 고대 세계에서 이용할 수 있는 수학적 지식의 모음이기 때문에, 공식이 해당 연구에서 주어진 참조보다 선행될 가능성이 있습니다.

499년에, 아리아바타(Aryabhata), 인도 수학(Indian mathematics)과 인도 천문학(Indian astronomy)의 고전 시대에서 위대한 수학자(mathematician)-천문학자(astronomer)는 Aryabhatiya에서 밑변 곱하기 높이 절-반으로 삼각형의 넓이를 표현했습니다 (섹션 2.6).

헤론과 동등한 공식은 그리스인과 독립적으로 중국인에 의해 발견되었습니다. 그것은 진규소(Qin Jiushao)에 의해 쓰인 Shushu Jiuzhang ("아홉 부분에서 수학적 논문")에서 1247년에 출판되었습니다.

Quadrilateral area

기원후 7세기에, 브라마굽타(Brahmagupta)는 변의 관점에서 순환 사변형(cyclic quadrilateral) (원에 내접된(inscribed) 사변형(quadrilateral))의 넓이에 대해 현재 브라마굽타의 공식(Brahmagupta's formula)으로 알려진 공식을 개발했습니다. 1842년에 독일의 수학자 카를 안톤 브레치나이더(Carl Anton Bretschneider)와 카를 게오르크 크리스티안 폰 슈타우트(Karl Georg Christian von Staudt)는 독립적으로 임의의 사각형의 넓이에 대한 브레치나이더의 공식(Bretschneider's formula)으로 알려진 공식을 발견했습니다.

General polygon area

17세기에 르네 데카르트(René Descartes)에 의한 데카르트 좌표(Cartesian coordinates)의 개발은 19세기에서 가우스(Gauss)에 의해 알려진 꼭짓점(vertex) 위치를 갖는 임의의 다각형의 넓이에 대해 측량자의 공식(surveyor's formula)의 개발을 가능하게 했습니다.

Areas determined using calculus

17세기 후반에 적분 미적분학(integral calculus)의 개발은 타원(ellipse)의 영역 및 다양한 곡선의 삼-차원 물체의 표면 넓이(surface area)와 같은 보다 복잡한 넓이를 계산하는 데 사용될 수 있는 도구를 제공했습니다.

Area formulas

Polygon formulas

Main article: Polygon § Area and centroid

비-자기-교차하는 (단순(simple)) 다각형. n 꼭짓점(vertices)이 알려져 있는 데카르트 좌표(Cartesian coordinates) $(x_{i},y_{i})$ (i=0, 1, ..., n-1)에 대해, 그 넓이는 측량자의 공식(surveyor's formula)에 의해 제공됩니다:

$A={\frac {1}{2}}|\sum _{i=0}^{n-1}(x_{i}y_{i+1}-x_{i+1}y_{i})|$

여기서 i=n-1일 때, i+1은 모듈러스(modulus) n으로 표현되고 따라서 0으로 참조됩니다.

Rectangles

The area of this rectangle is lw.

가장 기본적인 넓이 공식은 직사각형(rectangle)의 넓이에 대해 공식입니다. 길이 l과 너비 w를 갖는 직사각형이 주어지면, 넓이에 대해 공식은 다음입니다:

A = lw  (직사각형).

즉, 직사각형의 넓이는 길이에 너비를 곱한 것입니다. 특별한 경우로써, 정사각형의 경우에서 l = w이므로, 변 길이 s를 갖는 정사각형의 넓이는 다음 공식에 의해 제공됩니다:

A = s²  (정사각형).

직사각형의 넓이에 대해 공식은 넓이의 기본 속성으로부터 직접 따르고, 때때로 정의(definition) 또는 공리(axiom)로 취급됩니다. 다른 한편으로, 만약 기하학(geometry)이 산술(arithmetic) 전에 개발되었으면, 이 공식은 실수(real number)의 곱셈(multiplication)을 정의하기 위해 사용될 수 있습니다.

Dissection, parallelograms, and triangles

Main articles: Triangle § Computing the area of a triangle, and Parallelogram § Area formula

넓이에 대한 가장 다른 간단한 공식은 절개(dissection)의 방법으로부터 따릅니다. 이것은 모양을 조각으로 자르는 작업을 포함하며, 그것의 넓이는 원래 모양의 넓이와 합(sum)해야 합니다.

A diagram showing how a parallelogram can be re-arranged into the shape of a rectangle.

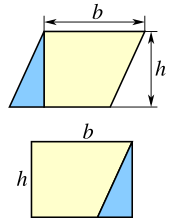
예제에 대해, 임의의 평행-사변형(parallelogram)은, 왼쪽 그림에서 보인 것처럼, 사다리꼴(trapezoid)과 직각 삼각형(right triangle)으로 작게-나누어질 수 있습니다. 만약 그 삼각형이 사다리꼴의 다른 쪽으로 이동되면, 결과 그림은 직사각형입니다. 평행-사변형의 넓이는 직사각형의 넓이와 같음을 따릅니다:

A = bh  (parallelogram).

A parallelogram split into two equal triangles.

어쨌든, 같은 평행사변형은, 오른쪽 그림에서 보인 것처럼, 대각선(diagonal)을 따라 두 개의 합동(congruent) 삼각형으로 역시 자를 수 있습니다. 각 삼각형(triangle)의 넓이는 평행 사변형의 넓이의 절반입니다:

$A={\frac {1}{2}}bh$  (triangle).

비슷한 논증은 사다리꼴(trapezoid)과 마찬가지로 보다 복잡한 다각형(polygon)에 대해 넓이 공식을 찾기 위해 사용될 수 있습니다.

Area of curved shapes

Circles

A circle can be divided into sectors which rearrange to form an approximate parallelogram.

Main article: Area of a circle

원(circle)의 넓이에 대해 공식은 (보다 적절하게 원으로 둘러싸인 넓이 또는 디스크(disk)의 넓이라고 불림) 비스한 방법을 기반으로 합니다. 반지름 r의 원이 주어지면, 오른쪽 그림에서 보이는 것처럼, 원을 부채꼴(sectors)로 분할할 수 있습니다. 각 부채꼴은 근사적으로 모양에서 삼각형이고, 부채꼴은 대략 평행-사변형을 형성하기 위해 재-배열될 수 있습니다. 이 평행-사변형의 높이는 r이고, 너비는 원의 둘레(circumference)의 절반, 또는 πr입니다. 따라서, 원의 전체 넓이는 πr²입니다:

A = πr²  (circle).

비록 이 공식에서 사용된 절개가 단지 근사적일지라도, 오차는 원을 점점 더 많은 부채꼴로 분할할 때 점점 더 작아집니다. 근사적인 평행-사변형의 넓이의 극한(limit)은 정확히 πr²이며, 이것은 원의 넓이입니다.

이 논증은 실제로 미적분학(calculus) 아이디어의 간단한 적용입니다. 고대 시대에서, 소진의 방법(method of exhaustion)이 원의 넓이를 구하기 위해 비슷한 방식으로 사용되었고, 이 방법은 이제 적분 미적분학(integral calculus)의 선구자로 인식됩니다. 현대적인 방법을 사용하여, 원의 넓이는 한정 적분(definite integral)을 사용하여 계산될 수 있습니다:

$A\;=\;2\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx\;=\;\pi r^{2}.$

Ellipses

Main article: Ellipse § Area

타원(ellipse)으로 둘러싸인 넓이의 공식은 원의 공식과 관련이 있습니다; 반-주요(semi-major) 및 반-보조(semi-minor) 축 x와 y를 갖는 타원에 대해, 공식은 다음입니다:

$A=\pi xy.$

Surface area

Main article: Surface area

Archimedes showed that the surface area of a sphere is exactly four times the area of a flat disk of the same radius, and the volume enclosed by the sphere is exactly 2/3 of the volume of a cylinder of the same height and radius.

표면 넓이(surface area)에 대한 대부분의 기본 공식은 표면을 자르고 그들을 평평하게 함으로써 얻어질 수 있습니다. 예를 들어, 원기둥(cylinder) (또는 임의의 각기둥(prism))의 옆 표면이 길이별로 절단되면, 표면은 직사각형으로 평평해질 수 있습니다. 비슷하게, 원뿔(cone)의 옆을 따라 절단이 이루어지면, 옆 표면은 원의 부채꼴로 평평해지고, 결과 넓이는 계산될 수 있습니다.

구의 표면 넓이에 대한 공식은 도출하기가 더 어렵습니다: 구(sphere)는 비-영 가우스 곡률(Gaussian curvature)을 가지기 때문에, 평면화할 수 없습니다. 구의 표면 넓이에 대한 공식은 그의 연구 On the Sphere and Cylinder에서 아르키메데스(Archimedes)에 의해 처음 얻어졌습니다. 공식은 다음입니다:

A = 4πr²  (구), 여기서 r은 구의 반지름입니다. 원의 넓이에 대한 공식과 마찬가지로, 이 공식의 임의의 유도는 기본적으로 미적분(calculus)과 유사한 방법을 사용합니다.

General formulas

Areas of 2-dimensional figures

Triangle area $A={\tfrac {b\cdot h}{2}}$

• 삼각형(triangle): ${\tfrac {1}{2}}Bh$ (여기서 B는 임의의 변이고, h는 B가 놓인 직선에서 삼각형의 다른 꼭짓점까지의 거리입니다). 이 공식은 만약 높이 h가 알려져 있으면 사용될 수 있습니다. 만약 세 변의 길이가 알려져 있으면, 헤론의 공식(Heron's formula)이 사용됩니다: ${\sqrt {s(s-a)(s-b)(s-c)}}$ 여기서 a, b, c는 삼각형의 변이고, $s={\tfrac {1}{2}}(a+b+c)$는 그것의 둘레의 절반입니다. 만약 한 각도와 그것의 두 포함된 변이 주어져 있으면, 넓이는 ${\tfrac {1}{2}}ab\sin(C)$이며 여기서 C는 주어진 각도이고 a와 b는 그것의 포함된 변입니다. 만약 삼각형이 좌표 평면 위에 그려져 있으면, 행렬이 사용될 수 있고 ${\tfrac {1}{2}}(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3})$의 절댓값으로 단순화됩니다. 이 공식은 신발끈 공식(shoelace formula)으로 역시 알려져 있고 세 점 (x₁,y₁), (x₂,y₂), 및 (x₃,y₃)을 대체함으로써 좌표 삼각형의 넓이에 대해 푸는 쉬운 방법입니다. 신발끈 공식은 그들의 꼭짓점이 알려져 있을 때 다른 다각형의 넓이를 찾기 위해 역시 사용될 수 있습니다. 좌표 삼각형에 대해 또 다른 접근은 넓이를 찾기 위해 미적분(calculus)을 사용하는 것입니다.
• 모든 다각형의 꼭짓점이 격자 점인 것을 만족하는 같은-거리 점 (즉, 정수(integer) 좌표를 갖는 점)의 격자 위에 구성된 단순 다각형(simple polygon): $i+{\frac {b}{2}}-1$, 여기서 i는 다각형 안의 격자 점의 숫자이고 b는 경계 점의 숫자입니다. 이 결과는 픽의 정리(Pick's theorem)로 알려져 있습니다.

Area in calculus

Integration can be thought of as measuring the area under a curve, defined by f(x), between two points (here a and b).

The area between two graphs can be evaluated by calculating the difference between the integrals of the two functions

• 수평 축 위에 두 값 a와 b 사이에서 측정된 (b는 두 값 중 더 큰 것으로 정의됨), 양수-값 곡선과 수평 축 사이의 넓이는 곡선에 의해 표현되는 함수의 a에서 b까지의 적분에 의해 주어집니다:

$A=\int _{a}^{b}f(x)\,dx.$

• 두 함수의 그래프(graphs) 사이의 넓이는 하나의 함수(function), f(x)의 적분(integral) 빼기(minus) 또 다른 함수, g(x)의 적분과 같습니다:

$A=\int _{a}^{b}(f(x)-g(x))\,dx,$ 여기서 $f(x)$는 더 큰 y-값을 갖는 곡선입니다.

• 극 좌표(polar coordinates)에서 표현된 함수 r = r(θ)에 의해 경계진 넓이는 다음입니다:

$A={1 \over 2}\int r^{2}\,d\theta .$

• 끝점 ${\vec {u}}(t_{0})={\vec {u}}(t_{1})$을 갖는 매개-변수 곡선(parametric curve) ${\vec {u}}(t)=(x(t),y(t))$에 의해 둘러싸인 넓이는 곡선 적분(line integral)에 의해 주어집니다:

$\oint _{t_{0}}^{t_{1}}x{\dot {y}}\,dt=-\oint _{t_{0}}^{t_{1}}y{\dot {x}}\,dt={1 \over 2}\oint _{t_{0}}^{t_{1}}(x{\dot {y}}-y{\dot {x}})\,dt$

(그린의 정리(Green's theorem)) 또는 다음의 z-성분을 참조하십시오:

${1 \over 2}\oint _{t_{0}}^{t_{1}}{\vec {u}}\times {\dot {\vec {u}}}\,dt.$

Bounded area between two quadratic functions

두 이차 함수(quadratic function) 사이의 경계진 넓이를 찾기 위해, 우리는 다음처럼 차이를 쓰기 위해 하나에서 다른 하나를 뺍니다:

$f(x)-g(x)=ax^{2}+bx+c=a(x-\alpha )(x-\beta )$

여기서 f(x)는 이차 위쪽 경계이고 g(x)는 이차 아래쪽 경계입니다. f(x)-g(x)의 판별식(discriminant)을 다음으로 정의합니다:

$\Delta =b^{2}-4ac.$

두 함수의 그래프 사이의 적분 공식을 단순화하고 (위의 섹션에서 주어진 것처럼) 비에타의 공식(Vieta's formula)을 사용함으로써, 우리는 다음을 획득할 수 있습니다:

$A={\frac {\Delta {\sqrt {\Delta }}}{6a^{2}}}={\frac {a}{6}}(\beta -\alpha )^{3},\qquad a\neq 0.$

위의 것은 만약 경계지는 함수의 하나가 이차 대신에 선형이면 유효하게 남습니다.

Surface area of 3-dimensional figures

• 원뿔(cone): $\pi r\left(r+{\sqrt {r^{2}+h^{2}}}\right)$, 여기서 r은 원형 밑면의 반지름이고, h는 높이입니다. 그것은 $\pi r^{2}+\pi rl$ 또는 $\pi r(r+l)\,\!$으로 역시 다시-쓸 수 있으며 여기서 r은 반지름이고 l은 원뿔의 경사 높이입니다. $\pi r^{2}$은 밑변 넓이이지만, $\pi rl$은 원뿔의 옆쪽 표면 넓이입니다.
• 정육면체(cube): $6s^{2}$, 여기서 s는 가장자리의 길이입니다.
• 원기둥(cylinder): $2\pi r(r+h)$, 여기서 r은 밑변의 반지름이고 h는 높이입니다. 2$\pi$r은 $\pi$ d로 역시 다시-쓸 수 있으며, 여기서 d는 지름입니다.
• 각기둥(prism): 2B + Ph, 여기서 B는 밑면의 넓이이고, P는 밑면의 둘레이고, h는 각기둥의 높이입니다.
• 피라미드(pyramid): $B+{\frac {PL}{2}}$, 여기서 B는 밑면의 넓이이고, P는 밑면의 둘레이고, L은 경사의 길이입니다.
• 직사각형 각기둥(rectangular prism): $2(\ell w+\ell h+wh)$, 여기서 $\ell$는 길이, w는 너비이고, h는 높이입니다.

General formula for surface area

연속적으로 미분-가능 함수 $z=f(x,y)$의 그래프의 표면 넓이에 대해 일반적인 공식은, 여기서 $(x,y)\in D\subset \mathbb {R} ^{2}$ 및 $D$, 매끄러운 경계를 갖는 xy-평면에서 영역입니다:

$A=\iint _{D}{\sqrt {\left({\frac {\partial f}{\partial x}}\right)^{2}+\left({\frac {\partial f}{\partial y}}\right)^{2}+1}}\,dx\,dy.$

벡터 형식 $\mathbf {r} =\mathbf {r} (u,v)$에서 매개변수 표면(parametric surface)의 그래프의 넓이에 대해 훨씬 더 일반적인 공식은, 여기서 $\mathbf {r}$는 $(u,v)\in D\subset \mathbb {R} ^{2}$의 연속적으로 미분-가능 벡터 함수이며, 다음입니다:

$A=\iint _{D}\left|{\frac {\partial \mathbf {r} }{\partial u}}\times {\frac {\partial \mathbf {r} }{\partial v}}\right|\,du\,dv.$

List of formulas

Additional common formulas for area:

Shape	Formula	Variables
정규 삼각형 (등변 삼각형)	${\frac {\sqrt {3}}{4}}s^{2}\,\!$	$s$는 삼각형의 변의 길이입니다.
삼각형	${\sqrt {s(s-a)(s-b)(s-c)}}\,\!$	$s$는 둘레의 절반이며, $a$, $b$ 및 $c$는 각 변의 길이입니다.
삼각형	${\tfrac {1}{2}}ab\sin(C)\,\!$	$a$와 $b$는 두 변이고, $C$는 그들 사이의 각도입니다.
삼각형	${\tfrac {1}{2}}bh\,\!$	$b$와 $h$는, 각각, 밑변(base)과 고도(altitude) (밑변으로부터 수직으로 측정됨)입니다.
이등변 삼각형	${\frac {1}{2}}b{\sqrt {a^{2}-{\frac {b^{2}}{4}}}}={\frac {b}{4}}{\sqrt {4a^{2}-b^{2}}}$	$a$는 두 같은 변 중 하나의 길이이고 $b$는 다른 변의 길이입니다.
마름모/연(Kite)	${\tfrac {1}{2}}ab$	$a$와 $b$는 마름모 또는 연의 두 대각선의 길이입니다.
평행사변형	$bh\,\!$	$b$는 밑변의 길이이고 $h$는 수직 길이입니다.
사다리꼴	${\frac {(a+b)h}{2}}\,\!$	$a$와 $b$는 평행 변의 길이이고 $h$는 두 평행 사이의 거리 (높이)입니다.
정규 육각형	${\frac {3}{2}}{\sqrt {3}}s^{2}\,\!$	$s$는 육각형의 한 변의 길이입니다.
정규 팔각형	$2(1+{\sqrt {2}})s^{2}\,\!$	$s$는 팔각형의 한 변의 길이입니다.
정규 다각형	${\frac {1}{4}}nl^{2}\cdot \cot(\pi /n)\,\!$	$l$은 변 길이이고 $n$은 변의 숫자입니다.
정규 다각형	${\frac {1}{4n}}p^{2}\cdot \cot(\pi /n)\,\!$	$p$는 둘레이고 $n$은 변의 숫자입니다.
정규 다각형	${\frac {1}{2}}nR^{2}\cdot \sin(2\pi /n)=nr^{2}\tan(\pi /n)\,\!$	$R$은 둘레-원의 반지름, $r$은 내접된 원의 반지름이고, $n$은 변의 숫자입니다.
정규 다각형	${\tfrac {1}{2}}ap={\tfrac {1}{2}}nsa\,\!$	$n$은 변의 숫자, $s$는 변의 길이, $a$는 아포팀(apothem), 또는 다각형에서 내접된 원의 반지름이고, $p$는 다각형의 둘레입니다.
원	$\pi r^{2}\ {\text{or}}\ {\frac {\pi d^{2}}{4}}\,\!$	$r$은 반지름이고 $d$는 지름입니다.
원형 부채꼴	${\frac {\theta }{2}}r^{2}\ {\text{or}}\ {\frac {L\cdot r}{2}}\,\!$	$r$과 $\theta$는 각각 반지름과 (라디안에서) 각도이고, $L$은 둘레의 길이입니다.
타원	$\pi ab\,\!$	$a$와 $b$는 각각 반-주요(semi-major)와 반-보조(semi-minor) 축입니다.
원기둥의 전체 표면 넓이	$2\pi r(r+h)\,\!$	$r$과 $h$는, 각각, 반지름과 높이입니다.
원기둥의 옆쪽 표면 넓이	$2\pi rh\,\!$	$r$과 $h$는, 각각, 반지름과 높이입니다.
구의 전체 표면 넓이	$4\pi r^{2}\ {\text{or}}\ \pi d^{2}\,\!$	$r$과 $d$는, 각각, 반지름과 지름입니다.
피라미드의 전체 표면 넓이	$B+{\frac {PL}{2}}\,\!$	$B$는 밑면 넓이, $P$는 밑면 둘레이고 $L$은 경사 높이입니다.
피라미드 절두체의 전체 표면 넓이	$B+{\frac {PL}{2}}\,\!$	$B$는 밑면 넓이, $P$는 밑면 둘레이고 $L$은 경사 높이입니다.
정사각형에서 원형으로 넓이 변환	${\frac {4}{\pi }}A\,\!$	$A$는 정사각형 단위에서 정사각형의 넓이입니다.
원형(Circular)에서 정사각형으로 넓이 변환	${\frac {\pi }{4}}C\,\!$	$C$는 원형 단위에서 원의 넓이입니다.

위의 계산은 많은 공통 모양(shapes)의 넓이를 찾는 방법을 보여줍니다.

비-정규 다각형의 넓이는 "측량자의 공식(Surveyor's formula)"을 사용하여 계산될 수 있습니다..

Relation of area to perimeter

같은-둘레 부등식(isoperimetric inequality)은 길이 L의 닫힌 곡선 (따라서 그것으로 둘러싸는 영역은 둘레(perimeter) L을 가짐)에 대해 및 그것이 둘러싸고 있는 영역의 넓이 A에 대해, 다음임을 말합니다:

$4\pi A\leq L^{2},$

그리고 상등이 유지되는 것과 곡선이 원(circle)인 것은 필요충분 조건입니다. 따라서 원은 주어진 둘레를 갖는 임의의 닫힌 그림의 가장-큰 넓이입니다.

다른 극단적인 것에서, 주어진 둘레 L을 갖는 그림은 마름모(rhombus)의 각도(angle)의 둘이 임의적으로 0°도에 가깝고 다른 둘이 임의적으로 180°에 가깝도록 임의적으로 "뽀족해진" 마름모에 의해 묘사된 것처럼 임의의 작은 넓이를 가질 수 있습니다.

원에 대해, 넓이와 주변(circumference) (원의 둘레에 대해 용어)의 비율은 반지름(radius) r의 절반과 같습니다. 이것은 넓이 공식 πr²과 둘레 공식 2πr으로부터 알 수 있습니다.

정규 다각형(regular polygon)의 넓이는 그것의 둘레 곱하기 아포팀(apothem)의 절반입니다 (여기서 아포팀은 중심으로부터 임의의 변 위의 가장-가까운 점까지의 거리입니다).

Fractals

다각형의 가장자리 길이를 두 배로 늘리면 그것의 넓이에 4가 곱하며, 이것은 2 (다각형이 놓여있는 공간의 차원)의 거듭제곱에 올려진 2 (이전 변 길이에 대한 새로운 것의 비율)입니다. 그러나, 만약 이-차원에서 그려진 프랙탈(fractal)의 일-차원 길이는 모두 두 배되면, 프랙탈의 공간적 컨텐츠는 반드시 정수일 필요는 없는 2의 거듭제곱으로 스케일됩니다. 이 거듭제곱은 프랙탈의 프랙탈 차원(fractal dimension)이라고 불립니다.

Area bisectors

Main article: Bisection § Area bisectors and perimeter bisectors

삼각형의 넓이를 이등분하는 직선의 무한대의 개수가 있습니다. 그들 중의 셋은 삼각형의 중앙선(medians)이고 (변의 중간 점을 반대 꼭짓점과 연결하는 직선), 이들은 삼각형의 도형-중심(centroid)에서 동시에-만납니다; 실제로, 그들은 도형-중심을 통과하는 유일한 넓이 이등분선입니다. 삼각형의 넓이와 둘레 둘 다를 절반으로 나누는 삼각형을 통과하는 직선은 삼각형의 중심 (내원(incircle)의 중심)을 통과합니다. 임의의 주어진 삼각형에 대해 이들의 하나, 둘 또는 셋 중 하나가 있습니다.

평행사변형의 중간점을 통과하는 임의의 직선은 넓이를 이등분합니다.

원 또는 다른 타원의 모든 넓이 이등분선은 중심을 통과하고, 중심을 통과하는 임의의 현(chords)은 넓이를 이등분합니다. 원의 경우에서, 그들은 원의 지름입니다.

Optimization

철사 윤곽이 주어지면, 채우는 가장-작은 넓이의 표면은 최소 표면(minimal surface)입니다. 익숙한 예제는 비누 방울(soap bubble)을 포함합니다.

리만 원(Riemannian circle)의 채우는 넓이(filling area)의 질문은 열린 채 남겨져 있습니다.

원은 같은 둘레를 가지는 임의의 이-차원 물체의 가장-큰 넓이를 가집니다.

순환 다각형(cyclic polygon) (원에 내접하는 다각형)은 같은 길이의 변의 주어진 숫자를 갖는 임의의 다각형의 가장-큰 넓이입니다.

삼각형에 대해 같은-둘레 부등식(isoperimetric inequality)의 버전은 주어진 둘레를 갖는 모든 그들 사이에 가장-큰 넓이의 삼각형은 등변(equilateral)이라고 말합니다.

주어진 원 안에 내접된 모든 삼각형의 가장-큰 넓이의 삼각형은 등변입니다; 그리고 주어진 원 주위로 외접된 삼각형의 가장-작은 넓이의 삼각형은 등변입니다.

내원의 넓이와 등변 삼각형의 넓이의 비율, ${\frac {\pi }{3{\sqrt {3}}}}$은 임의의 비-등변 삼각형의 비율보다 더 큽니다.

정사각형의 넓이와 등변 삼각형의 둘레의 비율, ${\frac {1}{12{\sqrt {3}}}}$은 임의의 다른 삼각형에 대해 그것보다 더 큽니다.

See also

• Brahmagupta quadrilateral, a cyclic quadrilateral with integer sides, integer diagonals, and integer area.
• Equi-areal mapping
• Heronian triangle, a triangle with integer sides and integer area.
• List of triangle inequalities
• One-seventh area triangle, an inner triangle with one-seventh the area of the reference triangle.

• Routh's theorem, a generalization of the one-seventh area triangle.

• Orders of magnitude—A list of areas by size.
• Derivation of the formula of a pentagon
• Planimeter, an instrument for measuring small areas, e.g. on maps.
• Area of a convex quadrilateral
• Region
• Robbins pentagon, a cyclic pentagon whose side lengths and area are all rational numbers.