Vector space

Original article: w:Vector space

Not to be confused with Vector field.

"Linear space" redirects here. For a structure in incidence geometry, see Linear space (geometry).

Vector addition and scalar multiplication: a vector v (blue) is added to another vector w (red, upper illustration). Below, w is stretched by a factor of 2, yielding the sum v + 2w.

수학(mathematics)과 물리학(physics)에서, 벡터 공간(vector space, 역시 선형 공간이라고 불림)은 그것의 원소가, 종종 벡터라고 불리며, 함께 더해질(added) 수 있고 스칼라(scalars)라고 불리는 숫자에 의해 곱해질(multiplied) ("스케일될") 수 있는 집합(set)입니다. 스칼라는 종종 실수로 취해지지만, 복소수, 또는, 더 일반적으로, 임의의 필드(field)의 원소가 될 수 있습니다. 벡터 덧셈과 스칼라 곱셈의 연산은 벡터 공리(axiom)라고 불리는 특정 요구 사항을 만족시켜야 합니다. 용어 실수 벡터 공간(real vector space)과 복소 벡터 공간(complex vector space)은 종종 스칼라의 본성: 실수 좌표 공간 또는 복소 좌표 공간을 지정하기 위해 자주 사용됩니다.

벡터 공간은 크기 뿐만 아니라 방향도 가지는 힘(forces)과 속도(velocity)와 같은 물리적 양(physical quantities)의 모델링을 허용하는 유클리드 벡터(Euclidean vectors)를 일반화합니다. 벡터 공간의 개념은 벡터 공간에서 계산을 허용하는 행렬(matrix)의 개념과 함께 선형 대수(linear algebra)의 기본입니다. 이것은 선형 방정식의 시스템(systems of linear equations)을 조작하고 연구하기 위한 간결하고 종합적인 방법을 제공합니다.

벡터 공간은 대략적으로 말하면 공간에서 독립적인 방향의 수를 지정하는 그것들의 차원(dimension)에 의해 특징지어집니다. 이것은, 동일한 차원을 갖는 두 벡터 공간에 대해, 벡터 공간 구조에만 의존하는 속성이 정확히 같다는 것을 의미합니다 (기술적으로 벡터 공간은 동형적(isomorphic)입니다). 벡터 공간은 만약 그것의 차원이 자연수이면 유한-차원(finite-dimensional)입니다. 그렇지 않으면, 그것은 무한-차원(infinite-dimensional)이고, 그것의 차원은 무한 세는-숫자(infinite cardinal)입니다. 유한-차원 벡터 공간은 기하학(geometry)과 관련된 영역에서 자연스럽게 발생합니다. 무한-차원 벡터 공간은 수학의 많은 영역에서 발생합니다. 예를 들어, 다항식 링(polynomial rings)은 셀-수-있는 무한-차원 벡터 공간이고, 많은 함수 공간(function spaces)은 연속체의 카디널리티(cardinality of the continuum)를 차원으로 가지고 있습니다.

수학에서 고려되는 많은 벡터 공간은 다른 구조도 부여됩니다. 이것은 필드 확장(field extensions), 다항식 링(polynomial rings), 결합 대수(associative algebras), 및 리 대수(Lie algebras)를 포함하는 대수의 경우입니다. 이것은 함수 공간(function spaces), 안의 곱 공간(inner product spaces), 노름 공간(normed spaces), 힐베르트 공간(Hilbert spaces), 및 바나흐 공간(Banach spaces)을 포함하는 토폴로지적 벡터 공간의 경우이기도 합니다.

Definition and basic properties

이 기사에서, 벡터는 스칼라와 구별하기 위해 굵게 표시됩니다.

필드(field) F에 걸쳐 벡터 공간은 아래 나열된 8가지 공리를 만족시키는 두 개의 이항 연산(binary operations)과 함께 집합(set) V입니다. 이러한 맥락에서, V의 원소는 공통적으로 벡터(vectors)라고 불리고, F의 원소는 스칼라(scalars)라고 불립니다.

• 벡터 덧셈 또는 단순히 덧셈이라고 하는 첫 번째 연산은 V에서 임의의 두 벡터 v와 w에 V에서 세 번째 벡터를 할당하며, 이는 공통적으로 v + w로 쓰이고, 이들 두 벡터의 합이라고 불립니다.
• 스칼라 곱셈(scalar multiplication)이라고 하는 두 번째 연산은 F에서 임의의 스칼라 a와 V에서 임의의 벡터 v에 av로 표시되는 V에서 또 다른 벡터를 할당합니다.

벡터 공간을 가지는 것에 대해, V에서 모든 각 u, v 및 w, F에서 a와 b에 대해 다음 8가지 공리(axioms)가 만족되어야 합니다.

Axiom	Meaning
벡터 덧셈의 결합성(Associativity)	u + (v + w) = (u + v) + w
벡터 덧셈의 교환성(Commutativity)	u + v = v + u
벡터 덧셈의 항등 원소(Identity element)	모든 v ∈ V에 대해 v + 0 = v를 만족하는, 영 벡터(zero vector)라고 불리는 원소 0 ∈ V가 존재합니다.
벡터 덧셈의 역 원소(Inverse elements)	모든 각 v ∈ V에 대해, v + (−v) = 0를 만족하는, v의 덧셈 역원(additive inverse)이라고 불리는, 원소 −v ∈ V가 존재합니다.
스칼라 곱셈과 필드 곱셈의 호환성	a(bv) = (ab)v
스칼라 곱셈의 항등 원소	1v = v, 여기서 1은 F에서 곱셈의 항등원(multiplicative identity)을 나타냅니다.
벡터 덧셈에 관한 스칼라 곱셈의 분배성(Distributivity)	a(u + v) = au + av
필드 덧셈에 관한 스칼라 곱셈의 분배성	(a + b)v = av + bv

스칼라 필드가 실수일 때, 그 벡터 공간은 실수 벡터 공간이라고 불립니다. 스칼라 필드가 복소수일 때, 그 벡터 공간은 복소수 벡터 공간이라고 불립니다. 이들 두 경우가 가장 공통적인 경우이지만, 임의적인 필드 F에서 스칼라를 갖는 벡터 공간도 공통적으로 고려됩니다. 그러한 벡터 공간은 F-벡터 공간 또는 F에 걸쳐 벡터 공간이라고 불립니다.

훨씬 더 간결하지만 덜 기본적인 벡터 공간의 동등한 정의가 주어질 수 있습니다: 처음 4개의 공리는 벡터 공간이 덧셈 아래의 아벨 그룹(abelian group)이라고 말하고, 4개의 남아있는 공리는 스칼라 곱셈이 필드 F에서 이 그룹의 자기-사상 링(endomorphism ring)으로 링 준동형(ring homomorphism)을 정의한다고 말합니다.

두 벡터의 뺄셈은 다음으로 정의될 수 있습니다:

$\mathbf {v} -\mathbf {w} =\mathbf {v} +(-\mathbf {w} ).$

공리의 직접 결과는 모든 각 $s\in F$와 $\mathbf {v} \in V$에 대해, 다음을 가짐을 포함합니다:

• $0\mathbf {v} =\mathbf {0} ,$
• $s\mathbf {0} =\mathbf {0} ,$
• $(-1)\mathbf {v} =-\mathbf {v} ,$
• $s\mathbf {v} =\mathbf {0}$는 $s=0$ 또는 $\mathbf {v} =\mathbf {0}$을 의미합니다.

Related concepts and properties

A vector v in R² (blue) expressed in terms of different bases: using the standard basis of R²: v = xe₁ + ye₂ (black), and using a different, non-orthogonal basis: v = f₁ + f₂ (red).

선형 조합(Linear combination)

F-벡터 공간 V의 원소의 집합 G가 주어지면, G의 원소의 선형 조합은 다음 형식의 V의 원소입니다: $$a_{1}\mathbf {g} _{1}+a_{2}\mathbf {g} _{2}+\cdots +a_{k}\mathbf {g} _{k},$$여기서 $a_{1},\ldots ,a_{k}\in F$와 $\mathbf {g} _{1},\ldots ,\mathbf {g} _{k}\in G$입니다. 스칼라 $a_{1},\ldots ,a_{k}$는 선형 조합의 계수(coefficients)라고 불립니다.

선형 독립(Linear independence)

F-벡터 공간 V의 부분집합 G의 원소는 G의 원소가 G의 다른 원소의 선형 조합으로 쓰일 수 없으면 선형적으로 독립이라고 말합니다. 동등하게, 그것들은 G의 원소의 두 선형 조합이 같은 V의 원소를 정의하면 선형적으로 독립인 것과 그것들이 같은 계수를 가지는 것은 필요충분 조건입니다. 역시 동등하게, 그것들이 선형 조합이 영 벡터를 초래하면 선형적으로 독립인 것과 모든 계수가 영인 것은 필요충분 조건입니다.

선형 부분공간(Linear subspace)

벡터 공간 V의 선형 부분공간 또는 벡터 부분공간 W는 벡터 덧셈과 스칼라 곱셈 아래에서 닫힌 V의 비-빈 부분집합입니다; 즉, W의 두 원소의 합과 V의 원소에 스칼라를 곱한 값은 W에 속합니다. 이것은 W의 원소의 모든 각 선형 조합이 W에 속한다는 것을 의미합니다. 선형 부분-공간은 유도된 덧셈과 스칼라 곱셈에 대해 벡터 공간입니다; 이것은 클로저 속성이 벡터 공간의 공리가 만족시킴을 암시함을 의미합니다.

클로저 속성은 역시 선형 부분-공간의 모든 각 교집합(intersection)이 선형 부분-공간임을 의미합니다.

선형 스팬(Linear span)

벡터 공간 V의 부분-집합 G가 주어지면, G의 선형 스팬 또는 단순히 스팬은 G를 포함하는 모든 선형 부분-공간의 교차점이라는 의미에서, G를 포함하는 V의 가장 작은 선형 부분-공간입니다. G의 스팬 역시 G의 원소의 모든 선형 조합의 집합입니다. 만약 W가 G의 스팬이면, G는 W를 스팬하거나 W를 생성하고, G는 W의 스팬하는 집합 또는 생성하는 집합이라고 말합니다.

기저(Basis)와 차원(dimension)

벡터 공간의 부분-집합은 그 원소가 선형적으로 독립이고 벡터 공간을 스팬하면 기저입니다. 모든 각 벡터 공간은 적어도 하나의 기저를 가지며, 일반적으로 많이 가집니다 (Basis (linear algebra) § Proof that every vector space has a basis를 참조하십시오). 더욱이, 벡터 공간의 모든 기저는 벡터 공간의 차원이라고 불리는 같은 카디널리티(cardinality)를 가집니다 (벡터 공간에 대해 차원 정리를 참조하십시오). 이것은 벡터 공간의 기본 속성이며, 이는 섹션의 나머지 부분에서 자세히 설명됩니다.

기저는 특히 차원이 유한할 때 벡터 공간 연구를 위한 기본 도구입니다. 무한-차원의 경우에서, 종종 하멜 기저(Hamel bases)라고 불리는 무한 기저의 존재는 선택의 공리(axiom of choice)에 의존합니다. 일반적으로, 기저는 명시적으로 설명될 수 없음을 따릅니다. 예를 들어, 실수는 유리수에 걸쳐 무한-차원 벡터 공간을 형성하며, 이에 대한 구체적인 기저는 알려져 있지 않습니다.

필드 F에 걸쳐 차원 n의 벡터 공간 V의 기저 $(\mathbf {b} _{1},\mathbf {b} _{2},\ldots ,\mathbf {b} _{n})$를 생각해 보십시오. 기저의 정의는 모든 각 $\mathbf {v} \in V$가 F에서 $a_{1},\dots ,a_{n}$를 갖는 다음으로 쓰일 수 있고, 이 분해가 고유함을 의미합니다:

$\mathbf {v} =a_{1}\mathbf {b} _{1}+\cdots +a_{n}\mathbf {b} _{n},$

스칼라 $a_{1},\ldots ,a_{n}$은 기저 위에 v의 좌표라고 불립니다. 그것들은 역시 기저 위에 v의 분해의 계수라고 말합니다. F의 원소의 n-튜플의 집합 $F^{n}$은 차원이 n인 성분-별(componentwise) 덧셈과 스칼라 곱셈에 대해 벡터 공간이기 때문에, 역시 계수의 n-튜플이 기저 위의 v의 좌표 벡터라고 말합니다.

벡터와 그것들의 좌표 벡터 사이의 일-대-일 대응(one-to-one correspondence)은 벡터 덧셈을 벡터 덧셈으로 매핑하고 스칼라 곱셈을 스칼라 곱셈으로 매핑합니다. 그것은 따라서 벡터 공간 동형이며, 이는 벡터 위에 추론과 계산을 그것들의 좌표 위에 추론과 계산으로 변환하는 것을 허용합니다. 만약, 차례로, 이들 좌표가 행렬로 배열되면, 좌표 위에 이들 추론과 계산은 행렬 위에 추론과 계산으로 간결하게 표현될 수 있습니다. 더욱이, 행렬과 관련된 선형 방정식은 선형 방정식의 시스템으로 확장될 수 있고, 역으로, 모든 각 그러한 시스템은 행렬 위에 선형 방정식으로 압축될 수 있습니다.

따라서, 요약하자면, 유한-차원 선형 대수(linear algebra)는 다음 세 가지 동등한 언어로 표현될 수 있습니다:

• 벡터 공간(Vector spaces), 이는 간결하고 좌표-없는 명제를 제공합니다.
• 행렬(Matrices), 이는 간결하게 명시적 계산을 표현하는 데 편리합니다.
• 선형 방정식의 시스템(Systems of linear equations), 이는 더 기본적인 형식화를 제공합니다.

History

벡터 공간은 평면 또는 삼-차원 공간에서 좌표(coordinates)의 도입을 통해 아핀 기하학(affine geometry)에서 유래합니다. 1636년경, 프랑스 수학자 르네 데카르트(René Descartes)와 피에르 드 페르마(Pierre de Fermat)는 평면 곡선(curve) 위의 점을 갖는 두 변수의 방정식에 대한 해를 식별함으로써 해석적 기하학(analytic geometry)을 설립했습니다. 좌표를 사용하는 것 없이 기하학적 해를 달성하기 위해, 볼차노(Bolzano)는 1804년에 벡터의 전신인 점, 직선, 및 평면에 대한 특정 연산을 도입했습니다. Möbius (1827)는 베리-센터 좌표(barycentric coordinates)의 개념을 도입했습니다. Bellavitis (1833)는 쌍-점(bipoint), 즉, 한쪽 끝이 원점이고 다른 쪽 끝이 목표인 방향화된 선분의 개념을 도입했습니다. 벡터는 아르강(Argand)과 해밀턴(Hamilton)에 의해 복소수의 표시와 해밀턴에 의해 쿼터니언(quaternions)의 시작과 함께 재검토되었습니다. 그것들은 R²와 R⁴에서 원소입니다; 그것들을 선형 조합을 사용하여 처리하는 것은 1867년 라게르(Laguerre)로 거슬러 올라가며, 그는 선형 방정식의 시스템(systems of linear equations)도 정의했습니다.

1857년, 케일리(Cayley)는 선형 맵(linear maps)의 조화와 단순화를 허용하는 행렬 표기법(matrix notation)을 도입했습니다. 같은 시기에, 그라스만(Grassmann)은 뫼비우스에 의해 시작된 베리-센터 계산을 연구했습니다. 그는 연산을 갖춘 추상적인 대상의 집합을 구상했습니다. 그의 연구에서, 선형 독립성(linear independence)과 차원(dimension)의 개념과 스칼라 곱(scalar products)이 있습니다. 실제로 그라스만(Grassmann)의 1844년 연구는 벡터 공간의 프레임을 뛰어넘었는데, 왜냐하면 그의 고려하는 곱셈은, 역시, 오늘날 대수(algebras)라고 불리는 것으로 그를 이끌었기 때문입니다. 이탈리아 수학자 페아노(Peano)는 1888년에 벡터 공간과 선형 맵의 현대적인 정의를 최초로 제시했습니다.

벡터 공간의 중요한 발전은 앙리 르베그(Henri Lebesgue)에 의해 함수 공간(function spaces)의 구성에 기인합니다. 이것은 나중에 1920년경 바나흐(Banach)와 힐베르트(Hilbert)에 의해 형식화되었습니다. 그 당시에, 대수와 새로운 함수형 해석학(functional analysis)의 분야가 상호 작용하기 시작했으며, 특히 p-적분가능 함수의 공간과 힐베르트 공간과 같은 주요 개념과 상호 작용하기 시작했습니다. 역시 이 당시에, 무한-차원 벡터 공간에 관한 최초의 연구가 이루어졌습니다.

Examples

Main article: Examples of vector spaces

Arrows in the plane

벡터 공간의 첫 번째 예제는 하나의 고정된 점에서 시작하는 고정된 평면(plane)의 화살표(arrows)로 구성됩니다. 이것은 물리학에서 힘(forces) 또는 속도(velocities)를 설명하기 위해 사용됩니다. 임의의 두 개의 그러한 화살표, v와 w가 주어지면, 이들 두 화살표에 의해 확장되는 평행사변형(parallelogram)도 원점에서 시작하는 하나의 대각선 화살표를 포함합니다. 이러한 새로운 화살표는 두 화살표의 합이라고 불리고, v + w로 표시됩니다. 같은 직선 위에 두 개의 화살표가 있는 특별한 경우에서, 그것들의 합은 화살표가 같은 방향을 가지고 있는지 여부에 따라 길이가 합 또는 길이의 차이인 이 직선의 화살표입니다. 화살표로 수행될 수 있는 또 다른 연산은 스케일링입니다: 임의의 양의 실수 a가 주어지면, v와 방향이 같지만 길이에 a를 곱함으로써 확장되거나 축소되는 화살표는 v와 a의 곱셈이라고 불립니다. 그것은 av로 표시됩니다. a가 음수일 때, av는 반대 방향을 가리키는 화살표로 대신 정의됩니다.

다음은 몇 가지 예제를 보여줍니다: 만약 a = 2이면, 결과 벡터 aw는 w와 같은 방향을 가지지만, w의 두 배 길이로 늘어납니다 (아래 오른쪽 이미지). 동등하게, 2w는 w + w의 합입니다. 게다가, (−1)v = −v는 v와 반대 방향을 가지고 같은 길이를 가집니다 (오른쪽 이미지에서 아래쪽을 가리키는 파란색 벡터입니다).

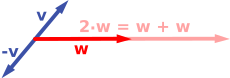
Second example: ordered pairs of numbers

벡터 공간의 두 번째 핵심 예제는 실수 x와 y의 쌍에 의해 제공됩니다. (성분 x와 y의 순서는 중요하므로, 그러한 쌍은 순서화된 쌍(ordered pair)이라고도 불립니다.) 그러한 쌍은 (x, y)로 쓰입니다. 두 개의 그러한 쌍의 합과 한 쌍을 숫자와 곱셈은 다음과 같이 정의됩니다:

$(x_{1},y_{1})+(x_{2},y_{2})=(x_{1}+x_{2},y_{1}+y_{2})$

그리고

$a(x,y)=(ax,ay).$

위의 첫 번째 예제는 만약 화살표가 그 끝점의 데카르트 좌표(Cartesian coordinates)의 쌍에 의해 표시되면 이 예제로 축소됩니다.

Coordinate space

필드 F에 걸쳐 벡터 공간의 가장 간단한 예제는 그것의 덧셈 (벡터 덧셈이 됨) 및 곱셈 (스칼라 곱셈이 됨)을 갖춘 필드 F 자체입니다 (그것이 덧셈에 대해 아벨 그룹이므로, 필드가 되기 위한 요구 사항의 일부입니다). 보다 일반적으로, F의 원소 a_i의 모든 n-튜플 (길이 n의 수열)은

(a₁, a₂, ..., a_n)

보통 Fⁿ으로 표시되고 좌표 공간이라고 불리는 벡터 공간(coordinate space)을 형성합니다. 경우 n = 1은 위에서 언급된 가장 단순한 예제이며, 이것에서 필드 F는 역시 자체에 결처 벡터 공간으로 여겨집니다. 경우 F = R과 n = 2 (따라서 R²)는 위의 도입 부분에서 논의되었습니다.

Complex numbers and other field extensions

복소수의 집합 C, 즉, 실수 x와 y에 대해 x + iy 형식으로 쓸 수 있는 숫자는, 여기서 i는 허수 단위(imaginary unit)이며, 보통의 덧셈과 곱셈을 갖는 실수에 걸쳐 벡터 공간을 형성합니다: 실수 x, y, a, b, 및 c에 대해, (x + iy) + (a + ib) = (x + a) + i(y + b)와 c ⋅ (x + iy) = (c ⋅ x) + i(c ⋅ y). 벡터 공간의 다양한 공리는 복소수 산술에 대해 같은 규칙이 적용된다는 사실에서 비롯됩니다.

사실, 복소수의 예는 위에서 언급된 실수의 순서화된 쌍의 벡터 공간과 본질적으로 같습니다 (즉, 그것은 벡터 공간에 동형적입니다): 복소수 x + i y를 복소 평면(complex plane)에서 순서화된 쌍 (x, y)으로 생각하면 덧셈과 스칼라 곱셈에 대해 규칙이 이전 예의 규칙과 정확히 일치함을 알 수 있습니다.

보다 일반적으로, 필드 확장(field extensions)은 특히 대수와 대수적 숫자 이론에서 벡터 공간의 또 다른 클래스의 예제를 제공합니다: 더 작은 필드 E를 포함하는 필드 F는 F의 주어진 곱셈과 덧셈 연산에 의해 E-벡터 공간입니다. 예를 들어, 복소수는 R에 걸쳐 벡터 공간이고, 필드 확장 $\mathbf {Q} (i{\sqrt {5}})$는 Q에 걸쳐 벡터 공간입니다.

Function spaces

Main article: Function space

Addition of functions: The sum of the sine and the exponential function is $\sin +\exp :\mathbb {R} \to \mathbb {R}$ with $(\sin +\exp )(x)=\sin(x)+\exp(x)$

임의의 고정된 집합 Ω에서 필드 F로의 함수도 점-별 덧셈과 스칼라 곱셈을 수행함으로써 벡터 공간을 형성합니다. 즉, 두 함수 f와 g의 합은 다음과 같이 주어진 함수 (f + g)입니다:

(f + g)(w) = f(w) + g(w),

그리고 곱셈에 대한 것도 유사합니다. 그러한 함수 공간은 Ω가 실수 직선(real line) 또는 구간(interval), 또는 R의 다른 부분-집합(subsets)일 때 많은 기하학적 상황에서 발생합니다. 연속성(continuity), 적분가능성(integrability) 또는 미분가능성(differentiability)과 같은 토폴로지와 해석학의 많은 개념은 선형성과 관련하여 잘-작동합니다: 그러한 속성을 소유한 함수의 합과 스칼라 배수는 여전히 그 속성을 가지고 있습니다. 그러므로, 그러한 함수의 집합은 함수형 해석학(functional analysis)에 속하는 벡터 공간입니다.

Linear equations

Main articles: Linear equation, Linear differential equation, and Systems of linear equations

동차 선형 방정식(homogeneous linear equations)의 시스템은 벡터 공간과 밀접하게 연결되어 있습니다. 예를 들어, 다음의 해는

${\begin{aligned}a+3b+c&=0\\4a+2b+2c&=0\end{aligned}}$

임의적인 a, b = a/2, 및 c = −5a/2를 갖는 세-쌍에 의해 주어집니다. 그것들은 벡터 공간을 형성합니다: 그러한 세-쌍의 합과 스칼라 배수는 여전히 세 변수의 같은 비율을 만족시킵니다; 따라서 그것들도 해입니다. 행렬(Matrices)은 위와 같이 여러 선형 방정식을 하나의 벡터 방정식으로 압축하는 데 사용할 수 있으며, 즉,

Ax = 0,

여기서 $A={\begin{bmatrix}1&3&1\\4&2&2\end{bmatrix}}$는 주어진 방정식의 계수를 포함하는 행렬이고, x는 벡터 (a, b, c)이고, Ax는 행렬 곱(matrix product)을 나타내고, 0 = (0, 0)은 영 벡터입니다. 비슷한 맥락에서, 동차 선형 미분 방정식의 해는 벡터 공간을 형성합니다. 예를 들어, 다음은

f′′(x) + 2f′(x) + f(x) = 0

f(x) = a e^−x + bx e^−x를 산출하며, 여기서 a와 b는 임의적인 상수이고, e^x는 자연 지수 함수(natural exponential function)입니다.

Linear maps and matrices

Main article: Linear map

두 벡터 공간의 관계는 선형 맵 또는 선형 변환으로 표현될 수 있습니다. 그것들은 벡터 공간 구조를 반영하는 함수(functions)입니다. 즉, 그것들은 합과 스칼라 곱셈을 보존합니다:

V에서 모든 v와 w, F에서 모든 a에 대해, $f(\mathbf {v} +\mathbf {w} )=f(\mathbf {v} )+f(\mathbf {w} )$이고 f(a · v) = a · f(v)입니다.

동형(isomorphism)은 두 가능한 합성(compositions) f ∘ g : W → W와 g ∘ f : V → V가 항등 맵(identity maps)을 만족하는 맵인 역 맵(inverse map) g : W → V가 존재함을 만족하는 선형 맵 f : V → W입니다. 동등하게, f는 일-대-일 (단사)와 위로의 (전사) 둘 다입니다. 만약 V와 W 사이에 동형이 존재하면, 두 공간은 동형적이라고 말합니다; 그것들은 V에서 보유하는 모든 항등이, f를 통해, W에서 유사한 항등으로 전송되고 그 반대도 g를 통해 전송되기 때문에 벡터 공간과 본질적으로 동일합니다.

Describing an arrow vector v by its coordinates x and y yields an isomorphism of vector spaces.

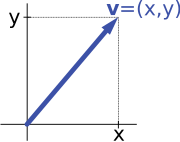
예를 들어, 도입부에서 "평면에서 화살표" 및 "숫자의 순서화된 쌍" 벡터 공간은 동형적입니다: 일부 (고정된) 좌표 시스템(coordinate system)의 원점(origin)에서 출발하는 평면 화살표 v는 오른쪽 이미지와 같이 화살표의 x- 및 y-성분을 고려함으로써 순서화된 쌍으로 표현될 수 있습니다. 반대로, 쌍 (x, y)이 주어지면, x만큼 오른쪽 (또는 x가 음수이면 왼쪽)으로 이동하고 y만큼 위쪽 (y가 음수이면 아래쪽)으로 가는 화살표는 화살표 v를 되돌립니다.

두 벡터 공간 사이의 선형 맵 V → W은 L(V, W), 또는 𝓛(V, W)라고 표시되는 벡터 공간 Hom_F(V, W)를 형성합니다. V에서 F로의 선형 맵의 공간은 $V^{*}$으로 표시된 이중 벡터 공간(dual vector space)이라고 불립니다. 단사 자연(natural) 맵 $V\to V^{**}$을 통해, 임의의 벡터 공간은 그것의 쌍-이중(bidual)에 삽입될 수 있습니다; 그 맵이 동형인 것과 그 공간이 유한-차원인 것은 필요충분 조건입니다.

일단 V의 기저가 선택되면, V의 임의의 원소가 그것들의 선형 조합으로 고유하게 표현되기 때문에, 선형 맵 f : V → W은 기저 벡터의 이미지를 지정함으로써 완전하게 결정됩니다. 만약 dim V = dim W이면, V와 W의 고정된 기저 사이의 1-대-1 대응은 V의 임의의 기저 원소를 W의 대응하는 기저 원소에 매핑하는 선형 맵을 생성합니다. 그것은 바로 정의에 의해 동형입니다. 그러므로, 두 벡터 공간은 만약 그것들의 차원이 일치하고 동형적이고 그 반대도 마찬가지입니다. 이것을 표현하는 또 다른 방법은 임의의 벡터 공간이 그것의 차원, 단일 숫자에 의해 (동형까지(up to)) 완전하게 분류된다는 것입니다. 특히, 임의의 n-차원 F-벡터 공간 V는 Fⁿ과 동형적입니다. 어쨌든, "정식" 또는 선호되는 동형은 없습니다; 실제로 동형 φ : Fⁿ → V는 φ를 통해 Fⁿ의 표준 기저를 V에 매핑함으로써 V의 기저의 선택과 동등합니다. 편리한 기저를 선택하는 것의 자유는 무한-차원 문맥에서 특히 유용합니다; 아래를 참조하십시오.

Matrices

Main articles: Matrix and Determinant

A typical matrix

행렬은 선형 맵을 인코딩하기 위한 유용한 개념입니다. 그것들은 오른쪽 이미지에서 처럼 스칼라의 직사각형 배열로 쓰입니다. 임의의 mxn 행렬 A는 다음과 같이 Fⁿ에서 F^m으로의 선형 맵을 야기합니다:

$\mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})\mapsto \left(\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\ldots ,\sum _{j=1}^{n}a_{mj}x_{j}\right)$, 여기서 $\sum$는 합계(summation)를 나타냅니다,

또는, 좌표 벡터 x와 행렬 A의 행렬 곱셈(matrix multiplication)을 사용하여:

x ↦ Ax.

더욱이, V와 W의 지저를 선택한 후, 임의의 선형 맵 f : V → W는 이 할당을 통해 행렬에 의해 고유하게 표현됩니다.

The volume of this parallelepiped is the absolute value of the determinant of the 3-by-3 matrix formed by the vectors r₁, r₂, and r₃.

정사각 행렬 A의 행렬식(determinant) det (A)는 결합된 맵이 동형인지 여부를 알려주는 스칼라입니다: 따라서 행렬식이 비-영인 것으로 충분이고 필요입니다. 실수 nxn 행렬에 해당하는 Rⁿ의 선형 변환이 방향 보존하는(orientation preserving) 것과 그것의 행렬식이 양수인 것은 필요충분 조건입니다.

Eigenvalues and eigenvectors

Main article: Eigenvalues and eigenvectors

자기-사상(endomorphism), 선형 맵 f : V → V는, 이 경우에서 벡터 v가 f 아래에서 그것의 이미지, f(v)와 비교될 수 있기 때문에 특히 중요합니다. λv = f(v)를 만족시키는 임의의 비-영 벡터 v는, 여기서 λ는 스칼라이며, 고윳값 λ를 갖는 f의 고유벡터라고 불립니다. 동등하게, v는 차이 f − λ · Id의 커널의 원소입니다 (여기서 Id는 항등 맵 V → V입니다). 만약 V가 유한-차원이면, 이것은 행렬식을 사용하여 다시 표현될 수 있습니다: 고윳값 λ를 가지는 f는 다음과 동등합니다:

det(f − λ · Id) = 0.

행렬식의 정의를 설명함으로써, 왼쪽 편에 있는 표현은 f의 특성 다항식(characteristic polynomial)이라고 불리는 λ에서 다항 함수로 볼 수 있습니다. 만약 필드 F가 이 다항식의 영을 포함할 만큼 충분히 크면 (F = C와 같이 대수적으로 닫힌 F에 대해 자동으로 발생), 임의의 선형 맵은 적어도 하나의 고유벡터를 가집니다. 벡터 공간 V는 고유-벡터로 구성된 기저, 고유-기저(eigenbasis)를 보유할 수도 있고 보유하지 않을 수도 있습니다. 이 현상은 맵의 조르당 정식 형식(Jordan canonical form)에 의해 결정됩니다. f의 특정 고윳값에 해당하는 모든 고유벡터의 집합은 질문에서 고윳값 (및 f)에 해당하는 고유-공간(eigenspace)으로 알려진 벡터 공간을 형성합니다. 스펙트럼 정리, 무한-차원의 경우에 해당하는 명제를 달성하기 위해, 함수형 해석학의 기계가 필요됩니다 (아래 참조).

Basic constructions

위의 구체적인 예 외에도, 주어진 것과 관련된 벡터 공간을 산출하는 표준 선형 대수적 구조가 많이 있습니다. 아래에 제공된 정의 외에도, 그것들은 역시 X에서 임의의 다른 벡터 공간으로의 선형 맵을 지정함으로써 대상 X를 결정하는 보편적 속성(universal properties)에 의해 특징짓습니다.

Subspaces and quotient spaces

Main articles: Linear subspace and Quotient vector space

A line passing through the origin (blue, thick) in R³ is a linear subspace. It is the intersection of two planes (green and yellow).

덧셈과 스칼라 곱셈 아래에서 닫혀 있는 (및 따라서 V의 0-벡터를 포함하는) 벡터 공간 V의 비-빈 부분집합(subset) W는 주변 공간이 모호하지 않게 벡터 공간일 때 V의 선형 부분공간 또는 단순히 V의 부분공간이라고 불립니다. V의 부분공간은 그 자체로 (같은 필드에 걸쳐) 벡터 공간입니다. 주어진 벡터의 집합 S를 포함하는 모든 부분공간의 교집합은 그것의 스팬(span)이라고 불리고, 그것은 집합 S를 포함하는 V의 가장 작은 부분공간입니다. 원소의 관점에서 표현된, 스팬은 S의 원소의 모든 선형 조합(linear combinations)으로 구성된 부분공간입니다.

차원 1의 선형 부분공간은 벡터 직선(vector line)입니다. 차원 2의 선형 부분공간은 벡터 평면(vector plane)입니다. 주변 공간의 기초 중 하나를 제외하고 모든 원소를 포함하는 선형 부분공간은 벡터 초평면(vector hyperplane)입니다. 유한 차원 n의 벡터 공간에서, 벡터 초평면은 그때에 차원 n – 1의 부분공간입니다.

부분 공간에 대한 짝은 몫 벡터 공간입니다. 임의의 부분공간 W ⊂ V가 주어지면, 몫 공간 V/W ("V 모듈로 W")는 다음처럼 정의됩니다: 집합으로, 그것은 v + W = {v + w : w ∈ W}으로 구성되며, 여기서 v는 V에서 임의적인 벡터입니다. 두 개의 그러한 원소 v₁ + W와 v₂ + W의 합은 (v₁ + v₂) + W이고, 스칼라 곱셈은 a · (v + W) = (a · v) + W에 의해 제공됩니다. 이 정의에서 핵심은 v₁ + W = v₂ + W인 것과 v₁과 v₂의 차이가 W 안에 놓이는 것이 필요충분(iff) 조건이라는 것입니다. 이런 식으로, 몫 공간은 부분공간 W에 포함된 정보를 "잊습니다".

선형 맵 f : V → W의 커널 ker(f)는 W에서 0에 매핑되는 벡터 v로 구성됩니다. 커널과 이미지 im(f) = {f(v) : v ∈ V}는 각각 V와 W의 부분공간입니다. 커널과 이미지의 존재는 (고정된 필드 F에 걸쳐) 벡터 공간의 카테고리가 아벨 카테고리, 즉, 수학적 대상과 아벨 그룹의 카테고리와 매우 유사하게 행동하는 그들 (카테고리) 사이의 구조-보존하는 맵의 모음이라는 명제의 일부입니다. 이 때문에, 첫 번째 동형 정리 (행렬 관련된 용어로 랭크-널러티 정리(rank–nullity theorem)라고도 불림)과 같은 많은 명제와

V / ker(f) ≡ im(f).

두 번째와 세 번째 동형 정리는 그룹(groups)에 대해 해당하는 명제와 매우 유사한 방법으로 형식화되고 입증될 수 있습니다.

중요한 예제는 위와 같이 일부 고정된 행렬 A에 대해 선형 맵 x ↦ Ax의 커널입니다. 이 맵의 커널은 Ax = 0을 만족하는 벡터 x의 부분공간이며, 이는 정확하게 A에 속하는 동차 선형 방정식의 시스템에 대한 해의 집합입니다. 이 개념은 선형 미분 방정식으로도 확장됩니다:

$a_{0}f+a_{1}{\frac {df}{dx}}+a_{2}{\frac {d^{2}f}{dx^{2}}}+\cdots +a_{n}{\frac {d^{n}f}{dx^{n}}}=0$, 여기서 계수 a_i는 역시 x에서 함수입니다.

다음 해당하는 맵에서,

$f\mapsto D(f)=\sum _{i=0}^{n}a_{i}{\frac {d^{i}f}{dx^{i}}}$,

함수 f의 도함수(derivatives)는 선형적으로 나타납니다 (예를 들어, f′′(x)²와 반대됩니다). 미분은 선형 절차이므로(즉, 상수 c에 대해 (f + g)′ = f′ + g′이고 (c·f)′ = c·f′), 이 할당은 선형이며, 선형 미분 연산자(linear differential operator)라고 불립니다. 특히, 미분 방정식 D(f) = 0에 대한 해는 (R 또는 C에 걸쳐) 벡터 공간을 형성합니다.

Direct product and direct sum

Main articles: Direct product and Direct sum of modules

벡터 공간의 직접 곱과 벡터 공간의 직접 합은 벡터 공간의 인덱싱된 가족을 새로운 벡터 공간으로 결합하는 두 가지 방법입니다.

벡터 공간 V_i 의 가족의 직접 곱 $\textstyle {\prod _{i\in I}V_{i}}$은 모든 튜플 (v_i)_{i ∈ I}의 집합으로 구성되며, 이는 V_i의 원소 v_i에서 일부 인덱스 집합 I의 각 인덱스 i에 대해 지정합니다. 덧셈과 스칼라 곱셈은 성분-별로 수행됩니다. 이 구성의 변형은 직접 합 ${\textstyle \bigoplus _{i\in I}V_{i}}$ (공동-곱(coproduct)이라고도 하고 ${\textstyle \coprod _{i\in I}V_{i}}$로 표시됨)이며, 여기서 유한하게 많은 비-영 벡터를 갖는 튜플만 허용됩니다. 만약 인덱스 집합 I이 유한이면, 두 구성은 일치하지만, 일반적으로 그것들은 다릅니다.

Tensor product

Main article: Tensor product of vector spaces

두 벡터 공간 V와 W의 텐서 곱 V ⊗_F W 또는 간단히 V ⊗ W는 선형 맵과 같은 개념을 여러 변수로 확장하는 것을 다루는 다중선형 대수(multilinear algebra)의 중심 개념 중 하나입니다. 맵 g : V × W → X는 만약 g가 변수 v와 w 모두에서 선형이면 쌍-선형(bilinear)이라고 불립니다. 즉 말하자면, 고정된 w에 대해 맵 v ↦ g(v, w)는 위와 같은 의미에서 선형이고 고정 v에 대해서도 마찬가지입니다.

텐서 곱은 다음과 같이 쌍-선형 맵 g의 보편적인 수신자인 특정 벡터 공간입니다. 그것은 텐서(tensors)라고 하는 기호의 유한 (형식적) 합으로 구성된 벡터 공간으로 정의됩니다:

v₁ ⊗ w₁ + v₂ ⊗ w₂ + ⋯ + v_n ⊗ w_n,

다음 규칙을 필요로 합니다:

a · (v ⊗ w) = (a · v) ⊗ w = v ⊗ (a · w), 여기서 a는 스칼라입니다,

(v₁ + v₂) ⊗ w = v₁ ⊗ w + v₂ ⊗ w, and

v ⊗ (w₁ + w₂) = v ⊗ w₁ + v ⊗ w₂.

Commutative diagram depicting the universal property of the tensor product.

이들 규칙은 튜플 (v, w)를 v ⊗ w로 매핑하는 V × W에서 V ⊗ W로의 매핑 f가 쌍선형임을 보장합니다. 보편성은 임의의 벡터 공간 X와 임의의 쌍선형 맵 g : V × W → X가 주어지면, 점선 화살표를 갖는 다이어그램에 표시된 고유한 맵 u가 존재하며, f와 합성(composition)은 g: u(v ⊗ w) = g(v, w)와 같습니다. 이것은 텐서 곱의 보편적 속성(universal property)이라고 하며, 고급 추상 대수학에서 많이 사용되는 이 대상에서 또는 대상으로의 맵을 지정함으로써 대상을 간접적으로 정의하는 방법의 예시입니다.

Vector spaces with additional structure

선형 대수의 관점에서, 벡터 공간은 임의의 벡터 공간이 그것의 차원에 의해, 동형까지, 특성화되는 한 완전하게 이해됩니다. 어쨌든, 벡터 공간 자체는 함수의 수열이 또 다른 함수로 수렴하는지 여부—해석학에 중요한—문제를 처리하기 위한 프레임워크를 제공하지 않습니다. 마찬가지로, 선형 대수는 무한 급수(infinite series)를 다루기에 적합하지 않은데, 왜냐하면 덧셈 연산은 유한하게 많은 항만 더해질 수 있기 때문입니다. 그러므로, 함수형 해석학(functional analysis)의 필요성은 추가적인 구조를 고려하는 것을 요구합니다.

벡터 공간은 일부 벡터가 비교될 수 있는 부분 순서(partial order) ≤가 주어질 수 있습니다. 예를 들어, n-차원 실수 공간 Rⁿ은 벡터를 성분-별로 비교함으로써 순서화될 수 있습니다. 순서화된 벡터 공간(Ordered vector spaces), 예를 들어 리스 공간(Riesz spaces)은 두 양수 함수의 차이로 함수를 표현하는 능력에 의존하는 르베그 적분(Lebesgue integration)에 대한 기본입니다:

$f=f^{+}-f^{-}$,

여기서 $f^{+}$는 $f$의 양수 부분을 나타내고 and $f^{-}$는 음수 부분입니다.

Normed vector spaces and inner product spaces

Main articles: Normed vector space and Inner product space

벡터를 "측정하는 것"은 벡터의 길이를 측정하는 데이터, 노름(norm)을 지정함으로써, 또는 벡터 사이의 각도를 측정하는 안의 곱(inner product)에 의해 수행됩니다. 노름과 안의 곱은 각각 $|\mathbf {v} |$과 $\langle \mathbf {v} ,\mathbf {w} \rangle$로 표시됩니다. 안의 곱의 데이터는 벡터의 길이가 결합된 노름 ${\textstyle |\mathbf {v} |:={\sqrt {\langle \mathbf {v} ,\mathbf {v} \rangle }}}$을 정의함으로써 역시 정의될 수 있음을 수반합니다. 그러한 데이터를 갖춘 벡터 공간은 각각 노름 벡터 공간과 안의 곱 공간으로 알려져 있습니다.

좌표 공간 Fⁿ은 다음과 같은 표준 점 곱(dot product)을 갖출 수 있습니다:

$\langle \mathbf {x} ,\mathbf {y} \rangle =\mathbf {x} \cdot \mathbf {y} =x_{1}y_{1}+\cdots +x_{n}y_{n}.$

R²에서, 이것은 코사인 법칙(law of cosines)에 의해 두 벡터 x와 y 사이의 각도의 공통적인 개념을 반영합니다:

$\mathbf {x} \cdot \mathbf {y} =\cos \left(\angle (\mathbf {x} ,\mathbf {y} )\right)\cdot |\mathbf {x} |\cdot |\mathbf {y} |.$

이것 때문에, $\langle \mathbf {x} ,\mathbf {y} \rangle =0$를 만족시키는 두 벡터는 직교(orthogonal)라고 불립니다. 표준 점 곱의 중요한 변형은 민코프스키 공간(Minkowski space): 다음 로렌츠 곱이 부여된 R⁴에서 사용됩니다:

$\langle \mathbf {x} |\mathbf {y} \rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}.$

표준 점 곱과 대조적으로, 그것은 양수 한정(positive definite)이 아닙니다: $\langle \mathbf {x} |\mathbf {x} \rangle$도 예를 들어 $\mathbf {x} =(0,0,0,1)$에 대해 음수 값을 취합니다. 세 개의 공간-차원과 대조적으로 시간에 해당하는 네 번째 좌표를 골라내면 특수 상대성(special relativity)의 수학적 처리에 대해 그것을 유용하게 만듭니다.

Topological vector spaces

Main article: Topological vector space

수렴 질문은 서로 가까운 것인 원소에 대해 이야기할 수 있는 구조, 호환-가능 토폴로지를 운반하는 벡터 공간 V를 고려함으로써 처리됩니다. 여기서 호환-가능은 덧셈과 스칼라 곱셈이 연속 맵(continuous maps)이어야 함을 의미합니다. 대략적으로, 만약 V에서 x와 y, 및 F에서 a가 경계진 양만큼 변하면, x + y와 ax도 마찬가지입니다. 스칼라가 변경되는 양을 지정하는 것을 이해하기 위해, 필드 F도 이 문맥에서 토폴로지를 수행해야 합니다; 공통적인 선택은 실수 또는 복소수입니다.

이러한 토폴로지적 벡터 공간에서, 벡터의 급수(series)를 고려할 수 있습니다. 다음 무한 합(infinite sum)은

$\sum _{i=0}^{\infty }f_{i}$

V의 원소의 수열 (f_i)_i∈N의 해당하는 유한 부분 합의 극한(limit)을 나타냅니다. 예를 들어, f_i는 일부 함수 공간(function space) V에 속하는 (실수 또는 복소수) 함수일 수 있으며, 이 경우에서 급수는 함수 급수(function series)입니다. 급수의 수렴의 모드(mode of convergence)는 함수 공간에 부과된 토폴로지에 따라 다릅니다. 그러한 경우에서, 점-별 수렴(pointwise convergence)과 균등 수렴(uniform convergence)이 두 가지 대표적인 예제입니다.

Unit "spheres" in R² consist of plane vectors of norm 1. Depicted are the unit spheres in different p-norms, for p = 1, 2, and ∞. The bigger diamond depicts points of 1-norm equal to 2.

특정 무한 급수의 극한의 존재를 보장하는 방법은 임의의 코시 수열(Cauchy sequence)이 극한을 가진다는 공간으로 주의를 제한하는 것입니다; 그러한 벡터 공간은 완비(complete)라고 불립니다. 대략적으로, 벡터 공간은 그것이 모든 필요한 극한을 포함한다는 조건 아래에서 완비입니다. 예를 들어, 균등 수렴의 토폴로지(topology of uniform convergence)를 갖춘 단위 구간 [0,1] 위에 다항식의 벡터 공간은 [0,1] 위에 임의의 연속 함수가 바이어슈트라스 근사 정리(Weierstrass approximation theorem)에 의해 다항식의 수열에 의해 균등하게 근사될 수 있기 때문에 완비가 아닙니다. 대조적으로, 같은 토폴로지를 갖는 [0,1] 위에 모든 연속 함수의 공간은 완비입니다. 노름은 벡터의 수열 v_n이 v에 수렴하는 것과 다음이 필요충분 조건이라고 정의함으로써 토폴로지를 발생시킵니다:

$\lim _{n\to \infty }|\mathbf {v} _{n}-\mathbf {v} |=0.$

바나흐와 힐베르트 공간은 그것의 토폴로지가 각각 노름과 안의 곱에 의해 주어진 완비 토폴로지적 벡터 공간입니다. 함수형 해석학(functional analysis)의 핵심 부분인 그것들의 연구는 무한-차원 벡터 공간에 초점을 맞추고 있는데, 왜냐하면 유한-차원 토폴로지적 벡터 공간 위에 모든 노름이 같은 수렴의 개념을 일으키기 때문입니다. 오른쪽에 이미지는 R² 위에 1-노름과 ∞-노름의 동등성을 보여줍니다: 단위 "공"이 서로를 둘러싸기 때문에, 수열은 일 노름에서 영에 수렴하는 것과 다른 노름에서 그렇게 하는 것은 필요충분 조건입니다. 무한-차원의 경우에서, 어쨌든, 일반적으로 비-동등한 토폴로지일 수 있으며, 이는 토폴로지적 벡터 공간의 연구를 추가적인 데이터 없이 벡터 공간의 그것보다 풍부하게 만듭니다.

개념적 관점에서, 토폴로지적 벡터 공간과 관련된 모든 개념은 토폴로지와 일치해야 합니다. 예를 들어, 모든 선형 맵 (함수형이라고도 함) V → W를 고려하는 대신, 토폴로지적 벡터 공간 사이의 맵은 연속적이어야 합니다. 특히, (토폴로지적) 이중 공간 $V^{*}$은 연속 함수형 V → R (또는 C)로 구성됩니다. 기본 한–바나흐 정리(Hahn–Banach theorem)는 연속 함수형에 의해 적절한 토폴로지적 벡터 공간의 부분-공간을 분리하는 것과 관련이 있습니다.

Banach spaces

Main article: Banach space

바나흐 공간은, 스테판 바나흐(Stefan Banach)에 의해 도입되었으며, 완비 노름 벡터 공간입니다.

첫 번째 예제는 실수 엔트리 $\mathbf {x} =\left(x_{1},x_{2},\ldots ,x_{n},\ldots \right)$를 갖는 무한 벡터로 구성된 벡터 공간 $\ell ^{p}$이며, 그것의 $p$-노름 $(1\leq {p}\leq \infty )$은 다음에 의해 주어집니다:

$\left\|\mathbf {x} \right\|_{p}:=\left(\sum _{i}\left\vert x_{i}\right\vert ^{p}\right)^{\frac {1}{p}}$ for $p<\infty$   and   $\left\|\mathbf {x} \right\|_{\infty }:=\sup _{i}\left|x_{i}\right|$.

무한-차원 공간 $\ell ^{p}$의 토폴로지들은 서로 다른 $p$에 대해 동등하지 않습니다. 예를 들어, 벡터 $\mathbf {x} _{n}=\left(2^{-n},2^{-n},\ldots ,2^{-n},0,0,\ldots \right)$의 수열은, 이것에서 처음 $2^{n}$개 구성요소는 $2^{-n}$이고 다음 구성요소는 $0$이며, $p=\infty$에 대해 영 벡터(zero vector)로 수렴하지만, $p=1$에 대해 그렇지 않습니다:

$\left\Vert \mathbf {x} _{n}\right\Vert _{_{\infty }}=\sup(2^{-n},0)=2^{-n}\rightarrow 0$, but $\left\Vert \mathbf {x} _{n}\right\Vert _{1}=\sum _{i=1}^{2^{n}}2^{-n}=2^{n}\cdot 2^{-n}=1.$

더 일반적으로, 실수의 수열보다, 함수 $f\colon \Omega \to \mathbb {R}$은 다음 르베그 적분(Lebesgue integral)에 의해 위의 합을 대체하는 노름을 갖춥니다:

$\left\Vert {f}\right\Vert _{p}:=\left(\int _{\Omega }\left\vert {f}\left(x\right)\right\vert ^{p}\,{d\mu \left(x\right)}\right)^{\frac {1}{p}}.$

주어진 도메인(domain) $\Omega$ (예를 들어 구간) 위에 $\left\Vert {f}\right\Vert _{p}<\infty$를 만족시키고, 이 노름을 갖춘 적분-가능 함수(integrable functions)의 공간은 $L^{\;\!p}\left(\Omega \right)$로 표시되는 르베그 공간(Lebesgue spaces)이라고 불립니다.

이들 공간이 완비입니다. (만약 리만 적분을 대신 사용하면, 그 공간은 완비가 아니며, 이는 르베그 적분 이론에 대한 정당화로 볼 수 있습니다.) 구체적으로 이것은 $\left\Vert {f}_{n}\right\Vert _{p}<\infty$를 갖는, 다음 조건을 만족시키는 베그-적분가능 함수의 임의의 수열 $f_{1},f_{2},\ldots ,f_{n},\ldots$에 대해,

$\lim _{k,\ n\to \infty }\int _{\Omega }\left\vert {f}_{k}(x)-{f}_{n}(x)\right\vert ^{p}\,{d\mu \left(x\right)}=0$

다음을 만족하는

$\lim _{k\to \infty }\int _{\Omega }\left\vert {f}\left(x\right)-{f}_{k}\left(x\right)\right\vert ^{p}\,{d\mu \left(x\right)}=0$

벡터 공간 $L^{\;\!p}\left(\Omega \right)$에 속하는 함수 ${f}\left(x\right)$가 존재함을 의미합니다.

함수뿐만 아니라 그 도함수(derivatives)에도 경계성 조건을 부과하면 소볼레프 공간(Sobolev space)으로 이어집니다.

Hilbert spaces

Main article: Hilbert space

The succeeding snapshots show summation of 1 to 5 terms in approximating a periodic function (blue) by finite sum of sine functions (red).

완비 안의 곱 공간은 다비트 힐베르트(David Hilbert)를 기리기 위해 힐베르트 공간으로 알려져 있습니다. 힐베르트 공간 L²(Ω)는 핵심 사례이며, 다음에 의해 제공된 안의 곱을 가집니다:

$\langle f\ ,\ g\rangle =\int _{\Omega }f(x){\overline {g(x)}}\,dx,$

여기서 ${\overline {g(x)}}$는 $g(x)$의 복소 켤레(complex conjugate)를 나타냅니다.

정의에 의해, 힐베르트 공간에서 임의의 코시 수열은 극한으로 수렴합니다. 반대로, 주어진 한계 함수에 근사하는 바람직한 속성을 갖는 함수 f_n의 수열을 찾는 것도 똑같이 중요합니다. 테일러 근사화(Taylor approximation)를 가장한 초기 해석학은 다항식에 의해 미분-가능 함수(differentiable functions) f의 근사화를 수립했습니다. 스톤-바이어슈트라스 정리(Stone–Weierstrass theorem)에 의해, [a, b] 위에 모든 각 연속 함수는 다항식에 의해 원하는 만큼 근사될 수 있습니다. 삼각 함수(trigonometric functions)에 의한 유사한 근사화 기술은 공통적으로 푸리에 전개(Fourier expansion)라고 불리고, 공학에 많이 적용됩니다 (아래 참조). 더 일반적으로, 그리고 더 개념적으로, 그 정리는 "기본 함수"가 무엇인지, 또는 추상 힐베르트 공간에서, 그것들의 스팬 (즉, 유한 선형 조합과 그것들의 극한)의 클로저(closure)가 전체 공간이라는 의미에서, 어떤 기본 벡터가 힐베르트 공간 H를 생성하기에 충분한지에 대한 간단한 설명을 산출합니다. 그러한 함수의 집합은 H의 기저라고 불리며, 그 카디널리티는 힐베르트 공간 차원(Hilbert space dimension)으로 알려져 있습니다. 그 정리는 근사화 목적에 충분할 만큼 적절한 기저 함수를 나타낼 뿐만 아니라, 그람–슈미트 과정(Gram–Schmidt process)과 함께, 직교 벡터의 기저(basis of orthogonal vectors)를 구성할 수 있습니다. 그러한 직교 기저는 유한-차원 유클리드 공간(Euclidean space)에서 좌표 축의 힐베르트 공간 일반화입니다.

다양한 미분 방정식(differential equations)에 대한 해는 힐베르트 공간의 관점에서 해석될 수 있습니다. 예를 들어, 물리학과 공학에서 많은 분야는 그러한 방정식으로 이어지고 자주 특정 물리적 속성을 갖는 해가 종종 직교하는 기저 함수로 사용됩니다. 물리학의 예로서, 양자 역학(quantum mechanics)에서 시간-종속 슈뢰딩거 방정식(Schrödinger equation)은 시간에 따른 물리적 특성의 변화를 그 해가 파동함수(wavefunctions)라고 불리는 부분 미분 방정식(partial differential equation)으로 설명합니다. 에너지 또는 운동량과 같은 물리적 속성에 대해 한정된 값은 특정 (선형) 미분 연산자(differential operator)의 고윳값(eigenvalues)에 해당하고 결합된 파동함수는 고유-상태(eigenstates)라고 불립니다. 스펙트럼 정리(spectral theorem)는 이들 고유-함수와 그들 고윳값의 관점에서 함수에 작용하는 선형 컴팩트 연산자(compact operator)를 분해합니다.

Algebras over fields

Main articles: Algebra over a field and Lie algebra

A hyperbola, given by the equation x ⋅ y = 1. The coordinate ring of functions on this hyperbola is given by R[x, y] / (x · y − 1), an infinite-dimensional vector space over R.

일반 벡터 공간은 벡터 사이의 곱셈을 소유하지 않습니다. 두 벡터의 곱셈을 정의하는 추가적인 쌍-선형 연산자(bilinear operator)를 갖춘 벡터 공간은 필드에 걸쳐 대수입니다. 많은 대수는 일부 기하학적 대상의 함수에서 유래합니다: 주어진 필드에 값을 갖는 함수는 쌍-별로 곱할 수 있기 때문에, 이들 엔터티는 대수를 형성합니다. 스톤-바이어슈트라스 정리(Stone–Weierstrass theorem)는, 예를 들어, 바나흐 공간이자 대수인 바나흐 대수(Banach algebras)에 의존합니다.

교환 대수(Commutative algebra)는 위에서 소개한 하나 또는 여러 변수에서 다항식 링(rings of polynomials)을 잘 활용합니다. 이것들의 곱셈은 교환적(commutative) 및 결합적(associative) 둘 다입니다. 이들 링과 그것들의 몫(quotients)은 대수적 기하학의 기저를 형성하는데, 왜냐하면 그것들이 대수적 기하학적 대상의 함수의 링이기 때문입니다.

또 다른 중요한 예제는 교환적도 아니고 결합적도 아닌 리 대수(Lie algebras)이지만, 그렇게 하지 못하는 것은 제약 조건에 의해 제한됩니다 ([x, y]는 x와 y의 곱을 나타냅니다):

• [x, y] = −[y, x] (반-교환적(anticommutativity)), 그리고
• [x, [y, z]] + [y, [z, x]] + [z, [x, y]] = 0 (야코비 항등(Jacobi identity)).

예제는 [x, y] = xy − yx를 갖는 nxn 행렬의 벡터 공간, 두 행렬의 교환자(commutator), 및 교차 곱(cross product)을 갖춘 R³를 포함합니다.

텐서 대수(tensor algebra) T(V)는 대수를 얻기 위해 임의의 벡터 공간 V에 곱을 더하는 형식적인 방법입니다. 벡터 공간으로서, 그것은 단순 텐서(tensors)라고 불리는 기호에 의해 스팬됩니다:

v₁ ⊗ v₂ ⊗ ⋯ ⊗ v_n, 여기서 차수(degree) n은 변합니다.

곱셈은 그러한 기호를 연쇄하고, 덧셈 아래에서 분배 법칙(distributive law)을 부과하고, 스칼라 곱셈이 위에서 도입한 두 벡터 공간의 텐서 곱과 거의 같은 방법으로 텐서 곱 ⊗과 교환함을 요구함으로써 주어집니다.  일반적으로, v₁ ⊗ v₂과 v₂ ⊗ v₁ 사이에는 관계가 없습니다. 두 개의 그러한 원소를 같도록 강제하면 대칭 대수(symmetric algebra)로 이어지고, 반면에 v₁ ⊗ v₂ = − v₂ ⊗ v₁를 강제하면 외부 대수(exterior algebra)를 산출합니다.

필드 F가 명시적으로 언급될 때, 사용되는 공통적인 용어는 F-대수입니다.

Related structures

Vector bundles

Main articles: Vector bundle and Tangent bundle

A Möbius strip. Locally, it looks like U × R.

벡터 다발(vector bundle)은 토폴로지적 공간(topological space) X에 의해 연속적으로 매개변수화된 벡터 공간의 가족입니다. 더 정확하게, X에 걸쳐 벡터 다발은 X에서 모든 각 x에 대해, 올(fiber) π⁻¹(x)가 벡터 공간임을 만족하는 다음 연속 맵을 갖춘 토폴로지적 공간 E입니다:

π : E → X

경우 dim V = 1가 직선 다발(line bundle)이라고 불립니다. 임의의 벡터 공간 V에 대해, 투영 X × V → X은 곱 X × V를 "자명한" 벡터 다발로 만듭니다. X에 걸쳐 벡터 다발은 X와 일부 (고정된) 벡터 공간 V의 지역적(locally) 곱이어야 합니다: X에서 모든 각 x에 대해, π의 π⁻¹(U)로의 제한은 자명한 다발 U × V → U와 동형적임을 만족하는 x의 이웃(neighborhood) U가 있습니다. 지역적으로 자명한 특성에도 불구하고, 벡터 다발은 (놓여있는 공간 X의 모양에 따라) 크게 "비틀릴" 수 있습니다 (즉, 다발은 자명한 다발 X × V일 필요는 없습니다—전역적으로 동형일 필요는 없습니다). 예를 들어, 뫼비우스 띠(Möbius strip)는 (열린 구간을 실수 직선으로 식별함으로써) 원 S¹에 걸쳐 직선 다발로 볼 수 있습니다. 그것은, 어쨌든, 원기둥 S¹ × R과 다른데, 왜냐하면 후자는 방향-가능(orientable)이고 반면 전자는 그렇지 않기 때문입니다.

특정 벡터 다발의 속성은 놓여있는 토폴로지적 공간에 대한 정보를 제공합니다. 예를 들어, 접 다발(tangent bundle)은 미분-가능 매니폴드의 점에 의해 매개변수화된 접 공간(tangent spaces)의 모음으로 구성됩니다. 원 S¹의 접 다발은 S¹ × R과 전역적으로 동형적인데, 왜냐하면 S¹ 위에 전역 비-영 벡터 필드(vector field)가 있기 때문입니다. 대조적으로, 털난 공 정리(hairy ball theorem)에 의해, 모든 곳이 비-영인 2-구 S² 위에 (접) 벡터 필드가 없습니다. K-이론은 일부 토폴로지적 공간에 걸쳐 모든 벡터 다발의 동형 클래스를 연구합니다. 토폴로지적 및 기하학적 통찰력을 심화하는 것 외에도, 그것은 유한-차원 실수 나눗셈 대수: R, C, 쿼터니언 H, 및 옥토니언 O의 분류와 같은 순수하게 대수적 결과를 가집니다.

미분-가능 매니폴드의 코탄젠트 다발(cotangent bundle)은 다양체의 모든 각 점에서 접 공간의 이중, 코탄젠트 공간(cotangent space)으로 구성됩니다. 해당 다발의 단면(Sections)은 미분 일-형식(differential one-forms)으로 알려져 있습니다.

Modules

Main article: Module

모듈(Modules)은 벡터 공간이 필드에 대한 것이 링(rings)에 대한 것입니다: 필드 F 대신 링 R에 적용되는 같은 공리는 모듈을 산출합니다. 벡터 공간의 이론과 비교하여 모듈의 이론은 곱셈의 역(multiplicative inverses)을 가지지 않는 링 원소의 존재에 의해 복잡합니다. 예를 들어, 모듈은 Z-모듈 (즉, 아벨 그룹) Z/2Z가 보여주는 것처럼 기저를 가질 필요가 없습니다; 그렇게 하는 그것들 모듈 (모든 벡터 공간을 포함)은 자유 모듈(free modules)이라고 알려져 있습니다. 그럼에도 불구하고, 벡터 공간은 필드(field)인 링에 걸쳐 모듈(module)로 간결하게 정의될 수 있으며, 원소는 벡터라고 불립니다. 일부 저자는 나눗셈 링(division ring)에 걸쳐 모듈을 의미하기 위해 벡터 공간이라는 용어를 사용합니다. 스펙트럼(spectrum)을 통한 교환 링의 대수-기하학적 해석은 벡터 다발에 대한 대수적 짝, 지역적으로 자유 모듈(locally free modules)과 같은 개념의 개발을 허용합니다.

Affine and projective spaces

Main articles: Affine space and Projective space

An affine plane (light blue) in R³. It is a two-dimensional subspace shifted by a vector x (red).

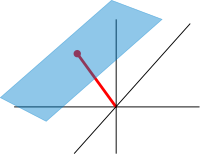
대략적으로, 아핀 공간은 그것의 원점이 지정되지 않은 벡터 공간입니다. 보다 정확하게, 아핀 공간은 자유 전이(free transitive) 벡터 공간 동작(action)을 갖는 집합입니다. 특히, 벡터 공간은 다음과 같은 맵에 의해 그 자체에 걸쳐 아핀 공간입니다:

V × V → V, (v, a) ↦ a + v.

만약 W가 벡터 공간이면, 아핀 부분-공간은 선형 부분-공간 V를 고정된 벡터 x ∈ W로 변환함으로써 얻은 W의 부분-집합입니다; 이 공간은 x + V에 의해 표시되고 (W에서 V의 코셋(coset)임), v ∈ V에 대해 x + v 형식의 모든 벡터로 구성됩니다. 중요한 예제는 다음 방정식에 b = 0을 설정함으로써 구할 수 있는 위의 동차 경우를 생성하는 다음 비-동차 선형 방정식 시스템의 해의 공간입니다:

Ax = b

해의 공간은 아핀 부분공간 x + V이며, 여기서 x는 방정식의 특정 해이고, V는 동차 방정식의 해의 공간 (A의 널공간(nullspace))입니다.

고정된 유한-차원 벡터 공간 V의 일-차원 부분-공간의 집합은 투영 공간(projective space)으로 알려져 있습니다; 그것은 무한대에서 교차하는 평행(parallel) 직선의 아이디어를 형식화하기 위해 사용될 수 있습니다. 그라스만(Grassmannians) 및 플래그 매니폴드(flag manifolds)는 각각 고정된 차원 k의 선형 부분-공간과 부분 공간의 플래그(flags)를 매개변수화함으로써 이를 일반화합니다.

Related concepts

Specific vectors in a vector space

• 영 벡터(Zero vector) (때때로 역시 널 벡터(null vector)라고 불리고 $\mathbf {0}$에 의해 표시됨), 벡터 공간에서 덧셈 항등원(additive identity). 노름 벡터 공간(normed vector space)에서, 노름 영의 유일한 벡터입니다. 유클리드 벡터 공간(Euclidean vector space)에서, 길이 영의 유일한 벡터입니다.
• 기저 벡터(Basis vector), 벡터 공간의 주어진 기저(basis)의 원소.
• 단위 벡터(Unit vector), 노름 벡터 공간에서 노름(norm)이 1인 벡터, 또는 길이 일의 유클리드 벡터(Euclidean vector).
• 등방성 벡터(Isotropic vector) 또는 널 벡터(null vector), 이차 형식(quadratic form)을 갖는 벡터 공간에서, 형식이 영인 비-영 벡터. 만약 널 벡터가 존재하면, 이차 형식은 등방성 이차 형식(isotropic quadratic form)이라고 말합니다.

Vectors in specific vector spaces

• 열 벡터(Column vector), 오직 하나의 열을 갖는 행렬. 고정된 숫자의 행을 갖는 열 벡터는 벡터 공간을 형성합니다.
• 행 벡터(Row vector), 오직 하나의 행을 갖는 벡터. 고정된 숫자의 열을 갖는 행 벡터는 벡터 공간을 형성합니다.
• 좌표 벡터(Coordinate vector), n 원소의 기저 위에 벡터의 좌표(coordinates)의 n-튜플. 필드(field) F에 걸쳐 벡터 공간에 대해, 이들 n-튜플은 벡터 공간 $F^{n}$을 형성합니다 (여기서 연산은 점별 덧셈과 스칼라 곱셈입니다).
• 변위 벡터(Displacement vector), 이전 위치에 관한 점의 위치에서 변화를 지정하는 벡터. 변위 벡터는 평행이동(translations)의 벡터 공간에 속합니다.
• 점의 위치 벡터(Position vector), 참조 점 (원점이라고 불림)에서 점까지의 변위 벡터. 위치 벡터는 유클리드 공간(Euclidean space) 또는 아핀 공간(affine space)에서 점의 위치를 나타냅니다.
• 속도 벡터(Velocity vector), 위치 벡터의, 시간에 관한, 도함수. 그것은 원점의 선택에 의존하지 않고, 따라서 평행이동의 벡터 공간에 속합니다.
• 유사-벡터(Pseudovector), 역시 축 벡터(axial vector)라고 불림
• 코벡터(Covector), 벡터 공간의 이중(dual)의 원소. 안의 곱 공간(inner product space)에서, 안의 곱은 공간과 그것의 이중 사이의 동형을 정의하며, 이는 코벡터와 벡터를 구별하기 어렵게 만들 수 있습니다. (비-직교적으로) 좌표를 변경할 때 구별이 분명해집니다.
• 접 벡터(Tangent vector), 곡선(curve), 표면(surface), 또는, 더 일반적으로 주어진 점에서 미분 매니폴드(differential manifold)의 접 공간(tangent space)의 원소 (이들 접 공간은 자연적으로 벡터 공간의 구조가 부여됩니다)
• 법선 벡터(Normal vector) 또는 단순히 법선(normal), 유클리드 공간으로, 또는, 보다 일반적으로, 안의 곱 공간에서, 점에서 접 공간에 수직인 벡터.
• 그래디언트(Gradient), 여러 실수 변수의 함수의 부분 도함수의 좌표 벡터. 유클리드 공간에서, 그래디언트는 스칼라 필드(scalar field)의 최대 증가의 크기와 방향을 제공합니다. 그래디언트는 수준 곡선(level curve)에 법선인 코벡터입니다.
• 4-벡터(Four-vector), 상대성의 이론(theory of relativity)에서, 민코프스키 공간(Minkowski space)이라고 불리는 사-차원 실수 벡터 공간에서 벡터.

See also

• Vector (mathematics and physics), for a list of various kinds of vectors

• Cartesian coordinate system
• Graded vector space
• Metric space
• P-vector
• Riesz–Fischer theorem
• Space (mathematics)
• Ordered vector space

References

Algebra

• Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-89871-510-1
• Blass, Andreas (1984), "Existence of bases implies the axiom of choice" (PDF), Axiomatic set theory (Boulder, Colorado, 1983), Contemporary Mathematics, vol. 31, Providence, R.I.: American Mathematical Society, pp. 31–33, MR 0763890
• Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5
• Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6
• Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
• Mac Lane, Saunders (1999), Algebra (3rd ed.), pp. 193–222, ISBN 978-0-8218-1646-2
• Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra, SIAM, ISBN 978-0-89871-454-8
• Roman, Steven (2005), Advanced Linear Algebra, Graduate Texts in Mathematics, vol. 135 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-24766-3
• Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups, CRC, ISBN 978-0-8247-9144-5
• van der Waerden, Bartel Leendert (1993), Algebra (in German) (9th ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56799-8

Analysis

• Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-13627-9
• Bourbaki, Nicolas (2004), Integration I, Berlin, New York: Springer-Verlag, ISBN 978-3-540-41129-1
• Braun, Martin (1993), Differential equations and their applications: an introduction to applied mathematics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97894-9
• BSE-3 (2001) [1994], "Tangent plane", Encyclopedia of Mathematics, EMS Press{{citation}}: CS1 maint: numeric names: authors list (link)
• Choquet, Gustave (1966), Topology, Boston, MA: Academic Press
• Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists, Courier Dover Publications, ISBN 978-0-486-69193-0
• Dudley, Richard M. (1989), Real analysis and probability, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6
• Dunham, William (2005), The Calculus Gallery, Princeton University Press, ISBN 978-0-691-09565-3
• Evans, Lawrence C. (1998), Partial differential equations, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0772-9
• Folland, Gerald B. (1992), Fourier Analysis and Its Applications, Brooks-Cole, ISBN 978-0-534-17094-3
• Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets, Texts in Applied Mathematics, New York: Springer-Verlag, ISBN 978-0-387-98485-8
• Ifeachor, Emmanuel C.; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (2nd ed.), Harlow, Essex, England: Prentice-Hall (published 2002), ISBN 978-0-201-59619-9
• Krantz, Steven G. (1999), A Panorama of Harmonic Analysis, Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 978-0-88385-031-2
• Kreyszig, Erwin (1988), Advanced Engineering Mathematics (6th ed.), New York: John Wiley & Sons, ISBN 978-0-471-85824-9
• Kreyszig, Erwin (1989), Introductory functional analysis with applications, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-50459-7, MR 0992618
• Lang, Serge (1983), Real analysis, Addison-Wesley, ISBN 978-0-201-14179-5
• Lang, Serge (1993), Real and functional analysis, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94001-4
• Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, The University series in higher mathematics, Toronto-New York–London: D. Van Nostrand Company, Inc., pp. x+190, hdl:2027/uc1.b4250788
• Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
• Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
• Treves, François (1967), Topological vector spaces, distributions and kernels, Boston, MA: Academic Press

Historical references

• Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)" (PDF), Fundamenta Mathematicae (in French), 3: 133–181, doi:10.4064/fm-3-1-133-181, ISSN 0016-2736
• Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (in German)
• Bellavitis, Giuso (1833), "Sopra alcune applicazioni di un nuovo metodo di geometria analitica", Il poligrafo giornale di scienze, lettre ed arti, 13, Verona: 53–61.
• Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (in French), Paris: Hermann
• Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica, 22 (3): 227–261, doi:10.1006/hmat.1995.1024, MR 1347828
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (in French), Chez Firmin Didot, père et fils
• Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (in German), O. Wigand, reprint: Grassmann, Hermann (2000), Kannenberg, L.C. (ed.), Extension Theory, translated by Kannenberg, Lloyd C., Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5
• Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy
• Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (in German), archived from the original on 2006-11-23
• Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica, 22 (3): 262–303, doi:10.1006/hmat.1995.1025
• Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (in Italian), Turin{{citation}}: CS1 maint: location missing publisher (link)
• Peano, G. (1901) Formulario mathematico: vct axioms via Internet Archive

Further references

• Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics, Toronto: Thomson Learning, ISBN 978-0-03-083993-1
• Atiyah, Michael Francis (1989), K-theory, Advanced Book Classics (2nd ed.), Addison-Wesley, ISBN 978-0-201-09394-0, MR 1043170
• Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64243-5
• Bourbaki, Nicolas (1989), General Topology. Chapters 1-4, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64241-1
• Coxeter, Harold Scott MacDonald (1987), Projective Geometry (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96532-1
• Eisenberg, Murray; Guy, Robert (1979), "A proof of the hairy ball theorem", The American Mathematical Monthly, 86 (7): 572–574, doi:10.2307/2320587, JSTOR 2320587
• Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, vol. 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94269-8, MR 1322960
• Goldrei, Derek (1996), Classic Set Theory: A guided independent study (1st ed.), London: Chapman and Hall, ISBN 978-0-412-60610-6
• Griffiths, David J. (1995), Introduction to Quantum Mechanics, Upper Saddle River, NJ: Prentice Hall, ISBN 978-0-13-124405-4
• Halmos, Paul R. (1974), Finite-dimensional vector spaces, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90093-3
• Halpern, James D. (Jun 1966), "Bases in Vector Spaces and the Axiom of Choice", Proceedings of the American Mathematical Society, 17 (3): 670–673, doi:10.2307/2035388, JSTOR 2035388
• Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013), Calculus : Single and Multivariable (6 ed.), John Wiley & Sons, ISBN 978-0470-88861-2
• Husemoller, Dale (1994), Fibre Bundles (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94087-8
• Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (4th ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-25907-7
• Kreyszig, Erwin (1991), Differential geometry, New York: Dover Publications, pp. xiv+352, ISBN 978-0-486-66721-8
• Kreyszig, Erwin (1999), Advanced Engineering Mathematics (8th ed.), New York: John Wiley & Sons, ISBN 978-0-471-15496-9
• Luenberger, David (1997), Optimization by vector space methods, New York: John Wiley & Sons, ISBN 978-0-471-18117-0
• Mac Lane, Saunders (1998), Categories for the Working Mathematician (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2
• Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0
• Naber, Gregory L. (2003), The geometry of Minkowski spacetime, New York: Dover Publications, ISBN 978-0-486-43235-9, MR 2044239
• Schönhage, A.; Strassen, Volker (1971), "Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)", Computing (in German), 7 (3–4): 281–292, doi:10.1007/bf02242355, ISSN 0010-485X, S2CID 9738629
• Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two), Houston, TX: Publish or Perish
• Stewart, Ian (1975), Galois Theory, Chapman and Hall Mathematics Series, London: Chapman and Hall, ISBN 978-0-412-10800-6
• Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations, Prentice Hall, ISBN 978-0-13-535732-3
• Wallace, G.K. (Feb 1992), "The JPEG still picture compression standard" (PDF), IEEE Transactions on Consumer Electronics, 38 (1): xviii–xxxiv, CiteSeerX 10.1.1.318.4292, doi:10.1109/30.125072, ISSN 0098-3063, archived from the original (PDF) on 2007-01-13, retrieved 2017-10-25
• Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.

External links

• "Vector space", Encyclopedia of Mathematics, EMS Press, 2001 [1994]