Polynomial

수학에서, 다항식(polynomial)은 오직 변수의 덧셈, 뺄셈, 곱셈 및 비-음의 정수 지수의 연산를 포함하는 변수(variable) (불확정수(indeterminates)라고도 함)와 계수(coefficient)로 구성된 표현식(expression)입니다. 단일 변수 $x$ 에 대한 다항식의 예제는 $x 2 - 4 x + 7$ 입니다. 세 변수에 대한 예제는 $x 3 + 2 xyz 2 - yz + 1$ 입니다.

다항식은 수학 및 과학 분야의 광범위한 영역에서 나타납니다. 예를 들어, 이들은 초급 단어 문제(word problems)에서부터 과학의 복잡한 문제에 이르기까지, 광범위한 문제를 코드화하는 다항 방정식을 형성하는 것에 사용됩니다; 그것들은 다항 함수(polynomial functions)를 정의하는데 사용되며, 기본 화학(chemistry) 및 물리학(physics)부터 경제학(economics) 및 사회 과학(social science)에 이르기까지 다양한 환경에서 나타납니다; 그들은 미적분(calculus) 및 수치 해석(numerical analysis)에서 다른 함수를 근사하기 위해서 사용됩니다. 고급 수학에서, 다항식은 다항식 링(polynomial rings)과 대수 다양체(algebraic varieties), 대수학(algebra)과 대수 기하학(algebraic geometry)의 중심 개념을 구성하는 것에 사용됩니다.

Etymology

단어 polynomial(다항식)은 두 개의 다른 종류의 뿌리: "많은"을 의미하는, 그리스어 poly, 그리고 라틴어 nomen, 또는 name을 결합한 것입니다. 이것은 binomial(이항식)이라는 용어에서 라틴어에서 온 bi-를 그리스어 poly-로 대체함으로써 파생되었습니다. 단어 polynomial은 17세기에 처음 사용되었습니다.^[1]

Notation and terminology

다항식에서 발생하는 $x$ 는 통상적으로 변수(variable) 또는 불확정수(indeterminate)라고 합니다. 다항식이 표현식으로 간주될 때, $x$ 는 값이 없는 고정된 기호입니다(그 값은 "불확정"입니다). 따라서 "불확정수"(interminate)라고 하는 것이 더 정확합니다. 어쨌든, 다항식에 의해 정의된 함수(function)를 고려할 때, $x$ 는 함수의 인수를 나타내며, 따라서 변수(variable)라고 불려집니다. 많은 저자들은 이 두 단어를 서로 바꾸어 가면서 사용합니다.

불확정수(indeterminates)로는 대문자를 사용하고 관련 함수의 변수(인수)에는 해당 소문자를 사용하는 것이 일반적입니다.

불확정수 $x$ 의 다항식 P가 $P$ 또는 $P(x)$ 로 공식에 나타날 수 있다는 것은 혼란스러울 수 있습니다.

보통, 다항식의 이름은 $P$ 이며, $P(x)$ 가 아닙니다. 어쨌든, 만약 $a$ 가 숫자, 변수, 다른 다항식, 또는, 더 일반적으로 표현식을 나타내는 경우에, $P(a)$ 는, 관례상, $x$ 를 $P$ 에 대입한 결과를 나타냅니다. 따라서 다항식 $P$ 는 함수를 정의합니다:

a\mapsto P(a),

이것은 $P$ 와 연관된 다항 함수입니다.

종종, 이 함수를 사용할 때, $a$ 가 숫자라고 가정합니다. 그러나 덧셈과 곱셈이 정의된 모든 도메인(모든 링(ring))에서 사용할 수 있습니다. 특히, $a$ 가 불확정수 $x$ 인 경우,이 함수에 의한 $x$ 의 상(image)은 다항식 $P$ 자체입니다( $x$ 를 $x$ 로 대체하는 것은 아무것도 바뀌지 않습니다). 다른 말로,

P(x)=P.

이 동등성은 "불확정수 $x$ 에 대한 다항식 $P$ "대신에 약어로 "다항식 $P(x)$ "를 쓰도록 허용합니다. 반면에, 불확정수의 이름을 강조할 필요가 없을 때에는, 만약 불확실성의 이름이 다항식의 각 항에 나타나지 않으면 많은 수식이 훨씬 더 간단하고 읽기 쉽습니다.

Definition

다항식은 상수(constants)와 불확정수 또는 변수로 불리는 기호로 덧셈, 곱셈 및 음이 아닌 정수 거듭제곱에 의한 지수화를 통해 만들어지는 표현(expression)입니다. 다항식에서는, 교환법칙, 결합법칙 및 덧셈과 곱셈의 분배법칙의 일반적인 특성을 적용하여, 서로 변환될 수 있는 두 식은 동일한 다항식을 정의하는 것으로 간주합니다.

단일 불확정수 $x$ 의 다항식은 다음 형식으로 항상 정리할 수 있습니다:

a_{n}x^{n}+a_{n-1}x^{n-1}+\dotsb +a_{2}x^{2}+a_{1}x+a_{0},

여기서 $a_{0},\ldots ,a_{n}$ 는 상수이고 $x$ 는 불확정수입니다. 단어 "불확정수"는, 비록 임의의 값으로 대체할 수 있을지라도, $x$ 가 특정한 값을 표현하는 것이 아님을 의미합니다. 대체하는 값과 이 대체의 결과를 연결하는 매핑은 하나의 함수(function)이며, 다항 함수로 불려집니다.

다항식은 합계 표기법(summation notation:sigma notation)을 사용하여 보다 간결하게 표현할 수 있습니다:

\sum _{k=0}^{n}a_{k}x^{k}

즉, 어떤 다항식은 0이 될 수도 있고 또는 0이 아닌 항(terms)의 유한 개의 합으로써 쓸 수도 있습니다. 각 항은 숫자—항의 계수(coefficient)^[2]로 불리는—와, 음수가 아닌 정수 거듭제곱으로 증가되는, 유한 개의 불확정수의 곱으로 구성됩니다.

Classification

어떤 항의 불확정수에 대한 지수는 그 항에서 불확정수의 차수(degree)라고 불려집니다; 항의 차수는 그 항의 불확정수들의 차수의 합이며, 그리고 다항식의 차수는 계수가 0이 아닌 임의의 항의 최대 차수입니다. $x = x 1$ 이기 때문에, 지수를 쓰지 않은 불확정수의 차수는 1입니다.

불확정수가 없는 항과 불확정수가 없는 다항식은, 각각, 상수항과 상수 다항식이라고 부릅니다.^[3] 상수항의 차수와 0이 아닌 상수 다항식의 차수는 0입니다. 0 다항식의 차수, 0(항이 없음)은 일반적으로 정의되지 않은 것으로 처리됩니다 (아래 부분을 참조하십시오).^[4]

예를 들어, 다음은 항입니다:

-5x^{2}y

계수는 $-5$ 이고, 불확정수는 $x$ 및 $y$ , $x$ 의 차수는 2, 하지만 $y$ 의 차수는 1입니다. 전체 항의 차수는 각 불확정수의 차수의 합이므로, 이 예제에서는 차수가 $2 + 1 = 3$ 입니다.

여러 항의 합을 붙인 것이 다항식입니다. 예를 들어, 다항식은 다음과 같습니다:

\underbrace {_{\,}3x^{2}} _{\begin{smallmatrix}\mathrm {term} \\\mathrm {1} \end{smallmatrix}}\underbrace {-_{\,}5x} _{\begin{smallmatrix}\mathrm {term} \\\mathrm {2} \end{smallmatrix}}\underbrace {+_{\,}4} _{\begin{smallmatrix}\mathrm {term} \\\mathrm {3} \end{smallmatrix}}.

위는 세 항으로 구성되어 있습니다. 첫 번째는 2차, 두 번째는 1차, 그리고 세 번째는 0차입니다.

작은 차수의 다항식은 특정한 이름이 주어집니다. 차수 0의 다항식은 상수 다항식(constant polynomial) 또는 단순히 상수(constant)입니다. 차수 1, 2 또는 3의 다항식은 각각 linear polynomials, quadratic polynomials 및 cubic polynomials입니다. 비록 높은 차수를 위해서는 특정 이름은 일반적으로 사용하지 않지만, quartic polynomial(4차) 그리고 quintic polynomial(5차)는 종종 사용됩니다. 차수에 대한 이름은 다항식 또는 그 항에 적용될 수 있습니다. 예를 들어, $x 2 + 2 x + 1$ 에서 $2 x$ 항은 quadratic 다항식에서 linear 항입니다.

다항식 0은, 항을 전혀 갖고 있지 않는, 영 다항식(zero polynomial)이라고 부릅니다. 다른 상수 다항식과는 다르게, 이것의 차수는 0이 아닙니다. 오히려 영 다항식의 차수는 명시적으로 정의되지 않거나 음수(−1 또는 −∞)로 정의됩니다.^[5] 이러한 규칙은 다항식의 유클리드 나눗셈(Euclidean division of polynomials)을 정의할 때 유용합니다. 영 다항식은 무한 수의 근(roots)을 갖는 유일한 다항식이기 때문에 고유합니다. 영 다항식의 그래프는, $f (x) = 0$ , $X$ -축 입니다.

둘 이상의 불확정수가 있는 다항식의 경우에, 만약 다항식은 0이 아닌 모든 항이 차수 $n$ 인 경우 차수 $n$ 의 동차(homogeneous)라고 합니다. 영 다항식은 동차이며, 그리고, 동차 다항식으로서, 그 차수는 정의되지 않습니다.^[6] 예를 들어, $x 3 y 2 + 7 x 2 y 3 - 3 x 5$ 는 차수 5의 동차입니다. 자세한 내용은, 동차 다항식(homogeneous polynomial)을 참조하십시오.

덧셈의 교환법칙은 임의의 원하는 차수로 항을 재배치하는 것에 사용될 수 있습니다. 불확정수가 한 개인 다항식에서, 항은 일반적으로 차수에 따라 순서대로 정렬됩니다; 즉, 가장 큰 차수가 먼저오는 " $x$ 의 거듭제곱에 대한 내림차순", 또는 " $x$ 의 거듭제곱에 대한 오름차순"으로 정렬됩니다. 위의 예제에서의 다항식은 $x$ 의 거듭제곱에 대한 내림차순으로 쓰였습니다. 첫 번째 항은 계수 $3$ , 불확정수 $x$ , 그리고 지수 2를 가집니다. 두 번째 항에서, 계수는 $-5$ 입니다. 세 번째 항은 상수입니다. 영 다항식이 아닌 다항식의 차수는 항 중에서 최대 차수이기 때문에, 이 다항식은 2차입니다.^[7]

같은 불확정수와 같은 거듭을 가진 두 항을 "동류항(similar terms 또는 like terms)"이라고 부르며, 이들은 분배법칙을 사용하여, 두 개의 항의 계수를 합해서 합쳐진 항의 계수가 되는, 하나의 항으로 합쳐질 수 있습니다. 이로 인해 계수가 0이 될 수도 있습니다.^[8] 다항식은 0이 아닌 계수를 갖는 항의 숫자에 따라 분류될 수 있으며, 한-항 다항식은 단항식(monomial)이라고 부르며,^[9] 두-항 다항식은 이항식(binomial)이라고 부르며, 그리고 삼-항 다항식은 삼항식(trinomial)이라고 부릅니다. "사항식(quadrinomial)"은 때때로 사-항 다항식을 위해 사용됩니다.

실수 다항식(real polynomial)은 실수(real) 계수를 가진 다항식입니다. 다항식의 인수는, 예를 들어 라플라스 변환(Laplace transform)의 s-평면(s-plane) 변수 등과 같이 엄격하게 제한적이지 않습니다. 실수 다항 함수(real polynomial function)는 실수 다항식에 의해 정의된 실수에서 실수로의 함수입니다. 비슷하게, 정수 다항식(integer polynomial)은 정수(integer) 계수를 가진 다항식, 및 복소수 다항식(complex polynomial)은 복소수(complex) 계수를 가진 다항식입니다.

하나의 불확정수의 다항식은 일변수(univariate) 다항식이라 불리며, 하나 이상의 불확정수의 다항식은 다변수 다항식(multivariate polynomial)이라고 불립니다. 두 개의 불확정수를 갖는 다항식을 이변수 다항식(bivariate polynomial)이라고 부릅니다. 이 개념은 개별적인 다항식보다 일반적으로 사용하는 다항식의 종류를 더 많이 참조합니다; 예를 들어 일변수 다항식을 사용할 때 상수 다항식을 배제하지 않습니다(예를 들어, 비-상수 다항식의 뺄셈에서 유래할 수 있음), 비록 엄밀히 말하자면 상수 다항식은 어떤 불확정수도 전혀 포함하지 않습니다. 허용되는 불확정수의 최대 숫자에 따라, 이변수(bivariate), 삼변수(trivariate) 등으로, 다변수 다항식을 더 분류할 수 있습니다. 다르게 생각해 보면, 고려 대상 객체들의 집합은 뺄셈에 의해 닫히기 때문에, 삼변수 다항식의 연구는 보통 이변수 다항식 등을 허용합니다. 또한, 허용되는 불확정수를 나열하는 것, " $x, y$ , 및 $z$ 의 다항식"이라고 말하는 것이 일반적입니다.

다항식의 평가는 각 불확정수에 숫자 값을 대입하고 표시된 곱셈과 덧셈을 수행하는 것으로 구성됩니다. 하나의 불확정수에 대한 다항식에서, 호너의 방법(Horner's method)을 사용하면, 일반적으로 평가가 더 효율적입니다(더 적은 숫자의 산술 연산 수행):

(((\dotsb ((a_{n}x+a_{n-1})x+a_{n-2})x+\dotsb +a_{3})x+a_{2})x+a_{1})x+a_{0}.

Arithmetic

다항식은, 필요하다면 순서 변경하고 동류항의 결합을 통해서, 덧셈의 결합법칙(모든 항을 하나의 합으로 그룹화함)을 사용하며 더할 수 있습니다.^[8]^[10] 예를 들어, 만약

{\begin{aligned}P&=3x^{2}-2x+5xy-2\\Q&=-3x^{2}+3x+4y^{2}+8\end{aligned}}

그 다음에

P+Q=3x^{2}-2x+5xy-2-3x^{2}+3x+4y^{2}+8

다음과 같이 간단히할 수 있습니다:

P+Q=x+5xy+4y^{2}+6

두 다항식의 곱을 항의 합으로 구하기 위해서, 분배법칙이 반복 적용되어, 하나의 다항식의 각 항이 다른 다항식의 모든 항에 곱해집니다.^[8] 예를 들어, 만약

{\begin{aligned}\color {Red}P&\color {Red}{=2x+3y+5}\\\color {Blue}Q&\color {Blue}{=2x+5y+xy+1}\end{aligned}}

그런 다음에

{\begin{array}{rccrcrcrcr}{\color {Red}{P}}{\color {Blue}{Q}}&{=}&&({\color {Red}{2x}}\cdot {\color {Blue}{2x}})&+&({\color {Red}{2x}}\cdot {\color {Blue}{5y}})&+&({\color {Red}{2x}}\cdot {\color {Blue}{xy}})&+&({\color {Red}{2x}}\cdot {\color {Blue}{1}})\\&&+&({\color {Red}{3y}}\cdot {\color {Blue}{2x}})&+&({\color {Red}{3y}}\cdot {\color {Blue}{5y}})&+&({\color {Red}{3y}}\cdot {\color {Blue}{xy}})&+&({\color {Red}{3y}}\cdot {\color {Blue}{1}})\\&&+&({\color {Red}{5}}\cdot {\color {Blue}{2x}})&+&({\color {Red}{5}}\cdot {\color {Blue}{5y}})&+&({\color {Red}{5}}\cdot {\color {Blue}{xy}})&+&({\color {Red}{5}}\cdot {\color {Blue}{1}})\end{array}}

다음과 같이 간단히할 수 있습니다:

PQ=4x^{2}+21xy+2x^{2}y+12x+15y^{2}+3xy^{2}+28y+5

다항식 평가는 1차 다항식에 의한 다항식 나눗셈(polynomial division)의 나머지를 계산하는 것에 사용할 수 있습니다, 왜냐하면 $f (x)$ 를 $(x - a)$ 로 나눈 나머지는 $f (a)$ 이기 때문입니다; 다항식의 나머지 정리(polynomial remainder theorem)를 참조하십시오. 이것은 몫이 필요하지 않을 때, 나눗셈의 일반적인 알고리듬보다 더 효율적입니다.

다항식의 합(sum)은 다항식입니다.^[4]
다항식의 곱(product)은 다항식입니다.^[4]
두 다항식의 합성(composition)은 다항식이며, 첫 번째 다항식의 변수에 두 번째 다항식을 대입함으로써 구해집니다.^[4]
다항식 $a n x n + a n-1 x n-1 + ... + a 2 x 2 + a 1 x + a 0$ 의 도함수(derivative)는 다항식 $n a n x n-1 + (n-1) a n-1 x n-2 + ... + 2 a 2 x + a 1$ 입니다. 만약 계수 집합이 정수 전체를 포함하지 않으면(예를 들어, 만약 계수가 소수(prime number) $p$ 의 정수 나머지(modulo)), $k a k$ 는 $a k$ 자체의 $k$ 번의 합으로 해석해야 합니다. 예를 들어, 정수 $p$ 의 나머지인 경우에는, $x p + 1$ 의 미분은 다항식 0입니다. 왜냐하면, $x p = x 0 = 1$ .^[11]
다항식 $a n x n + a n-1 x n-1 + ... + a 2 x 2 + a 1 x + a 0$ 의 원시 적분 또는 역도함수(antiderivate)는 다항식 $a n x n+1 /(n+1) + a n-1 x n /n + ... + a 2 x 3 /3 + a 1 x 2 /2 + a 0 x + c$ 이며, 여기서 $c$ 는 임의의 상수입니다. 예를 들어, $x 2 + 1$ 의 역도함수는 $1 / 3 x 3 + x + c$ 의 모양을 가집니다.

정수에 대한 것처럼, 다항식에 대한 나눗셈의 두 가지 종류가 고려됩니다. 다항식의 유클리드 나눗셈(Euclidean division of polynomials)은 정수의 유클리드 나눗셈(Euclidean division)을 일반화한 것입니다. 다항식의 다음 특성을 나타내는 두 개의 다항식, 몫(quotient)과 나머지(remainder)를 생성합니다: b ≠ 0인 두 다항식 a와 b가 주어지면, $a = b q + r$ 이고 $degree(r) < degree(b)$ 를 만족하는, 몫 q와 나머지 r를 갖는 다항식의 고유한 쌍이 존재합니다(여기서 다항식 0은 음의 차수를 가진다고 가정합니다). 컴퓨터뿐만 아니라 수작업으로, 이 부분은 다항식의 긴 나눗셈(polynomial long division) 알고리듬에 의해 계산될 수 있습니다.^[12]

고유한 인수분해 도메인(unique factorization domain)(예를 들어, 정수 또는 필드(field))의 계수를 갖는 모든 다항식에는 기약 다항식(irreducible polynomial)과 상수의 곱으로 작성되는 인수분해 형식이 있습니다. 인수분해된 형식은 인수의 순서와 가역 상수에 의한 곱셈에 의해 유일하게 결정됩니다. 복소수 필드(complex number)의 경우에는 기약 다항식은 선형(일차)입니다. 실수(real number)의 범위에서는, 일차 또는 이차가 될 수 있습니다. 정수와 유리수(rational number) 범위에서는 기약 다항식은 어떤 차수라도 될 수 있습니다.^[13] 예를 들어, 다음 다항식에 대해서

5x^{3}-5

실수와 정수의 범위에서 인수분해된 형태는 다음과 같습니다:

5(x-1)\left(x^{2}+x+1\right)

복소수의 범위에서 인수분해된 형태는 다음과 같습니다:

5(x-1)\left(x+{\frac {1+i{\sqrt {3}}}{2}}\right)\left(x+{\frac {1-i{\sqrt {3}}}{2}}\right)

인수분해(factorization)라고 불리는 인수분해된 형태의 계산은, 일반적으로 수작업으로 계산하기에는 너무 어렵습니다. 어쨌든, 효과적인 다항식의 인수분해(polynomial factorization) 알고리듬은 대부분의 컴퓨터 대수학 시스템(computer algebra system)에서 제공됩니다.

다항식의 공식 몫, 즉 분자와 분모가 다항식인 대수적 분수(algebraic fraction)는, "유리식(rational expression)" 또는 "유리 분수"라고 말하며, 일반적으로 다항식이 아닙니다. 그러나, 다항식을 숫자로 나누면, 다른 다항식이 됩니다. 예를 들어 $x 3 /12$ 는 $(1/12) x 3$ 과 같고 $1/12$ 는 상수이기 때문에, 다항식(다항식 그 자체로)에서 유효한 항으로 간주됩니다. 이 식이 항으로 사용될 때 계수는 $1/12$ 입니다. 비슷한 이유로, 만약 복소수 계수가 허용되면 $(2 + 3 i) x 3$ 와 같은 단일 항을 가질 수 있습니다; 비록 두 개의 인수로 확장되어야 하는 것처럼 보일지라도, 복소수 $2 + 3 i$ 는 하나의 복소수이며, 이 항의 계수입니다. 식 $1/(x 2 + 1)$ 은 비-상수 다항식에 의한 나눗셈을 포함하기 때문에 다항식이 아닙니다. 식 $(5 + y) x$ 는, 지수에 불확정수를 포함하고 있기 때문에, 다항식이 아닙니다.

뺄셈은 부호가 반대인 양의 덧셈에 의해 대체될 수 있고, 양의 정수 지수는 반복된 곱셈에 의해 대체될 수 있기 때문에, 모든 다항식은 상수와 불확정수의 덧셈과 곱셈만으로 구성될 수 있습니다.

Polynomial functions

다항 함수(polynomial function)는 다항식을 평가하는 것(evaluating)에 의해 정의될 수 있는 함수입니다. 보다 정확하게, 주어진 도메인으로부터 한 개의 인수(argument)의 함수 $f$ 는 만약 $f$ 의 도메인에서 모든 $x$ 에 대해 $f(x)$ 를 평가하는 다항식

a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{2}x^{2}+a_{1}x+a_{0}

가 존재하면, 다항 함수입니다 (여기서, $n$ 은 비-음의 정수이고 $a 0, a 1, a 2, ..., a n$ 은 상수 계수입니다).

일반적으로, 만약 달리 명시하지 않은 한, 다항 함수는 복소수(complex) 계수, 인수, 및 값을 가집니다. 특히, 실수 계수를 가진 것으로 제한된, 다항식은 복소수에서 복소수로의 함수를 정의합니다. 만약 이 함수의 도메인이 역시 실수로 제한(restriction)하면, 결과 함수는 실수에서 실수로 매핑합니다.

예를 들어, 다음과 같이 정의된, 함수 $f$

f(x)=x^{3}-x,

는 한 개의 변수의 다항 함수입니다. 여러 변수의 다항 함수는, 둘 이상의 불확정수에서 다항식을 사용하여, 비슷하게 정의되며, 예를 들어, 다음과 같은 것입니다:

f(x,y)=2x^{3}+4x^{2}y+xy^{5}+y^{2}-7.

다항 함수의 정의에 따르면, 분명히 다항식이 아니지만 그럼에도 불구하고 다항 함수를 정의하는 표현식이 있을 수 있습니다. 예제는 표현식 $\left({\sqrt {1-x^{2}}}\right)^{2}$ 이며, 이것은 구간 $[-1,1]$ 에서 다항식 $1-x^{2}$ 와 같은 값을 취하고, 따라서 두 표현은 이 구간에서 같은 다항 함수를 정의합니다.

모든 다항 함수는 연속(continuous), 미분 가능(smooth)이고, 적분 가능(entire)입니다.

Graphs

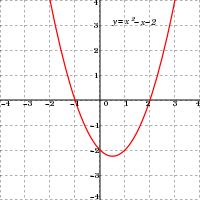
Polynomial of degree 2:
$f (x) = x 2 - x - 2$
$= (x + 1)(x - 2)$
Polynomial of degree 3:
$f (x) = x 3 /4 + 3 x 2 /4 - 3 x /2 - 2$
$= 1/4 (x + 4)(x + 1)(x - 2)$
Polynomial of degree 4:
$f (x) = 1/14 (x + 4)(x + 1)(x - 1)(x - 3) + 0.5$
Polynomial of degree 5:
$f (x) = 1/20 (x + 4)(x + 2)(x + 1 )(x - 1) (x - 3)$ $+ 2$
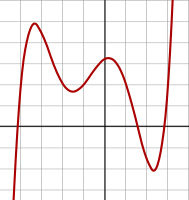
Polynomial of degree 6:
$f (x) = 1/100 (x 6 - 2 x 5 - 26 x 4 + 28 x 3$
$+ 145 x 2 - 26 x - 80)$
Polynomial of degree 7:
$f (x) = (x - 3)(x - 2)(x - 1)(x)(x + 1)(x + 2)$
$(x + 3)$

실수 변수를 갖는 다항 함수는 그래프(graph)로 나타낼 수 있습니다.

영 다항식의 그래프

f (x) = 0

는

x

-축입니다.

0차 다항식의 그래프

f (x) = a 0

, 여기서

a 0 \neq 0

,

는

y -절편 a 0

인 수평인 직선입니다.

1차 다항식의 그래프 (또는 선형 함수)

f (x) = a 0 + a 1 x

, 여기서

a 1 \neq 0

,

는

y -절편 a 0

그리고 기울기(slope)

a 1

를 갖는 사선입니다.

2차 다항식의 그래프

f (x) = a 0 + a 1 x + a 2 x 2

, 여기서

a 2 \neq 0

는 포물선(parabola)입니다.

3차 다항식의 그래프

f (x) = a 0 + a 1 x + a 2 x 2 + a 3 x 3

, 여기서

a 3 \neq 0

는 3차 곡선(cubic curve)입니다.

2차 이상인 다항식의 그래프

f (x) = a 0 + a 1 x + a 2 x 2 + ... + a n x n

, 여기서

a n \neq 0 and n \geq 2

는 연속인 비-선형 곡선입니다.

상수가 아닌 다항 함수는, 변수가 무한히 증가(절댓값으로 고려)할 때 무한대로 가는 경향(tends to infinity)이 있습니다. 만약 차수가 1보다 크면, 그래프는 어떤 점근선(asymptote)도 갖지 않습니다. 그것에는 수직 방향으로 두 개의 포물선 가지(parabolic branch)가 있습니다(한 개는 양의 x에 대한 가지이고, 다른 것은 음의 x에 대한 가지)

다항 그래프는 절편, 기울기, 오목(볼록), 그리고 끝점 경향을 사용하여 미적분학에서 분석됩니다.

Equations

다항 방정식(polynomial equation), 또는 대수 방정식(algebraic equation)은 다음의 형태의 방정식입니다^[14]:

a_{n}x^{n}+a_{n-1}x^{n-1}+\dotsb +a_{2}x^{2}+a_{1}x+a_{0}=0

예를 들어,

3x^{2}+4x-5=0

은 다항 방정식입니다.

방정식을 고려할 때, 다항식의 불확정수(변수)는 역시 미지수(unknown)라고도 하며, 방정식을 참으로 만드는 미지수의 값을 해(solutions)라고 합니다(일반적으로 하나 이상의 해가 존재할 수 있습니다). 다항 방정식은 $(x + y)(x - y) = x 2 - y 2$ 와 같은 다항 항등식(identity)과는 대비되는데, 여기서 두 표현식은 같은 다항식의 다른 형태를 나타내고, 결과적으로 두 다항식에 대한 어떠한 평가도 같은 값을 항상 가집니다.

초등 대수학에서, 한 변수에 대한 모든 일차 및 이차 다항 방정식을 풀기 위해서 근의 공식(quadratic formula)와 같은 방법들을 배웁니다. 또한, 삼차(cubic) 및 사차 방정식(quartic equations)에 대한 공식이 있습니다. 더 높은 차수에 대해서는, 아벨-루피니 정리(Abel-Ruffini theorem)는 근의 일반적인 공식이 존재할 수 없다고 단언합니다. 그러나, 근-찾기 알고리듬(root-finding algorithm)은 차수에 상관없이 다항식의 근을 수치로 근사하는 것에 사용됩니다.

실수 계수를 갖는 다항식의 실수 해의 개수는 차수를 초과할 수 없으며, 그리고 복소수(complex) 해는 중복도(multiplicity)을 각각 계산(중복되는 해를 중복 횟수만큼 계산)하는 경우에는 차수와 동일합니다. 이 사실을 대수학의 기본 정리(fundamental theorem of algebra)라고 합니다.

Solving equations

불확정수 $x$ 에 대한 모든 다항식 $P$ 는 함수(function) $x\mapsto P(x)$ 를 정의하며, $P$ 에 대응하는 다항 함수(polynomial function)라고 부릅니다; 방정식 $P (x) = 0$ 은 $P$ 에 대응하는 다항 방정식(polynomial equation)입니다. 이러한 방정식의 해는 방정식의 근(roots)이라고 부르며, 또는 대응 함수의 0의 값들입니다(이들은 함수의 그래프가 $x$ -축과 만나는 점들에 대응됩니다).

숫자 $a$ 는 다항식 $P$ 의 근인 것과 $P$ 가 선형 다항식(linear polynomial) $x - a$ 로 나누어지는 것은 서로간의 필요충분조건이고, 즉, $P = (x - a) Q$ 를 만족하는 다른 다항식 $Q$ 가 존재합니다.

$P$ 는 $x - a$ 에 의해 두번 이상 나누어질 수 있습니다: 만약 $P$ 가 $(x - a) 2$ 로 나누어질 때, $a$ 를 $P$ 의 (다)중 근(multiple root)이라고 부르고, 그렇지 않으면 $a$ 는 $P$ 의 (단순) 근(simple root)라고 부릅니다. 만약 $P$ 가 0이 아닌 다항식이면, $(x - a) m$ 이 $P$ 를 나눌 수 있는 가장 큰 거듭제곱 $m$ 이 있고, 이를 $P$ 에 대한 근 $a$ 의 중복도(multiplicity)라고 부릅니다. $P$ 가 영 다항식일 때, 대응 다항 방정식은 사소한 것이고, 이 경우는 보통 근을 고려할 때 배제합니다. 왜냐하면, 위의 정의대로 라면, 모든 숫자가 영 다항식의 근이므로, 다중도를 정의할 수 없습니다. 이런 예외가 생김으로 인해서, $P$ 의 근의 개수는, 비록 다중도를 각각 센다고 하더라도, $P$ 의 차수를 초과할 수 없습니다.^[15] 다항식의 계수와 그의 근 사이의 관계는 Vieta의 공식(Vieta's formulas)에 의해 설명됩니다.

일부 다항식은, $x 2 + 1$ 와 같은 것은, 실수(real number)에서는 어떤 근도 없습니다. 그러나, 만약 해에 허용되는 집합이 복소수(complex number)로 확장되면, 모든 비-상수 다항식은 적어도 하나의 근을 가집니다; 이것이 대수학의 기본 정리(fundamental theorem of algebra)입니다. 인수 $x - a$ 에 의해 연속적으로 나눔으로써, 복소수 계수를 갖는 다항식은 이러한 일차인 인수의 곱들과 상수(최고차항의 계수)의 곱으로 쓸 수 있으며; 결과적으로, 그들의 다중도를 함께 센 (복소수) 근의 개수는 정확히 다항식의 차수와 동일합니다.

방정식을 푸는 것에 대한 의미는 여러 가지가 있을 수 있습니다. 해를 명시적인 숫자로 표현하기를 원할 수도 있습니다; 예를 들어, $2 x - 1 = 0$ 의 유일한 해는 $1/2$ 입니다. 불행하게도, 일반적으로 이것은 차수가 1보다 큰 방정식에 대해서는 불가능하며, 고대로부터, 수학자들은 해를 대수적인 표현(algebraic expression)으로 나타내기 위해서 지속적으로 연구해 왔습니다; 예를 들어 황금비율(golden ratio) $(1+{\sqrt {5}})/2$ 은 $x^{2}-x-1=0$ 의 유일한 양의 해입니다. 고대에는, 일차와 이차에서만 성공했습니다. 이차 방정식(quadratic equation)의 경우에는, 이차 방정식의 근의 공식(quadratic formula)은 이런 해의 표현을 제공합니다. 16세기 이후로, 유사한 공식들 (이제곱근에다가 삼제곱근을 사용한 것), 그러나 삼차와 사차 방정식에 대해서는 월씬 더 복잡합니다(삼차 방정식(cubic equation) 및 사차 방정식(quartic equation)을 참조하십시오). 그러나 5차 이상을 위한 공식은 수 세기 동안에 연구자들을 빠져 나갔습니다. 1824년에, Niels Henrik Abel은, 오직 산술 연산과 $n$ 제곱근만을 포함하는, (유한한) 수식으로 해를 표현할 수 없는 5차 방정식이 있다는 놀라운 결과를 증명했습니다(Abel–Ruffini 정리을 참조하십시오). 1830년에, Évariste Galois는 4보다 높은 차수의 방정식은 $n$ 제곱근들에 의해 해결될 수 없다는 것을 증명했으며, 각 방정식에 대해서 $n$ 제곱근들에 의해 해결될 수 있는 여부를 결정할 수 있고, 만약 그렇다면, 해글 구할 수 있습니다. 이 결과는, 현대 대수학의 중요한 두 갈래인, Galois 이론과 그룹 이론(group theory)의 시작을 낳았습니다. Galois는 자신의 방법에 의해 암시된 계산은 실용적이지 못하다고 지적했습니다. 그럼에도 불구하고 5차와 6차의 풀이 가능한 방정식에 대한 공식이 발표되었습니다(5차 함수(quintic function)와 6차 방정식(sextic equation)을 참조하십시오).

근에 대한 대수 표현식이 없을 때, 그리고 그러한 대수 표현식이 존재하지만 사용하기에는 너무 복잡할 때에는, 유일한 해결책은 수치적 근사치(numerical approximationa)를 계산하는 것입니다.^[16] 이를 위한 많은 방법이 있습니다; 일부는 다항식으로 제한되며 다른 것은 임의의 연속 함수(continuous function)에 적용될 수 있습니다. 가장 효율적인 알고리듬(algorithm)은 1,000 차수가 넘는 다항식 방정식을 (컴퓨터(computer)를 이용해서) 쉽게 풀 수 있습니다(근-찾기 알고리듬(Root-finding algorithm)을 참조하십시오).

둘 이상의 불확성수가 있는 다항식에 대해서는, 다항식 함수의 값이 0을 만족하는 변수의 값의 조합은 일반적으로 "근(roots)" 대신에 영(zeros)이라고 부릅니다. 다항식의 근(zeros)의 집합의 연구는 대수 기하학(algebraic geometry)의 목적입니다. 여러 개의 미지수가 있는 다항식 방정식 근 집합에 대해서는, 유한 수의 복소수(complex) 해가 있는지 여부를 결정하는 알고리듬(algorithm)이 있으며, 그리고, 만약 이 숫자가 유한하면, 해를 계산합니다. 다항 방정식의 시스템(System of polynomial equations)을 참조하십시오.

모든 다항 방정식이 차수 1인 특수한 경우를 선형 방정식 시스템(system of linear equations)이라고 하며, 이를 위해, 고전적인 가우스 소거법(Gaussian elimination)을 비롯한, 다양한 해법(solution methods)의 다른 범위가 존재합니다.

오직 정수로 된 해에 관심이 있는 다항 방정식은 디오판토스 방정식(Diophantine equation)이라고 부릅니다. 디오판토스 방정식을 푸는 것은 일반적으로 매우 어려운 작업입니다. 그것들을 해결하기 위한 어떤 일반적인 알고리듬도 있을 수 없다는 것이 입증되었으며, 그리고 심지어 해집합이 비어 있는지 여부를 결정할 수 없다는 것이 입증되었습니다(힐베르트의 10번째 문제(Hilbert's tenth problem)를 참조하십시오.) 지난 50년 동안 해결된 가장 유명한 문제중 일부는, 페르마의 마지막 정리(Fermat's Last Theorem)과 같은, 디오판토스 방정식과 관련이 있습니다.

Generalizations

다항식의 개념에 대한 몇가지 일반화가 있습니다.

Trigonometric polynomials

삼각 다항식(trigonometric polynomial)은 하나 이상의 자연수(natural number) 값을 취하는 n과 함께 sin(nx) 및 cos(nx) 함수(functions)의 유한 선형 조합(linear combination)입니다.^[17] 계수는 실수 값 함수로써 실수로 간주할 수 있습니다.

만약 sin(nx)와 cos(nx)가 sin(x)와 cos(x)의 항으로 확장되면, 삼각 다항식은 sin(x)와 cos(x)의 다항식이 됩니다(여러-각도 공식(Multiple-angle formulae)을 사용해서). 반대로, sin(x) 및 cos(x)의 모든 다항식은 곱을 합으로 바꾸는 항등성(Product-to-sum identities)를 사용하여 함수 sin(nx) 및 cos(nx)의 선형 조합으로 변환될 수 있습니다. 이러한 동등성은 왜 선형 조합이 다항식이라고 부리워지는 것에 대한 이유를 설명합니다.

복소수 계수(complex coefficients)의 경우에, 그러한 함수와 유한 푸리에 급수(Fourier series) 사이에 차이가 없습니다.

삼각 다항식은 널리 사용되며, 예를 들어 주기 함수(periodic function)의 보간법(interpolation)에 적용되는 삼각 보간법(trigonometric interpolation)에 사용됩니다. 또한, 이산 푸리에 변환(discrete Fourier transform)에도 사용됩니다.

Matrix polynomials

행렬 다항식은 정방 행렬(정사각 행렬)이 변수인 다항식입니다.^[18] 다음처럼 보통의 스칼라-값 다항식이 주어졌을 때,

P(x)=\sum _{i=0}^{n}{a_{i}x^{i}}=a_{0}+a_{1}x+a_{2}x^{2}+\cdots +a_{n}x^{n},

이러한 다항식이 행렬 A에 대해 평가되면,

P(A)=\sum _{i=0}^{n}{a_{i}A^{i}}=a_{0}I+a_{1}A+a_{2}A^{2}+\cdots +a_{n}A^{n},

여기서 I는 항등 행렬(identity matrix)입니다.

행렬 다항 방정식(matrix polynomial equation)은 두 행렬 다항식 사이의 동치이며, 문제에서 주어진 특정 행렬에 대해 유지됩니다. 행렬 다항식 항등식(matrix polynomial identity)은 특정 행렬 링(matrix ring) M_n(R)에서 모든 행렬 A를 유지하는 행렬 다항 방정식입니다.

Laurent polynomials

로랑 다항식(Laurent polynomial)은 다항식과 같지만, 변수에 음수의 거듭제곱이 발생하는 경우를 허용합니다.

Rational functions

유리 분수(rational fraction)는 두 다항식의 몫(quotient) (대수 분수(algebraic fraction))입니다. 유리 분수로 다시 쓸 수 있는 임의의 대수 표현식(algebraic expression)은 유리 함수(rational function)입니다.

반면에 다항 함수는 변수의 모든 값에 대해 정의되지만, 유리 함수는 분모가 0이 아닌 변수의 값에 대해서만 정의됩니다.

유리 분수에는 로랑 다항식이 포함되지만, 분모는 불확정수의 거듭제곱으로 제한되지 않습니다.

Power series

형식적 멱급수(Formal power series)는 다항식과 유사하지만, 무한히 많은 0이 아닌 항이 발생하는 것을 허용하므로, 유한 차수를 갖지 않습니다. 일반적으로 다항식과는 다르게 명시적으로 그리고 완전하게 적어둘 수 없지만(무리수(irrational number)가 그러지 못하는 것처럼), 항을 조작하는 규칙은 다항식과 동일합니다.

또한, 비-형식적 멱급수(power series)는 다항식을 일반화하지만, 두 멱급수의 곱은 수렴하지 않을 수 있습니다.

Other examples

두 번째 변수가 첫 번째 변수에 적용된 지수 함수로 대체되는 이변수 다항식은, 예를 들어 $P (x, e x)$ , 지수 다항식(exponential polynomial)이라고 부를 수 있습니다.

Applications

Calculus

다항 함수의 간단한 구조는 다항 근사법을 사용하여 일반 함수를 분석하는 것에 매우 유용하게 만듭니다. 미적분학(calculus)의 중요한 예제는, 모든 미분-가능한 함수가 지역적으로 다항식 함수처럼 보이는, 테일러의 정리(Taylor's theorm)이며, 그리고, 실수 축의 컴팩트(compact) 구간(interval)에서 정의된 모든 연속 함수(continuous function)는 전체 구간에서 원하는 정도에 따라 다항식 함수로 근사될 수 있다는, 스톤-바이어슈트라스 정리(Stone–Weierstrass theorem)입니다.

다항 함수의 미분과 적분을 계산하는 것은 특히 간단합니다. 다항 함수에 대해서

\sum _{i=0}^{n}a_{i}x^{i}

x에 관한 미분은 다음과 같이 구해집니다:

\sum _{i=1}^{n}a_{i}ix^{i-1}

적분은 다음과 같이 구해집니다:

\sum _{i=0}^{n}{a_{i} \over i+1}x^{i+1}+c.

Abstract algebra

추상 대수학(abstract algebra)에서는, 다항식과 다항 함수를 구별합니다. 링(ring) $R$ 에 대한 하나의 불확정수 $x$ 에 있는 다항식 $f$ 는 다음과 같은 형식 표현식으로 정의됩니다:

f=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x^{1}+a_{0}x^{0}

여기서 $n$ 은 자연수이고, 계수 $a 0, . . ., a n$ 는 $R$ 의 원소이고, 그리고 $x$ 는 형식 기호이며, 그의 거듭제곱 $x i$ 는 상응하는 계수 $a i$ 에 대한 단지 자리-표시자이므로, 주어진 형식 표현식은 시퀀스 $(a 0, a 1, . . .)$ 를 인코딩하는 방법일 뿐이며, 여기서 모든 $i > n$ 에 대해 $a i = 0$ 인 $n$ 이 있습니다. 동일한 n 값을 공유하는 두 개의 다항식이 동일한 것으로 간주되는 것과 계수들의 시퀀스가 동일한 것은 서로간에 필요충분 조건입니다; 게다가 모든 다항식은, 계수가 0인 항들을 앞쪽에 더한, $n$ 의 값보다 더 큰 항들이 있는 임의의 다항식과 동일합니다. 이러한 다항식은 단순히 상응하는 계수를 더함으로써 추가됩니다(계수가 0인 항으로 확장하는 것에 대한 규칙은 이러한 계수가 존재하는지 확인하는 데 사용될 수 있습니다). 따라서 각 다항식은 $x^{i}$ 이외의 x의 모든 제곱에서 계수가 0 인 다항식으로 해석 될 경우 공식 표현식에 사용 된 용어의 합과 실제로 동일합니다. 따라서, 각 다항식은, 만약 그런 항 $a i x i$ 가 $x i$ 라기 보다는 $x$ 의 모든 거듭제곱에서 계수가 0을 갖는 다항식으로 해석된다면, 형식 표현식에 사용된 항의 합과 실제로 동일합니다. 그런 다음 곱셈을 정의하기 위해서, 분배법칙에 의해 주어진 두 항의 곱을 기술하는 것으로 충분하며, 다음과 같은 규칙이 주어집니다:

ax^{k}\;bx^{l}=abx^{k+l}

링 R의 모든 원소 a, b와 모든 자연수 k와 l에 대해서.

따라서 링 $R$ 에 있는 계수를 갖는 모든 다항식의 집합은 그 자체로 하나의 링을 형성하며, $R$ 에 대한 다항식의 링(ring of polynomials) 은 $R [x]$ 로 표시됩니다. $R$ 에서 $R [x]$ 로 $r$ 을 $rx 0$ 으로 보내는 맵은 링의 주입적 준동형이 되며, $R$ 은 $R [x]$ 의 서브-링으로 간주됩니다. 만약 $R$ 이 교환 가능(commutative)하다면 $R [x]$ 는 $R$ 에 대한 대수(algebra)입니다. 하나의 새로운 원소 x를 R에 추가하고, $x$ 가 의무적인 것 이외의 다른 관계를 만족하지 않는 링으로 최소한의 방법으로 확장하고, $R$ 의 모든 원소에 대해 교환법칙을 더함으로써(즉, $xr = rx$ ), 링 $R [x]$ 를 $R$ 에서 발생하는 것으로 생각할 수 있습니다. 이렇게 하기 위해서는, $x$ 의 모든 거듭제곱이 반드시 더해져야 하고, 선형 조합도 역시 더해져야 합니다.

다항식 링를 형성하는 것은, 아이디얼(ideals)을 인수분해함으로써 인수 링을 형성하는 것과 함께, 알려진 링에서 새로운 링를 만드는 중요한 도구입니다. 예를 들어, 복소수의 링(사실은 필드)은, 다항식 $x 2 + 1$ 의 배수 아이디얼을 인수분해함으로써 실수에 대한 다항식 링 $R [x]$ 으로 구성되어질 수 있습니다. 또 다른 예제는 유한 필드(finite field)의 구성으로, 이것도 비슷하게 진행되어 것으로, 정수 필드와 함께 계수 링 $R$ 처럼 일부 소수의 모듈로(modulo)로 시작합니다(모듈러 산술(modular arithmetic)을 참조하십시오).

만약 $R$ 이 교환 특성을 가지면, $R [x]$ 의 모든 다항식 $P$ , 정의역 및 치역이 $P$ 와 같은 다항 함수 $f$ 와 교환 가능합니다(더 일반적으로 $R$ 위에서 같은 단위(unital) 결합 대수(associative algebra)인 정의역과 치역을 취할 수 있습니다). $P$ 에서 기호 $x$ 에 대한 값 $r$ 을 (대체substitution)하여 $f (r)$ 값을 얻습니다. 다항식과 다항 함수를 구분하기 위한 한 가지 이유는 일부 링의 다른 다항식이 같은 다항 함수를 발생시킬 수 있기 때문입니다( $R$ 이 정수 모듈로 $p$ 인 예제의 경우에는 페르마의 작은 정리(Fermat's little theorem)를 참조하십시오). 이것은 $R$ 이 실수 또는 복소수일 때에는 해당되지 않으며, 두 개념이 분석(analysis)에서 항상 구별되지는 않습니다. 다항식과 다항 함수를 구별하는 더 중요한 이유는 다항식(유클리드 나눗셈(Euclidean division)와 같은)에 대한 많은 연산이 다항식이 $x$ 에 대해 상수 값으로 평가되는 것보다는 어떤 표현식으로 구성되어 있는지를 관찰해야 한다는 것입니다.

Divisibility

교환 가능한 대수학(commutative algebra:가환 대수학)에서, 연구의 주요 초점중 하나는 다항식들 사이의 나눔 가능성입니다. 만약 $R$ 이 정수 정의역(integral domain:정역)이고 $f$ 및 $g$ 가 $R [x]$ 의 다항식이라면, $f q = g$ 를 만족하는 $R [x]$ 에 다항식 $q$ 가 존재하면 $f$ 는 $g$ 를 나누거나 $f$ 를 $g$ 의 제수(divisor)라고 합니다. 모든 제로가 선형 제수(linear divisor)를 생기게 하거나, 또는 더 공식적으로, 만약 $f$ 가 $R [x]$ 의 다항식이고 $r$ 이 $f (r) = 0$ 을 만족하는 $R$ 의 원소이면, 다항식 ( $x - r$ )는 $f$ 를 나눕니다. 그 반대도 참입니다. 몫은 다항식의 나눗셈(polynomial long division)을 사용하여 계산할 수 있습니다.^[19]^[20]

만약 $F$ 가 필드이고 $f$ 와 $g$ 가 $g \neq 0$ 인 $F [x]$ 의 다항식이면, $F [x]$ 에, 다음을 만족하는, 고유한 다항식 $q$ 와 $r$ 가 있습니다:

f=q\,g+r

여기서 $r$ 의 차수는 $g$ 의 차수보다 반드시 작아야 합니다(관례에 따라 영 다항식은 음의 차수를 가집니다). 다항식 $q$ 와 $r$ 은 $f$ 와 $g$ 에 의해 유일하게 결정됩니다. 이것은 Euclidean division|유클리드 나눗셈(Euclidean division), 나머지가 있는 나눗셈 또는 다항식의 나눗셈이라고 불리며 그리고 링 $F [x]$ 가 유클리드 정의역(Euclidean domain)임을 보여줍니다.

유사하게, 프라임 다항식(prime polynomials)(더 정확하게, 기약 다항식(irreducible polynomials))은 두 개의 비-상수(non-constant) 다항식의 곱으로 분해 될 수 없는 비-영(non-zero) 다항식으로 정의될 수 있습니다. 링에 있는 계수의 경우에는, "비-상수"는 "비-상수 또는 비-역원(unit 또는 invertible element)"로 반드시 대체되어야 합니다(두 정의는 필드의 계수의 경우에는 모두 일치합니다). 임의의 다항식은 기약 다항식의 곱에 의해 가역 상수의 곱으로 분해될 수 있습니다. 만약 필드 또는 유일 인수분해 정의역(unique factorization domain)에 속하는 계수는 인수의 순서와 한 역원(그리고 같은 역원으로 역원 인수를 나눈 값)에 의한 임의의 비-역원 인수의 곱셈까지 고유합니다. 계수가 정수, 유리수 또는 유한 필드에 속할 때에는, 기약성(irreducibility)을 테스트하고 기약 다항식으로 인수분해를 계산하는 알고리듬이 있습니다(다항식의 인수분해(Factorization of polynomials)를 참조하십시오). 이러한 알고리듬은 수작업으로 계산하기에는 실용적이지 않지만, 모든 컴퓨터 대수학 시스템(computer algebra system)에서는 유용합니다. 또한 아이젠슈타인 판정법(Eisenstein's criterion)은, 일부의 경우에, 가역성을 결정하기 위해 사용될 수 있습니다.

Positional notation

십진수 시스템(decimal system)과 같은, 현대의 위치적 숫자 시스템에서, 정수를 나타내는 자릿수와 그들의 위치, 예를 들어 45는 밑수(radix) 또는 밑수에서 다항식에 대해 속기 표기법으로써, 이 경우에서, 4 × 10¹ + 5 × 10⁰입니다. 다른 예제로, 밑수 5에서, 132와 같은 자릿수 문자열은 (십진수) 숫자 1 × 5² + 3 × 5¹ + 2 × 5⁰ = 42를 나타냅니다. 이 표현은 고유합니다. b를 1보다 큰 양의 정수로 놓습니다. 그런 다음 모든 각 양의 정수 a는 다음 형식으로 고유하게 표현될 수 있습니다:

a=r_{m}b^{m}+r_{m-1}b^{m-1}+\dotsb +r_{1}b+r_{0},

여기서 m은 비-음의 정수이고 r들은 다음을 만족하는 정수입니다:

i = 0, 1, . . . , m - 1

에 대해

0 < r m < b

및

0 \leq r i < b

.^[21]

Other applications

다항식은, 스플라인(splines)의 사용에서 처럼, 다른 함수(functions)를 근사^[22]하는 역할을 합니다.

다항식은 다른 객체에 대한 정보를 인코딩하는 것에 자주 사용됩니다. 행렬의 characteristic polynomial특성 다항식(characteristic polynomial) 또는 선형 연산자는 연산자의 고윳값(eigenvalues)에 대한 정보를 포함합니다. 대수 원소(algebraic element)의 최소 다항식(minimal polynomial)은 해당 원소가 만족하는 가장 간단한 대수 관계를 기록합니다. 그래프(graph)의 색칠 다항식(chromatic polynomial)은 해당 그래프의 적절한 색칠 수를 계산합니다.

형용사로써, "다항식(polynomial)"이라는 용어는 다항식 형태로 쓰인 양이나 함수에 대해서도 사용될 수 있습니다. 예를 들어, 계산 복잡도 이론(computational complexity theory)에서 다항식 시간(polynomial time)은 알고리듬(algorithm)을 완료하는 것에 걸리는 시간이, 입력의 크기와 같은, 일부 변수의 다항식 함수에 의해 한정된다는 것을 의미합니다.

History

다항식의 근을 구하는 것, 또는 "대수 방정식을 푸는 것"은 수학에서 가장 오래된 문제 중에 하나입니다. 어쨌든, 오늘날 우리가 사용하는 훌륭하고 실용적인 표기법은 15세기에 개발되기 시작된 것입니다. 그 전에는, 방정식이 단어로 쓰였습니다. 예를 들어, 기원전 200년경 중국의 9절의 산술(Arithmetic in Nine Sections)에 대한 대수 문제는 "좋은 곡물 3곡, 평범한 곡물 2곡, 나쁜 곡물 1곡이 29두(dou)에 판매됩니다." 지금은 $3 x + 2 y + z = 29$ 로 쓸 것입니다.

History of the notation

알려진 것 중에 가장 처음으로 등호를 사용한 것은, 1557년 로버트 레코드(Robert Recorde)의 The Whetstone of Witte에 있습니다. 덧셈에 대한 기호 +, 뺄셈에 대한 기호 −, 그리고 미지수에 대한 문자의 사용은, 1544년 미카엘 스티펠(Michael Stifel)의 Arithemetica integra에 나타납니다. 1637년, La géometrie에서 르네 데카르트(René Descartes)는 다항 방정식의 그래프에 대한 개념을 도입했습니다. 그는 상수를 나타내기 위햇 알파벳의 앞부분의 문자를, 변수를 나타내기 위해서 알파벳의 끝부분의 문자를 사용하는 것을 대중화했으며, 위에서 볼 수 있듯이, 한 변수의 다항식에 대한 일반적인 형식에서 $a$ 는 상수를 나타내고 $x$ 는 변수를 나타냅니다. 또한, 데카르트는 지수를 나타내기 위해서 위-첨자의 사용을 소개했습니다.^[23]

Notes

^ See "polynomial" and "binomial", Compact Oxford English Dictionary
^ The coefficient of a term may be any number from a specified set. If that set is the set of real numbers, we speak of "polynomials over the reals". Other common kinds of polynomials are polynomials with integer coefficients, polynomials with complex coefficients, and polynomials with coefficients that are integers modulo of some prime number $p$ .
^ This terminology dates from the time when the distinction was not clear between a polynomial and the function that it defines: a constant term and a constant polynomial define constant functions.
^ ^a ^b ^c ^d Barbeau, E.J. (2003). Polynomials. Springer. pp. 1–2. ISBN 978-0-387-40627-5.
^ Weisstein, Eric W. "Zero Polynomial". MathWorld.
^ In fact, as homogeneous function, it is homogeneous of every degree
^ Edwards, Harold M. (1995). Linear Algebra. Springer. p. 78. ISBN 978-0-8176-3731-6.
^ ^a ^b ^c Edwards, Harold M. (1995). Linear Algebra. Springer. p. 47. ISBN 978-0-8176-3731-6.
^ Some authors use "monomial" to mean "monic monomial". See Knapp, Anthony W. (2007). Advanced Algebra: Along with a Companion Volume Basic Algebra. Springer. p. 457. ISBN 0-8176-4522-5.
^ Salomon, David (2006). Coding for Data and Computer Communications. Springer. p. 459. ISBN 978-0-387-23804-3.
^ Barbeau, E.J. (2003). Polynomials. Springer. pp. 64–5. ISBN 978-0-387-40627-5.
^ Peter H. Selby, Steve Slavin, Practical Algebra: A Self-Teaching Guide, 2nd Edition, Wiley, ISBN 0-471-53012-3 ISBN 978-0-471-53012-1
^ Barbeau, E.J. (2003). Polynomials. Springer. pp. 80–2. ISBN 978-0-387-40627-5.
^ Proskuryakov, I.V. (1994). "Algebraic equation". In Hazewinkel, Michiel (ed.). Encyclopaedia of Mathematics. Vol. vol. 1. Springer. ISBN 978-1-55608-010-4. {{cite book}}: |volume= has extra text (help)
^ Leung,, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. p. 134. ISBN 9789622092716.{{cite book}}: CS1 maint: extra punctuation (link)
^ McNamee, J.M. (2007). Numerical Methods for Roots of Polynomials, Part 1. Elsevier. ISBN 978-0-08-048947-6.
^ Powell, Michael J. D. (1981). Approximation Theory and Methods. Cambridge University Press. ISBN 978-0-521-29514-7.
^ Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. Vol. 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 0-89871-681-0. Zbl 1170.15300.
^ Irving, Ronald S. (2004). Integers, Polynomials, and Rings: A Course in Algebra. Springer. p. 129. ISBN 978-0-387-20172-6.
^ Jackson, Terrence H. (1995). From Polynomials to Sums of Squares. CRC Press. p. 143. ISBN 978-0-7503-0329-3.
^ McCoy (1968, p. 75)
^ de Villiers Johann, "Mathematics of Approximation", Springer, 2012, https://books.google.com/?id=l5mIro_6RlUC&printsec=frontcover
^ Howard Eves, An Introduction to the History of Mathematics, Sixth Edition, Saunders, ISBN 0-03-029558-0

References

Barbeau E.J., "Polynomials", Springer, 2003, https://books.google.com/?id=CynRMm5qTmQC&printsec=frontcover
Bronstein, "Solving Polynomial Equations: Foundations, Algorithms, and Applications", Springer, 2006, https://books.google.com/?id=aIlSmBV3yf8C&printsec=frontcover%7Cdisplay-editors=etal
Cahen Paul-Jean, Chabert Jean-Luc, "Integer-Valued Polynomials", American Mathematical Society, 1997, https://books.google.com/?id=AlAluH5is6AC&printsec=frontcover
Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556. This classical book covers most of the content of this article.
Leung Kam-tim, "Polynomials and Equations", Hong Kong University Press, 1992, https://books.google.com/?id=v5uXkwIUbC8C&printsec=frontcover%7Cdisplay-authors=etal
Mayr, K. Über die Auflösung algebraischer Gleichungssysteme durch hypergeometrische Funktionen. Monatshefte für Mathematik und Physik vol. 45, (1937) pp. 280–313.
Prasolov Victor V., "Polynomials", Springer, 2005, https://books.google.com/?id=qIJPxdwSqlcC&printsec=frontcover
Sethuraman B.A., "Rings, Fields, and Vector Spaces: An Introduction to Abstract Algebra Via Geometric Constructibility", Springer, 1997, https://books.google.com/?id=yWnTIqmUOFgC&pg=PA119
Umemura, H. Solution of algebraic equations in terms of theta constants. In D. Mumford, Tata Lectures on Theta II, Progress in Mathematics 43, Birkhäuser, Boston, 1984.
von Lindemann, F. Über die Auflösung der algebraischen Gleichungen durch transcendente Functionen. Nachrichten von der Königl. Gesellschaft der Wissenschaften, vol. 7, 1884. Polynomial solutions in terms of theta functions.
von Lindemann, F. Über die Auflösung der algebraischen Gleichungen durch transcendente Functionen II. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen, 1892 edition.

External links

"Polynomial", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
"Euler's Investigations on the Roots of Equations". Archived from the original on September 24, 2012. {{cite web}}: Unknown parameter |deadurl= ignored (|url-status= suggested) (help)
Weisstein, Eric W. "Polynomial". MathWorld.

[1] See "polynomial" and "binomial", Compact Oxford English Dictionary

[2] The coefficient of a term may be any number from a specified set. If that set is the set of real numbers, we speak of "polynomials over the reals". Other common kinds of polynomials are polynomials with integer coefficients, polynomials with complex coefficients, and polynomials with coefficients that are integers modulo of some prime number $p$ .

[3] This terminology dates from the time when the distinction was not clear between a polynomial and the function that it defines: a constant term and a constant polynomial define constant functions.

[Barbeau-2003-pp1-2-4] Barbeau, E.J. (2003). Polynomials. Springer. pp. 1–2. ISBN 978-0-387-40627-5.

[5] Weisstein, Eric W. "Zero Polynomial". MathWorld.

[6] In fact, as homogeneous function, it is homogeneous of every degree

[7] Edwards, Harold M. (1995). Linear Algebra. Springer. p. 78. ISBN 978-0-8176-3731-6.

[Edwards-1995-p47-8] Edwards, Harold M. (1995). Linear Algebra. Springer. p. 47. ISBN 978-0-8176-3731-6.

[9] Some authors use "monomial" to mean "monic monomial". See Knapp, Anthony W. (2007). Advanced Algebra: Along with a Companion Volume Basic Algebra. Springer. p. 457. ISBN 0-8176-4522-5.

[10] Salomon, David (2006). Coding for Data and Computer Communications. Springer. p. 459. ISBN 978-0-387-23804-3.

[Barbeau-2003-pp64-65-11] Barbeau, E.J. (2003). Polynomials. Springer. pp. 64–5. ISBN 978-0-387-40627-5.

[12] Peter H. Selby, Steve Slavin, Practical Algebra: A Self-Teaching Guide, 2nd Edition, Wiley, ISBN 0-471-53012-3 ISBN 978-0-471-53012-1

[Barbeau-2003-pp80-82-13] Barbeau, E.J. (2003). Polynomials. Springer. pp. 80–2. ISBN 978-0-387-40627-5.

[14] Proskuryakov, I.V. (1994). "Algebraic equation". In Hazewinkel, Michiel (ed.). Encyclopaedia of Mathematics. Vol. vol. 1. Springer. ISBN 978-1-55608-010-4. {{cite book}}: |volume= has extra text (help)

[15] Leung,, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. p. 134. ISBN 9789622092716.{{cite book}}: CS1 maint: extra punctuation (link)

[16] McNamee, J.M. (2007). Numerical Methods for Roots of Polynomials, Part 1. Elsevier. ISBN 978-0-08-048947-6.

[17] Powell, Michael J. D. (1981). Approximation Theory and Methods. Cambridge University Press. ISBN 978-0-521-29514-7.

[18] Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. Vol. 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 0-89871-681-0. Zbl 1170.15300.

[19] Irving, Ronald S. (2004). Integers, Polynomials, and Rings: A Course in Algebra. Springer. p. 129. ISBN 978-0-387-20172-6.

[20] Jackson, Terrence H. (1995). From Polynomials to Sums of Squares. CRC Press. p. 143. ISBN 978-0-7503-0329-3.

[21] McCoy (1968, p. 75)

[22] Villiers Johann, "Mathematics of Approximation", Springer, 2012, https://books.google.com/?id=l5mIro_6RlUC&printsec=frontcover

[23] Howard Eves, An Introduction to the History of Mathematics, Sixth Edition, Saunders, ISBN 0-03-029558-0

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

Etymology

Notation and terminology

Definition

Classification

Arithmetic

Polynomial functions

Graphs

Equations

Solving equations

Generalizations

Trigonometric polynomials

Matrix polynomials

Laurent polynomials

Rational functions

Power series

Other examples

Applications

Calculus

Abstract algebra

Divisibility

Positional notation

Other applications

History

History of the notation

See also

Notes

References

External links