History of mathematical notation

수학적 표기법의 역사(history of mathematical notation)^[1]는 수학적 기호(mathematical symbol)의 개시, 진행, 및 문화적 확산(cultural diffusion) 그리고 인기 또는 눈에 띄지 않음에 대한 표기법의 이동에서 직면하는 표기법의 방법의 충돌을 포함합니다. 수학적 표기법(Mathematical notation)^[2]은 수학적 방정식(equation)과 수식(formula)을 쓰기 위해 사용되는 기호(symbol)로 구성됩니다. 표기법은 양과 기호 연산자의 잘-정의된(well-defined) 표현의 집합을 일반적으로 의미합니다.^[3] 역사는 힌두–아라비아 숫자-표시(Hindu–Arabic numerals), 로마(Roman), 그리스(Greek), 히브리(Hebrew) 및 독일(German) 알파벳(alphabet)으로부터 문자, 지난 수세기에 걸쳐 수학자들에 의해 발명된 기호의 호스트를 포함합니다.

수학 표기법의 발전은 단계별로 나눌 수 있습니다.^[4]^[5] "수사학적(rhetorical)" 단계에서는 계산은 단어에 의해 수행되고 기호가 사용되지 않았습니다.^[6] "중략된(syncopated)" 단계에서는 자주 사용되는 연산과 양은 기호의 구문론적 약어로 표현되었습니다. 고대 시대로부터 포스트-클래식 연대을 관통하여,^{[note 1]} 수학적 창의성의 폭발은 종종 수세기의 정체로 이어졌습니다. 초기 현대(early modern age)가 열리고 전 세계적으로 지식이 확산됨에 따라, 수학적 발전의 서면 예제가 나타났습니다. "기호적(symbolic)" 단계에서는 표기법의 포괄적인 시스템이 수사학을 대체합니다. 16세기 이탈리아에서 시작하여, 새로운 과학적 발견과 상호 작용하는, 새로운 수학적 발전이 현재를 관통해서 계속되는 증가하는 속도로 진행되었습니다. 이 기호적 시스템은 중세의 인도 수학자들과 17세기 중엽 이래로 유럽에서 사용되어 왔고,^[7] 동 시대(contemporary era)에서 계속 발전해 왔습니다.

수학의 역사(history of mathematics)로 알려진 연구의 분야는 주로 수학에서의 발견의 기원에 대한 조사이고, 여기서 초점은, 과거의 수학적 방법과 표기법에 대한 조사입니다.

Rhetorical stage

비록 그 역사가 이오니아 학파(Ionian schools)의 역사와 함께 시작되었을지라도, 그것에 관심을 기울였던 그들 고대 그리스인(Ancient Greek)은 고대 이집트인(Ancient Egyptian)과 고대 페니키아인(Ancient Phoenicians)의 이전 조사에 크게 빚을 졌다는 것은 의심할 여지가 없습니다. 수치 표기법의 고유한 특징, 즉 지역적과 마찬가지로 본질적인 값 (산술(arithmetic))을 갖는 기호는 그의 발명의 기간에서 문명(civilization)의 상태를 의미합니다. 이 절이 헌정된 이들 초기 사람들의 수학적 성취의 우리의 지식은 불완전하고 다음의 간단한 주석은 가장 가능성이 높은 결론의 요약으로 여겨지고, 수학의 역사는 기호적 섹션과 함께 시작됩니다.

놓여있는 규칙과 개념이 추상적 구조(abstract structure)로 식별되고 정의되기 전에, 수학의 많은 분야는 실생활 문제(real world problems)의 연구와 함께 시작되었습니다. 예를 들어, 기하학은 실생활에서 거리(distance)와 넓이(area)의 계산에서 그의 기원을 가집니다; 대수학은 산술(arithmetic)에서 문제를 해결하는 방법과 함께 시작되었습니다.

기록을 남겨 온 대부분의 초기 사람들은 세는 법(numeration)과 역학(mechanics)의 일부를 알고 있었고, 일부의 사람들은 토지-측량(land-surveying)의 요소에 대해서 역시 정통하게 되었다는 것은 의심의 여지가 없습니다. 특히, 이집트인들은 기하학과 숫자에 주의를 기울였고 페니키아인들은 실용적인 산술, 부기(book-keeping), 항해(navigation) 및 토지-측량에 관심을 기울였습니다. 이들 사람들에 의해 얻어진 결과는, 특정 조건 아래에서, 여행자에 대해 접근될 수 있었던 것(Knowledge transfer) 같습니다. 그것은 아마도 이집트인과 페니키아인의 지식은 주로 관찰(observation)과 측정(measurement)의 결과였고, 많은 연대의 축적된 경험을 표현했을 것입니다.

Beginning of notation

서면 수학은 탈리 표식(tally marks)으로 표현된 숫자로 시작하는데, 각 탈리는 하나의 단위를 나타냅니다. 수치적 기호는 아마도 나무 또는 돌로 자른 획이나 노치로 구성되었고, 모든 국가에 비슷하게 이해할 수 있게 구성되었습니다.^{[note 2]} 예를 들어, 뼈에 새겨진 하나의 노치는 한 동물, 또는 사람, 또는 다른 것을 나타냅니다. (서양 역사에서 표기법이 시작되는 그들 사이에서) 소아시아의 그리스인은 빈번히 접촉하게 될 가능성이 있는 사람들은 지중해의 동부 연안(littoral)에 서식하는 사람들이었습니다: 그리고 그리스 전통은 이집트인들에게 기하학의 특별한 발전과 이집트인들 또는 페니키아인들에 대한 숫자의 과학(science of numbers)^{[note 3]}의 발전을 균등하게 할당했습니다.

고대 이집트인(Ancient Egyptians)은 신성문자에 의해 세는 법(numeration by Hieroglyphics)이었던 기호적 표기법을 가졌습니다.^[8]^[9] 이집트의 수학(Egyptian mathematics)은 일, 십, 일-백, 일-천, 일-만, 일-십만, 일-백만에 대해 기호를 가졌습니다. 더 작은 자릿수는, 그들이 힌두-아라비아 숫자 시스템일 때, 숫자의 왼쪽에 위치되었습니다. 나중에, 이집트인은 숫자를 보여주기 위해 신성문자(hieroglyphic) 스크립트 대신에 신관문자(hieratic)를 사용했습니다. 신관문자는 보다 필기체와 비슷했고 기호의 여러 그룹을 개별 그룹으로 대체했습니다. 예를 들어, 4를 나타내기 위해 사용된 4 수직 선은 하나의 수평 선으로 대체되었습니다. 이것은 린드 수학적 파피루스(Rhind Mathematical Papyrus) (기원전 c. 2000–1800)와 모스크바 수학적 파피루스(Moscow Mathematical Papyrus) (기원전 c. 1890)에서 찾아볼 수 있습니다. 이집트인이 사용했던 시스템은 지중해에서 많은 다른 문명에 의해 발견되고 변형되었습니다. 이집트인은 기본적인 연산에 대해 기호를 역시 가졌습니다: 앞으로 나아가는 다리는 덧셈을 나타내고, 뒤로 걷는 다리는 뺄셈을 나타내었습니다.

메소포타미아인(Mesopotamians)은 십의 각 거듭제곱에 대해 기호를 가졌었습니다.^[10] 나중에, 그들은 현대에서 행해진 것과 거의 정확하게 같은 방법으로 그들의 숫자를 썼습니다. 십의 각 거듭제곱에 대해 기호를 갖는 것 대신에, 그들은 그 숫자의 계수(coefficient)를 바로 넣었을 것입니다. 각 자릿수는 단지 공백에 의해 구분되었지만, 알렉산더 대왕(Alexander the Great) 시대에, 그들은 0을 나타내고 자리 표시자였었던 기호를 만들었습니다. 메소포타미아인은 육십진수(sexagesimal) 시스템, 즉 밑수 육십을 역시 사용했습니다. 그것은 시간과 각도를 측정할 때 현대에 사용되는 이 시스템입니다. 바빌로니아 수학은 1850년대 이래로 발굴된 400개 이상의 점토 태블릿으로부터 유래되었습니다.^[11] 설형문자 스크립트(Cuneiform script)에서 쓰인, 태블릿은 진흙이 촉촉한 동안 새겨졌었고, 오븐 또는 태양의 열에 열심히 구워졌습니다. 이들 중 일부는 점수가 매겨진 숙제인 것으로 보입니다. 서면 수학의 가장 최초의 증거는 고대 수메르(Sumer)인과 기원전 3000년부터 도량형학(metrology)의 시스템으로 거슬러 올라갑니다. 기원전 2500년경부터, 수메르인은 점토 태블릿 위에 곱셈 테이블(multiplication table)을 썼었고 기하학적(geometrical) 연습과 나눗셈(division) 문제를 다루었습니다. 가장 최초의 바빌론 숫자의 흔적은 역시 이시기로 거슬러 올라갑니다.^[12]

메소포타미아 점토 태블릿의 대다수는 기원전 1800년에서 기원전 1600년 사이에 작성되었고, 분수, 대수, 이차 및 삼차 방정식, 그리고 정규(regular) 역수(reciprocal) 쌍(pairs)의 계산을 포함하는 주제를 다룹니다.^[13] 태블릿은 선형(linear) 및 이차 방정식(quadratic equation)을 푸는 곱셈 테이블과 방법을 역시 포함합니다. 바빌론 태블릿 YBC 7289는 소수점 이하 다섯 자리까지 정확한 √2의 근사치를 제공합니다. 바빌론 수학은 육십진수(sexagesimal) (밑수-60) 숫자 시스템(numeral system)을 사용하여 작성되었습니다. 이것으로부터 일분에서 60초, 한시간에서 60분, 원에서 360도 (60 x 6)의 현대 사용법, 마찬가지로 도의 분수를 나타내기 위한 호의 분과 초의 사용이 파생됩니다. 수학에서 바빌론의 진보는 60은 많은 약수를 가진다는 사실에 의해 촉진되었습니다: 60의 약수의 배수인 정수의 역수는 밑수 60에서 유한한 전개를 가집니다. (십진수 산술에서, 오직 2와 5의 배수의 역수가 유한한 십진 전개를 가집니다). 또한, 이집트인, 그리스인, 로마인과는 달리, 바빌로니아인은, 십진(decimal) 시스템과 많이 비슷한, 왼쪽 열에 쓰인 자릿수가 더 큰 값을 나타내는 진정한 위치-값 시스템을 가지고 있었습니다. 그들은, 어쨌든, 소수점과 동등한 것이 없었고, 그래서 기호의 위치 값은 종종 문맥으로부터 추론되어야 했습니다.

Syncopated stage

수학의 역사는 이오니아 그리스의 그것 이전의 임의의 학파 또는 기간으로 거슬러 올라가는 객관적 확실성은 없지만 이후의 역사는 시대별로 나뉠 수 있고, 그 구분은 뚜렷하게 잘 드러납니다. 기하학의 연구와 함께 시작되었던, 그리스 수학은 시작에서부터 연역적이고 과학적이 되는 경향이 있었습니다. 기원후 4세기 이래로, 피타고라스(Pythagoras)는 피타고라스의 정리(Pythagorean theorem)를 발견한 것에 대해 공통적으로 공로를 인정받아져 왔는데, 기하학에서 정리는 직각 삼각형에서 빗변 (직각의 대변)에 대한 제곱의 넓이가 다른 두 변의 제곱의 넓이의 합과 같음을 말합니다.^{[note 5]} 고대 수학 텍스트는 이전에 언급된 고대 이집트 표기법과 Plimpton 322 (바빌로니아 수학 기원전 c. 1900)와 함께 이용할 수 있었습니다. 수학 그 자체의 주제로 수학의 연구는 기원전 6세기에 피타고라스 학파(Pythagoreans)와 함께 시작되었고, 그들은, "교육의 주제"을 의미하는, 고대 그리스어 μάθημα (mathema)로부터 용어 "수학"을 만들어 냈습니다.^[14]

플라톤(Plato)의 영향은 수학과 과학에서 특히 강하게 나타났습니다. 그는 "산술(arithmetic)", 지금 숫자 이론(number theory)으로 불리는 것과 "기호 논리학(logistic)", 지금 산술(arithmetic)이라고 불리는 것 사이의 간격을 넓힘으로써 순수(pure) 수학과 응용 수학(applied mathematics) 사이를 구별하는 것을 도왔습니다. 그리스 수학(Greek mathematics)은 (특히 증명(proofs)에서 연역적 추론과 수학적 엄격함(mathematical rigor)을 도입함으로써) 방법론을 크게 개선하고 수학의 주제를 확장했습니다.^[15] 아리스토텔레스(Aristotle)는 나중에 제외된 중간의 법칙(law of excluded middle:배중률)으로 불리는 것을 만들었습니다.

Abstract Mathematics^[16]는 산술(arithmetic)과 기하학(geometry)과 같은 특정 크기의 임의의 종에 관계없이 절대적으로 그리고 일반적으로 수여되는 크기^{[note 6]} 또는 양(quantity)을 처리하는 것입니다. 이 의미에서, 추상적 수학은 혼합 수학(mixed mathematics)에 반대하는데, 수학에서 원시적으로 고려된 양의 단순한 그리고 추상 속성, 그리고 관계는 가능성있는 대상에 적용되고, 그 수단은 유체역학(hydrostatics), 광학(optics), 및 항해(navigation)와 같은 물리적 고려 사항과 혼합됩니다.^[16]

아르키메데스(Archimedes)는 고대 수학의 가장 위대한 수학자(mathematician) 그리고 모든 시대에 걸쳐 가장 위대한 수학자 중 한 사람으로 간주됩니다.^[17]^[18] 그는 무한한 급수의 합을 갖는 포물선(parabola)의 호 아래의 넓이(area)를 계산하기 위한 소진의 방법(method of exhaustion)을 사용했고, 파이(pi)의 매우 정확한 근사를 제공했습니다.^[19] 그는 자신의 이름을 포함한 나선(spiral), 회전의 표면(surfaces of revolution:회전면)의 부피(volume)에 대한 공식 그리고 매우 큰 숫자를 표현하는 독창적인 시스템을 역시 정의했습니다.

기하학의 역사적인 발달에서, 기하학의 추상화에서 단계는 고대 그리스인에 의해 만들어졌습니다. 비록 프로클로스(Proclus)가 키오스의 히포크라테스(Hippocrates of Chios)에 의해 더 일찍 공리화(axiomatisation)를 말했을지라도— 유클리드의 원론(Euclid's Elements)은 평면 기하학의 공리의 최초의 현존하는 문서입니다.^[20] 유클리드의 원론(Elements) (기원전 c. 300)는 가장 오래된 현존하는 그리수 수학 논문 중 하나이고^{[note 7]} 알렉산드리아에서 쓰인 13권의 책; 다른 수학자들에 의해 증명된, 일부 원래 연구에 보충 설명된 정리의 모음으로 구성되어 있습니다.^{[note 8]} 문서는 정의, 공준 (정리), 전제 (정리 및 구성), 및 전제의 수학적 증명의 성대한 모음입니다. 유클리드의 첫 번째 정리(Euclid's first theorem)는 소수(prime number)의 속성을 가진 보조정리(lemma)입니다. 영향력있는 13권의 책은 유클리드 기하학, 기하학적 대수, 대수학적 시스템 및 초등 숫자 이론(초등 정수론)의 고대 그리스 버전을 다룹니다. 그것은 콰드리비엄(Quadrivium:사과)에서 어디에나 있었고 논리, 수학 및 과학의 발전에서 수단이 되었습니다.

알렉산드리아의 디오판토스(Diophantus of Alexandria)는 Arithmetica라고 불리는 일련의 책을 저술했고, 그 중 많은 책이 지금은 잃어버렸습니다. 이들 텍스트는 대수적 방정식(algebraic equation)을 해결하는 것을 다룹니다. 보에티우스(Boethius)는 산술, 기하학, 천문학 및 음악의 연구를 설명하기 위해 용어 quadrivium를 만들 때 6세기 커리큘럼에서 수학을 위한 장소를 제공했습니다. 그는 니코마코스(Nicomachus)의 Greek Introduction of Arithmetic 그리스어로부터 무료 번역, De institutione arithmetica; 역시 그리스 원천으로부터 파생된 De institutione musica; 그리고 유클리드의 원론으로부터 일련의 발췌들을 썼습니다. 그의 연구는 실용적이라기 보다는 이론적이었고, 그리스어와 아랍어의 수학적 연구의 회복까지 수학적 연구의 기초였습니다.^[21]^[22]

Acrophonic and Milesian numeration

그리스인(Greeks)은 아티 세는 법(Attic numeration)을 사용했는데,^[23] 그것은 이집트인의 시스템에 기반을 두고 나중에 로마인(Romans)에 의해 채택되고 사용되었습니다. 신성문자(hieroglyphics)에서와 같이, 그리스 숫자 시스템(Greek numerals) 1에서 4까지는 수직 직선이었습니다. 오에 대해 기호는 그리스 문자 Π (파이)였었는데, 그것은 오에 대해 그리스 단어의 문자, pente입니다. 숫자 육에서 구는 옆에 pente와 그것 다음에 수직 직선을 놓았습니다. 십은 십에 대해 단어의 문자 (Δ), deka, 백에 대해 단어로부터 문자에 의해 일백, 등에 의해 표현되었습니다.

이오니아 세는 법(Ionian numeration)은 세 개의 고풍 문자를 포함하여 그들의 전체 알파벳을 사용했습니다. 그리스인의 숫자 시스템 표기법은, 비록 현재 사용되고 있는 것보다 훨씬 덜 편리했을지라도, 완벽하게 규칙적이고 과학적인 계획에 따라 형성되었고,^[24] 로마 시스템이 완전히 적용할 수 없는 목적으로, 계산의 도구로서 견딜 수 있는 효과와 함께 사용될 수 있었습니다. 그리스인은 그들의 알파벳의 24개의 문자를 세 개의 클래스로 나눴고, 각 클래스에 다른 기호를 더함으로써, 그들은 단위, 수십, 수백을 나타내는 문자를 가졌습니다. (장 바티스트 조제프 들랑브르(Jean Baptiste Joseph Delambre)의 Astronomie Ancienne, t. ii.)

Α (α)	Β (β)	Г (γ)	Δ (δ)	Ε (ε)	Ϝ (ϝ)	Z (ζ)	H (η)	θ (θ)	I (ι)	K (κ)	Λ (λ)	Μ (μ)	Ν (ν)	Ξ (ξ)	Ο (ο)	Π (π)	Ϟ (ϟ)	Ρ (ρ)	Σ (σ)	Τ (τ)	Υ (υ)	Ф (φ)	Χ (χ)	Ψ (ψ)	Ω (ω)	Ϡ (ϡ)
1	2	3	4	5	6	7	8	9	10	20	30	40	50	60	70	80	90	100	200	300	400	500	600	700	800	900

이 시스템은, 문자 digamma (Ϝ), koppa (Ϟ) 및 sampi (Ϡ)가 퇴화하기 전에, 기원전 3세기에서 나타났습니다. 소문자가 대문자와 구별될 때, 소문자는 표기법에 대해 기호로 사용되었습니다. 일천의 배수는 그들의 앞에 스트로크와 함께 아홉 개의 숫자로 쓰였습니다: 따라서 일천은 ",α", 이천은 ",β", 등이었습니다. M (μὐριοι에 대해, "myriad"에서 처럼)은 일만에 의해 숫자를 곱하는 데 사용되었습니다. 예를 들어, 숫자 88,888,888은 M,ηωπη*ηωπη로 쓰일 것입니다.^[25]

그리스의 수학적 추론은 거의 완전히 기하학적(geometric)이었고 (비록 숫자 이론(number theory)과 같은 비-기하학적 주제에 대한 논하기 위해 종종 사용되었지만), 따라서 그리스인은 대수(algebra)적 기호에 관심이 없었습니다. 큰 예외는, 위대한 대수학자, 알렉산드리아(Alexandria)의 디오판토스(Diophantus)였습니다.^[26] 그의 Arithmetica는 방정식에서 기호를 사용하는 텍스트 중 하나였습니다. 그것은 완전히 기호적인 것은 아니었지만, 이전의 책들보다 훨씬 많았습니다. 미지의 숫자는 s라고 불렸습니다.^[27] s의 제곱은 $\Delta ^{y}$ ; 세제곱은 $K^{y}$ ; 네 번째 거듭제곱은 $\Delta ^{y}\Delta$ ; 다섯 번째 거듭제곱은 $\Delta K^{y}$ 였습니다.^[28]^{[note 9]}

Chinese mathematical notation

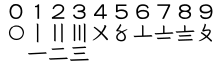
중국인은 탈리 시스템과 매우 비슷한 숫자 시스템을 사용했습니다.^[29] 숫자 1에서 4까지는 수평 직선이었습니다. 오는 두 개의 수평 직선 사이의 X였습니다; 그것은 십에 대해 로마 숫자 시스템(Roman numeral)과 거의 똑같이 보였습니다. 요즘, 소주마자 시스템(huāmǎ system)은 중국 시장 또는 전통적인 필기 송장에 가격을 표시하는 것에 대해 오직 사용됩니다.

중국인의 역사에서, 산술, 기하학, 역학, 광학, 항법, 천문학의 과학에 익숙한 사람들이 있었습니다. 중국에서 수학(Mathematics in China)은 기원전 11세기까지 독립적으로 나타났습니다.^[30] 중국인이 몇 가지 기하학적 또는 오히려 매캐니컬 머신과 함께^{[note 10]} 건축적 도구^{[note 11]}에 익숙한 것은 거의 확실한 것으로 그들은 자성 바늘의 특성을 알고 있었고; 천문학적 사건이 주기적으로 발생했다는 것을 알고 있었습니다. 그 당시 중국인들은 그들이 알고 있는 산술이나 기하학의 규칙을 분류하거나 확장했었고, 그들이 이전에 알고 있던 현상의 원인을 설명하려는 시도를 했습니다. 중국인은 독자적으로 매우 크고 음의 숫자(negative number), 십진수(decimal), 자리 값 십진 시스템, 이진 시스템(binary system), 대수학(algebra), 기하학(geometry) 및 삼각법(trigonometry)을 개발했습니다.

중국 수학(Chinese mathematics)은 자리 값 시스템(place value system)을 포함하여 초기의 공헌을 했습니다.^[31]^[32] 고대 중국인에게 알려진 기하학적 정리는 특정 경우 (즉, 변의 비율)에 적용 가능했습니다.^{[note 12]} 그것은 중첩의 준-실험의 방법으로 입증 될 수 있는 기하학적 정리가 역시 그들에게 알려져 있다는 것입니다. 산술에서 그들의 지식은 주판(swan-pan)에 의한 계산 기술과 결과를 서면으로 표현하는 능력에 한정된 것처럼 보입니다. 중국인의 초기 성취에 대한 우리의 지식은, 비록 그것이 약간이지만, 대부분의 동시대의 사람들의 경우보다 더 완전합니다. 그것은 따라서 유익한 것이고, 그것은 국가가 응용 예술에 상당한 기술을 가지고 있음을 알 수 있지만 그들의 기술이 발견된 것에 기초한 나중의 수학에 대한 우리의 지식은 부족했었다는 사실을 설명하는 데 도움이 됩니다. 기원전 254년 이전의 중국 수학에 대한 지식은 다소 단편적이고, 심지어 이 날짜 이후에도 원고의 전통은 분명하지 않습니다. 고고학적 증거가 수반되지 않은 한, 고전 시대가 시작되기 수세기 전의 시기는 일반적으로 중국 학자들에 의한 추측으로 여겨집니다.

다른 초기 사회에서와 마찬가지로, 초점은 농업 달력(calendar)과 기타 실용적인 작업을 완성하기 위한 천문학(astronomy)이었고, 형식 시스템(formal systems)을 구축하는 것에는 그렇지 않았습니다. 중국의 수학위원회(Chinese Board of Mathematics)의 업무는 연간 달력의 일년의 준비, 그것에서 규정된 날짜와 예측에 국한되었습니다. 고대 중국의 수학자들은 공리적 접근 방식을 개발하지 않았지만, 알고리듬 개발과 대수학을 발전시켰습니다. 중국 대수의 성취는 한 경(Zhu Shijie)이 넷의 미지수의 방법을 발명했을 때, 13세기에 절정에 달했습니다.

명백한 언어적 및 지리적 장벽과 마찬가지로 내용의 결과로, 중국 수학과 고대 지중해 세계의 수학의 그것은 The Nine Chapters on the Mathematical Art에 그것의 최종 형식에 도달할 때까지 어느 정도 독립적으로 발전한 것으로 추정되지만, Writings on Reckoning 및 Huainanzi는 고전 그리스 수학과 대략 동시대입니다. 적어도 로마 시대의 알려진 문화 교류를 통해 아시아 전역에서 아이디어의 일부 교환이 있었을 것 같습니다. 자주, 초기 사회의 수학의 요소가 기하학 또는 숫자 이론(number theory)과 같은 현대 수학의 가지에서 나중에 발견되는 기초적인 결과와 일치합니다. 피타고라스 정리(Pythagorean theorem)는 예를 들어, 주공단(Duke of Zhou)의 시대에 입증되었습니다. 파스칼의 삼각형(Pascal's triangle)에 대한 지식은 역시 심 괄(Shen Kuo)와 같은 파스칼(Pascal) 이전 몇 세기에 중국에 존재하는 것으로 나타났습니다.^[33]

중국에서 삼각법(trigonometry)의 상태는 송나라 (960–1279) 동안 서서히 변화하고 발전하기 시작했으며, 여기서 중국 수학자들은 달력적 과학과 천문학적 계산에서 구형 삼각법의 필요성을 크게 강조하기 시작했습니다.^[34] 폴리매쓰(polymath) 중국 과학자, 수학자 및 관료 심 괄(Shen Kuo) (1031–1095)은 현과 호의 수학적 문제를 해결하기 위해 삼각 함수를 사용했습니다.^[34] 살 레스티보(Sal Restivo)는 원의 호의 길이에서 심의 연구가 수학자이자 천문학자 곽 수경(Guo Shoujing) (1231–1316)에 의해 13세기에 개발된 구형 삼각법(spherical trigonometry)의 기초를 제공했다고 기록합니다.^[35] 역사가 L. Gauchet와 조지프 니드햄(Joseph Needham)이 말한 것처럼, 곽 수경은 달력 시스템(calendar system)과 중국 천문학(Chinese astronomy)을 향상시키기 위해 그의 계산에서 구형 삼각법(spherical trigonometry)을 사용했습니다.^[36]^[37] 중국의 수학적 과학은 13세기의 과정에서 중국에 온 구형 삼각법에 대한 지식을 가진 아랍 선교사들의 연구와 가르침을 통합할 것입니다.

Indian & Arabic numerals and notation

비록 우리의 현재 숫자 표기법의 기원은 고대였지만, 2천년 전에 힌두교 사이에서 사용되었다는 것은 의심할 여지가 없습니다. 인도 수학자(Indian mathematician), 브라마굽타(Brahmagupta)의 대수적 표기법은 중략된(syncopated) 것이었습니다. 덧셈은 숫자를 나란히 놓음으로써, 뺄셈은 피감수(subtrahend) (빼지게 되는 숫자) 위에 점을 놓음으로써, 및 나눗셈은, 우리의 표기법과 비슷하지만 막대없이, 피제수 아래에 제수를 놓음으로써 나타내었습니다. 곱셈, 전개 및 미지 양은 적절한 항의 약어로 표현되었습니다.^[38] 오늘날 전 세계적으로 사용되고있는 힌두–아라비아 숫자 시스템(Hindu–Arabic numeral system)과 그 연산의 사용의 규칙은 인도(India)에서 기원후 첫 번째 천년의 과정에 걸쳐 진화했고 이슬람 수학을 통해 서부로 전파되었을 가능성이 높습니다.^[39]^[40]

그 이름에도 불구하고, 아라비아 숫자-표시(Arabic numerals)는 인도에 뿌리를 두고 있습니다. 이 오명칭(misnomer)에 대한 이유는 유럽인들이 무하마드 이븐 무사 알-콰리즈미(Mohommed ibn-Musa al-Khwarizmi)에 의한 아랍어 책, Concerning the Hindu Art of Reckoning에 사용된 숫자-표시를 보았기 때문입니다. 알-콰리즈미는 힌두–아라비아 숫자-표시와 방정식 풀이에 대한 방법에 관한 몇 가지 중요한 책을 썼습니다. 알-킨디(Al-Kindi)의 연구와 함께,^{[note 13]} 약 825년에 쓰인 그의 책 On the Calculation with Hindu Numerals은 인도 수학(Indian mathematics)과 인도 숫자-표시(Indian numerals)를 서양에 전파하는 것에 중요한 역할을 했습니다. 알-콰리즈미는 숫자-표시를 아랍어로 주장하지 않았지만, 여러 라틴어 번역을 거쳐, 숫자-표시가 원래 인도인이라는 사실이 사라졌습니다. 단어 알고리듬(algorithm)은 알-콰리즈미의 이름, Algoritmi의 라틴어화에서 파생되고 단어 대수학(algebra) 그의 연구 중 하나의 제목, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (완성과 균형에 의한 계산에 관한 종합 책)에서 파생되었습니다.

이슬람 수학(Islamic mathematics)은 중앙 아시아(Central Asia)인 문명에 알려진 수학을 발전시키고 확장시켰습니다.^[41] 알-콰리즈미는 양의 근을 갖는 이차 방정식의 대수적 해에 대해 철저한 설명을 제공했고,^[42] 알-콰리즈미는 대수학을 초등 형식(elementary form)으로 그 자체로 가르치는 것이었습니다.^[43] 알-콰리즈미는 역시 "감소(reduction)"와 "균형"의 기본 방법을 논의했으며, 빼지는 항을 방정식의 다른 변으로 전치하는 것, 즉, 방정식의 반대 변에서 동류항을 취소하는 것을 참조했습니다. 이것은 알-콰리즈미가 원래 al-jabr로 설명했었던 연산입니다.^[44] 그의 대수학은 역시 더 이상 "해결해야 할 일련의 문제(problem)가 아니라, 조합이 방정식에 대해 모든 가능한 원형을 제공해야 하는 원시 용어로 시작하는 설명(exposition)이며, 이것은 이후 명시적으로 진정한 연구 대상을 구성하는 것"과 관련됩니다. 알-콰리즈미는 역시 그 자체를 위해 및 "문제를 해결하는 과정에서 단순히 나타나는 것이 아니라, 무한한 종류의 문제를 정의하기 위해 특별히 불리는 한 일반적인 방식으로" 방정식을 연구했습니다.^[45]

알 카라지(Al-Karaji)는, 그의 논문 al-Fakhri에서, 미지수 양의 정수 거듭제곱과 정수 근을 통합하기 위한 방법론을 확장합니다.^{[note 14]}^[46] 수학의 역사가(historian) 웨프케(F. Woepcke)는 알-카리지를 "대수(algebra)적 미적분(calculus)의 이론(theory)을 도입했던 최초의 사람"이라고 칭찬했습니다.^[47] 역시 10세기에서, 아불 와파(Abul Wafa)는 디오판토스(Diophantus)의 연구를 아랍어로 번역했습니다. 이븐 알-하이삼(Ibn al-Haytham)은 해석적 기하학(analytic geometry)을 개발했습니다. 알-하이삼은 임의의 정수 거듭제곱의 합에 대해 일반 공식을 결정하기 위해 손쉽게 일반화할 수 있는 방법을 사용하여, 네-번째 거듭제곱의 합에 대해 공식을 유도했습니다. 알-하이삼은 포물면체(paraboloid)의 부피를 찾기 위해 적분을 수행했고, 다항식(polynomial)의 적분에 대한 그의 결과를 사차(foruth degree)까지 일반화할 수 있었습니다.^{[note 15]}^[48] 11세기 후반에, 오마르 하이얌(Omar Khayyam)은 대수적 기하학(algebraic geometry)을 개발했었고, Discussions of the Difficulties in Euclid를 썼고,^{[note 16]} 삼차 방정식(cubic equation)에 대한 일반적인 기하학 해에 대해 썼습니다. 나시르 알-딘 알-투시(Nasir al-din al-Tusi) (Nasireddin)는 구형 삼각법(spherical trigonometry)에서 발전을 만들었습니다. 이 기간 동안 무슬림 수학자들은 아랍 숫자-표시(Arabic numerals)에 십진 점(decimal point) 표기법의 덧셈을 포함했습니다.

전 세계에서 사용되는 현대 아랍 숫자-표시(Arabic numeral) 기호는 10세기에 이슬람 북 아프리카(North Africa)에서 처음 등장했습니다. 동양 아라비아 숫자-표시(Eastern Arabic numerals)의 독특한 서양 아라비아 변형은 전 세계를 통틀어 사용된 현대 아라비아 숫자-표시의 직접적인 조상인 마그레비(Maghreb)와 알 안달루스(Al-Andalus) (때때로 ghubar 숫자-표시라고 불리지만, 그 용어가 항상 허용되지는 않습니다)에서 나타나기 시작했습니다.^[49]

수학에 대한 많은 그리스어와 아랍어 텍스트가 그때에 라틴어로 번역되었으며, 중세 유럽에서 수학의 그 이상의 발전으로 이어졌습니다. 12세기에서, 학자들은 알-콰리즈미의 것과^{[note 17]} 유클리드의 원론(Euclid's Elements)의 전체 텍스트를 포함하여, 과학 아랍어 텍스트를 찾기 위해 스페인과 시칠리아를 여행했습니다.^{[note 18]}^[50]^[51] 숫자-표시를 사용하는 것을 옹호한 유럽 책 중 하나는 피보나치(Fibonacci)로 더 잘 알려진, 피사의 레오나르도에 의한 Liber Abaci였습니다. Liber Abaci는 피보나치가 토끼의 개체에 대한 것을 쓴 수학적 문제로 더 잘 알려져 있습니다. 개체의 성장은 결국 피보나치 수열(Fibonacci sequence)이 되었고, 여기서 항은 앞선 두 항의 합입니다.

Symbolic stage

Symbols by popular introduction date

Early arithmetic and multiplication

기호 대수학으로의 전환은, 여기서 오직 기호가 사용되며, 이븐 알-반나 알-마라쿠시(Ibn al-Banna' al-Marrakushi) (1256–1321)와 아부 알-하산 이븐 알리 알-칼라스사디(Abū al-Hasan ibn Alī al-Qalasādī) (1412–1482)의 연구에서 처음 볼 수 있습니다.^[52]^[53] 알-칼라스사디는 이븐 알-반나에 의해 이전에 마그레비(Maghreb)에서 사용했던 대수적 표기법(algebraic notation)을 개선한 마지막 중세 아랍 대수학자(Arab algebraist)였습니다.^[54] 수학 연산(mathematical operations)을 위한 기호가 부족했던, 이전-연구가 디오판토스(Diophantus)와 브라마굽타(Brahmagupta)의 중략된(syncopated) 표기법과 달리,^[55] 알-칼라스사디의 대수적 표기법은 이들 함수에 대해 기호를 가진 첫 번째였었고 따라서 "대수적 기호주의의 도입을 향한 첫 번째 단계"였습니다. 그는 아라비아 알파벳(Arabic alphabet)에서 문자를 사용하여 수학적 기호(mathematical symbols)를 표현했습니다.^[54]

14세기에는 광범위한 문제를 조사하기 위한 새로운 수학적 개념이 개발되었습니다.^[56] 널리 사용되는 두 가지 산술 기호는 덧셈과 뺄셈, +와 –입니다. 더하기 기호(plus sign)는 니콜 오렘(Nicole Oresme)에^[57]^{[note 19]} 의한 1360년 그의 연구 Algorismus proportionum에서 사용했습니다.^[58] 그것은 "et"에 대해 약어로 생각되며, 앰퍼샌드(ampersand) 기호는 역시 "et"으로 시작하는 것과 거의 같은 방법으로 라틴어에서 "and"를 의미합니다. 파리의 대학(University of Paris)에서 오렘과 이탈리아의 지오바니 디 카살리(Giovanni di Casali)는 상수 가속도를 나타내는 직선 아래 넓이와 이동된 전체 거리를 나타낸다고 주장하면서, 균등하게 가속된 운동을 놓여있는 몸체에 의해 덮여지는 거리의 그래픽 시연을 독립적으로 제공했습니다.^[59] 빼기 기호(minus sign)는 1489년에 요하네스 비트만(Johannes Widmann)에 의해 Mercantile Arithmetic or Behende und hüpsche Rechenung auff allen Kauffmanschafft에서 사용되었습니다.^[60] 비트만은 빼기 기호를 더하기 기호와 함께 사용하여, 각각 부족와 초과를 나타내는 것입니다.^[61] Summa de arithmetica, geometria, proportioni e proportionalità에서,^{[note 20]}^[62] 루카 파치올리(Luca Pacioli)는 더하기 및 빼기(plus and minus) 기호에 기호를 사용했었고 대수(algebra)를 포함했습니다.^{[note 21]}

15세기에, 리야스 알-카시(Ghiyath al-Kashi)는 π의 값을 16번째 십진 위치까지 계산했습니다. 카시는 역시 n번째 근을 계산하는 알고리듬을 가지고 있었습니다.^{[note 22]} 1533년에, 레기오몬타누스(Regiomontanus)의 사인과 코사인 테이블이 출판되었습니다.^[63] 스키피오 델 페로(Scipione del Ferro)와 니콜로 폰타나 타르탈리아(Niccolò Fontana Tartaglia)는 삼차 방정식(cubic equation)에 대해 해를 발견했습니다. 제롤라모 카르다노(Gerolamo Cardano)는 그의 학생 로도비코 페라리(Lodovico Ferrari)에 의해 발견된 사차 방정식에 대해 해와 함께, 1545년 그의 책 Ars Magna에서 그것들을 출판했습니다. 제곱근에 대한 제곱근(radical) 기호는^{[note 23]} 크리스토프 후돌프(Christoph Rudolff)에 의해 도입되었습니다.^{[note 24]} 미카엘 스티펠(Michael Stifel)의 중요한 연구 Arithmetica integra는 수학적 표기법에서 중요한 혁신이 포함하고 있습니다.^[64] 1556년에, 니콜로 타르탈리아(Niccolò Tartaglia)는 우선 순위 그룹화에 괄호를 사용했습니다. 1557년에, 로버트 레코드(Robert Recorde)는 영국 독자를 위해 등호(=)와 마찬가지로 더하기 및 빼기 기호를 도입했던 The Whetstone of Witte을 출판했습니다. 1564년에, 제롤라모 카르다노(Gerolamo Cardano)는 확률 이론(probability theory)의 초기 단계를 시작하는 우연의 게임(games of chance)을 분석했습니다. 1572년에, 라파엘 봄벨리(Rafael Bombelli)는 삼차 방정식을 풀기 위한 카르다노의 공식에 나타날 수 있는 허수 양(imaginary quantities)을 처리하는 방법을 보여주는 그의 L'Algebra를 출판했습니다. 1585년 네덜란드어로 출판된, [[Simon Stevin|시몬 스테빈(Simon Stevin)]의 책 De Thiende ('십분의 일의 기술')은 나중에 실수 시스템(real number system)에 대한 모든 연구에 영향을 미쳤던 십진 표기법(decimal notation)의 시스템적인 처리를 포함하고 있습니다. 프랑수아 비에트(François Viète)의 New algebra (1591)는 대수적 표현의 현대적인 표기법 조작을 도입했습니다. 넓은 지역의 탐색과 정확한 지도를 위해, 삼각법(trigonometry)은 수학의 주요 가지로 성장했습니다. 바르톨로마이오스 피티스쿠스(Bartholomaeus Pitiscus)는 1595년 그의 Trigonometria를 출판하면서 "삼각법"이라는 단어를 만들었습니다.

존 네이피어(John Napier)는 로그(logarithms)의 발명가로 가장 잘 알려져 있고^{[note 25]}^[65] 산술과 수학에서 십진 점(decimal point)의 사용을 공통으로 만들었습니다.^[66]^[67] 네이피어 후에, 에드먼드 건터(Edmund Gunter)가 미끄럼 자(slide rules)의 기반이 되는 로그 스케일(logarithmic scale) (직선, 또는 자)을 만들었으며, 직접 곱셈(multiplication)과 나눗셈(division)을 수행하기 위해 하나의 또 다른 것에 의해 둘의 그러한 스케일 슬라이딩을 사용했던 윌리엄 오트레드(William Oughtred)였습니다; 그리고 그는 1622년에 미끄럼 자의 발명가로 알려져 있습니다. 1631년에 오트레드는 곱셈 기호(×) 그의 비례 기호,^{[note 26]} 및 사인(sine)과 코사인(cosine) 함수에 대해 약어 sin과 cos을 도입했습니다.^[68] 알버트 지라드(Albert Girard)는 역시 그의 논문에서 삼각 함수(trigonometric functions)에 대해 약어 'sin', 'cos', 및 'tan'을 사용했습니다.

요하네스 케플러(Johannes Kepler)는 무한소(infinitesimals)의 수학적 응용의 개척자 중 한 명입니다.^{[note 27]} 르네 데카르트(René Descartes)는 무한소 미적분학(infinitesimal calculus)과 해석학(analysis)의 발견에 결정적인 대수학과 기하학 사이의 다리, 해석적 기하학(analytical geometry)의 아버지로 공인됩니다.^{[note 28]} 17세기에, 데카르트는 해석적 기하학의 발전을 가능하게 했던 데카르트 좌표(Cartesian co-ordinates)를 도입했습니다.^{[note 29]} 블레즈 파스칼(Blaise Pascal)은 평생 동안 수학에 영향을 미쳤습니다. 1653년의 그의 Traité du triangle arithmétique ("산술 삼각형에 대한 논문")에서는 이항 계수(binomial coefficient)에 대해 편리한 테이블-형식의 표현을 설명했습니다.^{[note 30]} 피에르 드 페르마(Pierre de Fermat)와 블레즈 파스칼은 확률(probability)을 조사했을 것입니다.^{[note 31]} 존 월리스(John Wallis)는 무한대 기호(infinity symbol)를 도입했습니다.^{[note 32]} 그는 이 표기법을 무한소에 대해 유사하게 사용했습니다.^{[note 33]} 1657년에, 크리스티안 하위헌스(Christiaan Huygens)는 확률에 관한 논문, On Reasoning in Games of Chance를 출판했습니다.^{[note 34]}^[69]

요한 한(Johann Rahn)은 1659년에 나눗셈 기호(division sign) (÷, 용도-변경된 오벨루스(obelus) 변형)와 그러므로 기호(therefore sign)를 도입했습니다. 윌리엄 존스(William Jones)는 1706년 Synopsis palmariorum mathesios에서 π를 사용했는데,^[70] 왜냐하면 그것이 그리스 단어 perimetron (περιμετρον)의 첫 글자이기 때문이며, 그것은 그리스어로 둘레(perimeter)를 의미합니다. 이 사용법은 오일러에 의해 1737년에 대중화되었습니다. 1734년에, 피에르 부거(Pierre Bouguer)는 부등식 기호(inequality sign) 아래에 이중 수평 막대를 사용했습니다.^[71]

Derivatives notation: Leibniz and Newton

Derivative notations
Sir Isaac Newton Gottfried Wilhelm Leibniz

선형 대수(linear algebra)의 연구는 선형 방정식(linear equation)의 시스템을 풀기 위해 사용되었던 행렬식(determinant)의 연구에서 나타났습니다. 미적분학은 각각 작성자 중 한 명이 만든 두 가지 주요 표기법 시스템을 가졌습니다: 하나는 아이작 뉴턴(Isaac Newton)에 의해 개발되었고 다른 하나는 고트프리트 라이프니츠(Gottfried Leibniz)에 의해 개발되었습니다. 라이프니츠의 표기법은 오늘날 가장 자주 사용되는 표기법입니다. 뉴턴의 표기법은 단순히 함수 위에 배치된 점 또는 대시였습니다.^{[note 35]} 현대적인 사용법에서, 이 표기법은 일반적으로 시간에 관한 물리량의 도함수를 나타내고, 역학(mechanics)의 과학에서 자주 사용됩니다. 라이프니츠는, 다른 한편으로, 미분을 나타내기 위해 접두사로 문자 d를 사용했었고, 도함수를 나타내는 표기법을 마치 특수한 유형의 분수인 것처럼 도입했습니다.^{[note 36]} 이 표기법은 함수의 도함수가 취해지는 것에 관한 변수를 명백하게 만듭니다. 라이프니츠는 역시 적분 기호를 만들었습니다.^{[note 37]} 그 기호는 "합"을 의미하는 라틴어(Latin) 단어 Summa를 나타내는 길쭉한 S입니다. 곡선 아래 넓이를 찾을 때, 적분은 종종 넓이를 그것의 넓이가 더해지는 무한하게 많은 길고, 얇은 직사각형으로 나눔으로써 묘사됩니다. 따라서, 적분 기호는 합에 대해 길쭉한 s입니다.

High division operators and functions

이 시대의 알파벳 문자(letters of the alphabe)t는 수량(quantity)의 기호로 사용되었습니다; 그리고 비록 문자 선택에 관한 많은 다양성이 존재했지만, 다음 역사에서 보편적으로 인식되는 몇 가지 규칙이 있었습니다.^[24] 여기서 따라서 방정식의 역사에서 알파벳의 첫 문자가 암시적으로 계수(coefficients)로 알려졌으며, 마지막 문자는 미지수 항(unknown term) (incerti ordinis)으로 알려졌습니다. 대수적 기하학(algebraic geometry)에서, 다시, 유사한 규칙이 관찰되어야 했으며, 알파벳의 마지막 문자는 그곳에서 변수 또는 현재 좌표(coordinates)를 나타냅니다. $\pi$ , $e$ , 등과 같은 특정 문자는 보편적인 동의(universal consent)에 의해 자주 발생하는 숫자 3.14159 ..., 및 2.7182818 ....,^{[note 38]} 등의 기호로 사용되었고, 임의의 다른 승인에 그것들의 사용은 가능한 한 피해야 했습니다.^[24] 문자는, 역시, 연산의 기호로 사용되어야 했었고, 앞서 언급한 다른 임의의 연산 문자와 함께 사용되었습니다. 문자 $d$ , 길쭉한 $S$ 는 미분 미적분과 적분 미적학에서 연산 기호로, $\Delta$ 와 Σ는 차이의 미적분에서 사용되었습니다.^[24] 함수형 표기법(functional notation)에서, 연산의 기호로 문자는 수량(quantity)의 기호로 고려되는 또 다른 문자와 결합됩니다.^[24]^{[note 39]}

1718년 시작에서, 토마스 트위닌(Thomas Twinin)은 나눗셈 슬래시(division slash) (사선(solidus))를 사용했으며, 초기 아랍어 수평 분수 막대(horizontal fraction bar)에서 파생했습니다. 피에르-시몽, 드 라플라스 후작(Pierre-Simon, marquis de Laplace)은 널리 사용되는 라플라스 미분 연산자를 개발했습니다.^{[note 40]} 1750년에, 게브리엘 크라메르(Gabriel Cramer)]는 선형 시스템을 풀기 위해 "클라메르의 규칙"을 개발했습니다.

Euler and prime notations

Leonhard Euler's signature

레온하르트 오일러(Leonhard Euler)는 역사상 가장 다작의 수학자 중 한 명이고, 정식 표기법의 다작의 발명가이기도 했습니다. 그의 공헌은 자연 로그(natural logarithm)의 밑수를 나타내기 위해 e의 그의 사용을 포함합니다. $e$ 가 선택된 이유는 정확히 알려져 있지 않지만, 아마도 알파벳의 네 글자가 이미 변수와 기타 상수를 나타내기 위해 공통적으로 사용되었기 때문일 것입니다. 오일러는 일관되게 파이(pi)를 나타내기 위해 $\pi$ 를 사용했습니다. $\pi$ 의 사용은 윌리엄 존스(William Jones)에 의해 $\pi$ 를 제안되었으며, 그는 그것을 둘레(perimeter)의 속기로 사용했으며, 오일러는 음수 일의 제곱근을 나타내기 위해 $i$ 를 사용했지만,^{[note 41]} 그는 이전에 그것을 무한 숫자로 사용했습니다.^{[note 42]}^{[note 43]} 합계(summation)에 대해, 오일러는 시그마(sigma), Σ를 사용했습니다.^{[note 44]} 함수(functions)에 대해, 오일러는 표기법 $f(x)$ 를 $x$ 의 함수를 나타내기 위해 사용했습니다. 1730년에, 오일러는 감마 함수(gamma function)를 썼습니다.^{[note 45]} 1736년에, 오일러는 그래프 이론 연구를 시작하는 쾨니히스베르크의 일곱 다리(Seven Bridges of Königsberg)에 대한 그의 논문을 썼습니다.^[72]

수학자 윌리엄 에머슨(William Emerson)은^[73] [[비례성 기호(proportionality sign)를 개발했을 것입니다.^{[note 46]}^{[note 47]}^[74]^[75] 훨씬 나중에 다양한 비례적 현상의 값의 추상적 표현에서, 부분-당 표기법(parts-per notation)이 기타 무차원 수량(dimensionless quantities)의 작은 값을 설명하기 위해 유사 단위의 집합으로 유용하게 되었을 것입니다. 드 콩도르세 후작(Marquis de Condorcet)은, 1768년에, 부분 미분(partial differential) 기호를 발전시켰습니다.^{[note 48]} 1771년에, 알렉상드르-테오필 방데르몽드(Alexandre-Théophile Vandermonde)는 위치의 기하학과 관련된 매듭의 속성(properties of knots)을 논의할 때 토폴로지적 특질의 중요성을 추론했습니다. 1772년과 1788년 사이에, 조제프-루이 라그랑주(Joseph-Louis Lagrange)는 라그랑주 역학(Lagrangian mechanics)이라고 불리는 고전 "뉴턴" 역학의 공식과 계산을 다시 공식화했습니다. 도함수의 프라임 기호(prime symbol)는 역시 라그랑주에 의해 만들어졌습니다.

“

그러나 우리의 의견으로는 이러한 종류의 진리는 표기법이 아니라 개념에서 도출되어야 합니다.

”

— Carl Friedrich Gauss^{[note 49]}

Gauss, Hamilton, and Matrix notations

19세기로 접어들면서, 카를 프리드리히 가우스(Carl Friedrich Gauss)는 합동 관계(congruence relation)에 대해 항등 기호(identity sign)를 개발했었고, 이차 상호관계(Quadratic reciprocity)에서, 정수 부분(integral part)을 개발했습니다. 가우스는 기하학(geometry)에서, 복소 변수(complex variable)의 함수(functions)와 급수(series)의 수렴에 기여했습니다. 그는 대수학의 기본 정리(fundamental theorem of algebra)와 이차 상호 법칙(quadratic reciprocity law)의 만족스러운 증명을 제시했습니다. 가우스는 초기에 측지학(geodesy)에서 발전으로 나열된 가우스 소거법(Gaussian elimination)을 사용함으로써 선형 시스템을 푸는 이론을 개발했습니다.^[76] 그는 역시 곱 기호(product sign)를 개발했을 것입니다. 역시 이 시기에, 닐스 헨리크 아벨(Niels Henrik Abel)과 에바리스트 갈루아(Évariste Galois)는 그룹 이론(group theory)과 필드 이론(field theory)을 연결하여 방정식의 해결가능성(solvability of equations)에 대한 연구를 수행했습니다.^{[note 50]}

1800년대 이후, 크리스티앙 크랑(Christian Kramp)는 비-정수에 적용되는 일반화된 팩토리얼 함수에서 그의 연구 동안 팩토리얼(factorial) 표기법을 장려했을 것입니다.^[77] 조셉 디아즈 게르곤(Joseph Diaz Gergonne)은 집합 포함(set inclusion) 기호를 도입했습니다.^{[note 51]} 페터 구스타프 르죈 디리클레(Peter Gustav Lejeune Dirichlet)은 산술 진행에 대한 디리클레의 정리(Dirichlet's theorem on arithmetic progressions)의 증명을 제공하기 위해 디리클레 L-함수(Dirichlet L-functions)를 개발했었고 해석적 숫자 이론(analytic number theory)을 시작했었습니다.^{[note 52]} 1828년에, 가우스는 테오레마 에그레기움(Theorema Egregium (라틴어에서 놀랄만한 정리)를 입증했으며, 표면의 속성을 설정합니다. 1830년대에, 조지 그린(George Green)은 그린의 함수(Green's function)를 개발했습니다. 1829년에, 카를 구스타프 야코프 야코비(Carl Gustav Jacob Jacobi)는 그의 타원형(elliptic) 세타 함수(theta function)를 갖는 Fundamenta nova theoriae functionum ellipticarum을 출판합니다. 1841년까지, 카를 바이어슈트라스(Karl Weierstrass), "현대 해석학(analysis)의 아버지"는 행렬의 행렬식(determinant of a matrix)과 절댓값(absolute value)의 개념에 대해 정교하게 만들었습니다.

행렬 표기법(Matrix notation)은 아서 케일리(Arthur Cayley)에 의해 라그랑주의 Mécanique analytique와 라플라스의 일부 연구를 읽음으로써 제안되어 왔던 주제에 대한 그의 세 개의 논문에서 더 완전히 개발했을 것입니다.^[78] 케일리는 행렬 곱셈(matrix multiplication)과 행렬 역(matrix inverse)을 정의했습니다. 케일리는 행렬을 나타내기 위해 단일 문자를 사용했었고,^[79] 따라서 행렬을 집합적인 대상으로 취급했습니다. 그는 역시 행렬과 행렬식 사이의 연결을 깨닫았고,^[80] "There would be many things to say about this theory of matrices which should, it seems to me, precede the theory of determinants"라고 썼습니다.^[81]

“

[... 수학적 쿼터니언은] 넷의 차원을 가지거나, 적어도 넷의 차원에 대한 참조를 포함합니다.

”

— William Rowan Hamilton^{[note 53]}

윌리엄 로언 해밀턴(William Rowan Hamilton)은 벡터 미분(vector differential)에 대해 나블라 기호(nabla symbol)를^{[note 54]} 도입했을 것입니다.^[82]^[83] 이것은 이전에 해밀턴에 의해 일반적인-목적 연산자 기호(operator sign)로 사용했습니다.^[84] 해밀턴은 지금 해밀턴 역학(Hamiltonian mechanics)이라고 불리는 뉴턴 역학(Newtonian mechanics)을 재구성했습니다. 이 연구는 전자기학(electromagnetism)과 같은 고전적 필드 이론의 현대적 연구에 대한 핵심으로 입증되어 왔습니다. 이것은 역시 양자 역학(quantum mechanics)의 발전에 중요했었습니다.^{[note 55]} 수학에서, 그는 아마도 쿼터니언 표기법(quaternion notation)과 이중-쿼터니언(biquaternion)의 발명가로 가장 잘 알려져 있을 것입니다.^{[note 56]} 해밀턴은 역시 1846년에 "텐서(tensor)"라는 단어를 도입했습니다.^[85]^{[note 57]} 제임스 코클(James Cockle)은 테사린(tessarine)과^{[note 58]} 1849년에, 코쿼터니언(coquaternions)를 개발했습니다. 1848년에, 제임스 조지프 실베스터(James Joseph Sylvester)는 행렬 대수학(matrix algebra)에 행렬(matrix)이라는 용어를 도입했습니다.^{[note 59]}

Maxwell, Clifford, and Ricci notations

1864년에, 제임스 클러크 맥스웰(James Clerk Maxwell)은 전자기장의 당시의 모든 지식을 A Dynamical Theory of the Electromagnetic Field에 포함된 20 변수의 20 방정식을 갖는 연결된 미분 방정식(differential equation)의 집합으로 축소했습니다.^[87] (맥스웰의 방정식(Maxwell's equations)을 참조하십시오.) 사용하기에 필요한 계산의 방법은 라그랑주에 의해 제공되었고, 이후에는 약간의 수정을 거쳐 해밀턴의 방정식(Hamilton's equations)에 의해 개발되었습니다. 그것은 보통 해밀턴의 원리(Hamilton's principle)로 참조됩니다; 원래 형식에서 그 방정식이 사용될 때, 그것들은 라그랑주의 방정식(Lagrange's equations)으로 알려져 있습니다. 1871년에, 리처드 데데킨트(Richard Dedekind)는 넷의 산술 연산 아래에 닫혀 있는 실수 또는 복소수의 집합을 필드(field)라고 불렀습니다. 1873년에, 맥스웰은 A Treatise on Electricity and Magnetism을 발표했습니다.

1878년에, 윌리엄 킹던 클리퍼드(William Kingdon Clifford)는 그의 Elements of Dynamic를 출판했습니다.^[88] 클리터드는 분할-이중쿼터니언(split-biquaternions)을 개발했으며,^{[note 60]} 그는 algebraic motors라고 불렀습니다. 클리퍼드는 완전한 쿼터니언 표기법에서 두 벡터의 점 곱(dot product)과 교차 곱(cross product)을 분리함으로써 쿼터니언 연구를 제거했습니다.^{[note 61]} 이 접근 방식은 벡터 미적분학(vector calculus)을 삼 차원(three dimensions)에서 연구하는 엔지니어와 다른 사람들에게 유용하게 만들고 네 번째 차원(fourth dimension)의 선행–지연 효과(lead–lag effect)를 회의적(skeptical)으로^{[note 62]} 만들었습니다.^{[note 63]} 공통 벡터 표기법(vector notation)은 공간적(spatial)이거나 벡터 공간(vector space)의 더 추상적인 구성원인 벡터로 연구할 때 사용되고, 반면에 각도 표기법(angle notation) (또는 페이저(phasor) 표기법)은 전자공학(electronics)에서 사용되는 표기법입니다.

1881년에, 레오폴드 크로네커(Leopold Kronecker)는 그가 "유리성의 도메인"이라고 불렀던 것을 정의했으며, 이것은 현대적인 용어에서 유리수의 필드(field of rational numbers)의 필드 확장(field extension)입니다.^[89] 1882년에, 후세인 테브픽 파샤(Hüseyin Tevfik Paşa)는 "Linear Algebra"라는 제목의 책을 저술했습니다.^[90]^[91] 켈빈 경(Lord Kelvin)의 에테르(aetheric) 원자 이론(atom theory) (1860년대)은, 1885년에, 피터 거스리 타이트(Peter Guthrie Tait)에게 타이트 추측(Tait conjectures)으로 알려진 최대 10개의 교차점을 갖는 토폴로지적(topological) 매듭의 테이블을 발표하는 것으로 이어졌습니다. 1893년에, 하인리히 마르틴 베버(Heinrich Martin Weber)는 추상적인 필드(abstract field)의 명확한 정의를 제공했습니다.^{[note 64]} 텐서 미적분(Tensor calculus)은 1887년과 1896년 사이에 그레고리오 리치-쿠르바스트로(Gregorio Ricci-Curbastro)에 의해 개발되었으며, 1892년에 absolute differential calculus이라는 제목으로 발표되었고,^[92] 현대 "텐서"의 사용법은 1898년에 볼데마 포크트(Woldemar Voigt)에 의해 언급되었습니다.^[93] 1895년에, 앙리 푸앵카레(Henri Poincaré)는 Analysis Situs를 출판했습니다.^[94] 1897년에, 찰스 프로테우스 스타인메츠(Charles Proteus Steinmetz)는 Ernst J. Berg의 도움과 함께, Theory and Calculation of Alternating Current Phenomena를 출판했습니다.^[95]

From formula mathematics to tensors

“

위의 제안은 때때로 유용합니다.

”

— Bertrand Russell

^{[note 65]}

1895년에, 주세페 페아노(Giuseppe Peano)는 그의 Formulario mathematico를 발행했으며,^[96] 수학을 특수 기호를 기반으로 한 간결한 텍스트로 소화하기 위한 노력을 기울였습니다. 그는 벡터 공간(vector space)과 선형 맵(linear map)의 정의를 제공했을 것입니다. 그는 역시 교집합 기호(intersection sign), 합집합 기호(union sign), 구성원 기호(membership sign) (...의 원소), 및 존재 한정어(existential quantifier) (...존재합니다)를 도입했을 것입니다.^{[note 66]} 페아노는 1900년에 파리 회의에서 버트런드 러셀(Bertrand Russell)에게 그의 연구를 전달했을 것입니다; 그것은 러셀에게 깊은 인상을 주었고 러셀 역시 수학을 더 간결하게 표현하려는 충동에 사로잡혔습니다. 그 결과는 알프레드 노스 화이트헤드(Alfred North Whitehead)와 함께 쓰인 Principia Mathematica였습니다. 이 논문은 기호가 지배적이었던 현대 문학에서 분수령을 표시합니다.^{[note 67]} 리치-쿠르바스트로(Ricci-Curbastro)와 툴리오 레비-치비타(Tullio Levi-Civita)는 1900년경 텐서 인덱스 표기법(tensor index notation)을 대중화했습니다.^[97]

Mathematical logic and abstraction

Abstraction
Felix Klein Georg Cantor

이 기간이 시작에서, 펠릭스 클라인(Felix Klein)의 "Erlangen program"은 다양한 기하학의 놓여있는 주제를 식별했었으며, 그것들의 각각을 주어진 대칭(symmetries)의 그룹 아래에서 불변 속성(properties invariant)의 연구로 정의했습니다. 이 추상화의 수준은 기하학과 추상 대수학(abstract algebra) 사이의 연결을 드러냈습니다. 게오르크 칸토어(Georg Cantor)는^{[note 68]} 초월유한 집합의 세는 숫자(cardinal number)에 대해 알레프 기호(aleph symbol)를 도입했을 것입니다.^{[note 69]} 세는 숫자에 대해 그의 표기법은 자연수 아래첨자를 갖는 히브리 문자 $\aleph$ (알레프)였습니다; 순서 숫자에 대래 그는 그리스 문자 ω (오메가)를 사용했습니다. 이 표기법은 언어에 의미를 부여하는 일부 체계에 따라 순서 숫자(ordinal number)를 이름짓는 유한 알파벳에서 기호의 유한 수열의 순서-숫자 표기법(ordinal notation)에서 오늘날에도 여전히 사용되고 있습니다. 그의 이론은 많은 논쟁을 불러일으켰습니다. 칸토어는, 푸리에 급수(Fourier series)의 그의 연구에서, 유클리드 공간(Euclidean space)에서 점 집합을 고려했을 것입니다.

20세기로 전환한 후, 조사이어 윌러드 깁스(Josiah Willard Gibbs)는 물리적 화학(physical chemistry)에서 점 곱(dot product)에 대해 중간 점(middle dot)을, 교차 곱(cross product)에 대해 곱셈 기호(multiplication sign)를 도입했을 것입니다. 그는 역시 Vector Analysis에서 도입되었던 스칼라와 벡터 곱에 대해 표기법을 제공했을 것입니다. 1904년에, 에른스트 체르멜로(Ernst Zermelo)는 선택의 공리(axiom of choice)와 바른-순서화 정리(well-ordering theorem)의 증명을 촉진합니다.^[98] 버트런드 러셀(Bertrand Russell)은 1906년에 논리적 논리합(logical disjunction) (OR)를 도입했을 것입니다. 역시 1906년에, 푸앵카레는 On On the Dynamics of the Electron을 출판했었고^[99] 모리스 프레셰(Maurice Fréchet)는 메트릭 공간(metric space)을 소개했을 것입니다.^[100] 나중에, 게르하르트 코발레프스키(Gerhard Kowalewski)와 커스버트 에드먼드 컬리스(Cuthbert Edmund Cullis)는^[101]^[102]^[103] 각각 행렬 표기법, 괄호 안의 행렬, 및 상자 행렬 표기법을 차례로 도입했을 것입니다. 1907년 이후, 수학자는^{[note 70]} 매듭 그룹(knot group)의 관점에서 매듭을 연구하고 호모토피 이론(homology theory)에서 불변을 연구했습니다.^{[note 71]} 1908년에, 조지프 웨더번(Joseph Wedderburn)의 구조 정리는 필드에 걸쳐 유한-차원 대수학에 대해 공식화되었습니다. 역시 1908년에, 에른스트 체르멜로(Ernst Zermelo)는 "확정(definite)" 속성과 최초의 공리적 집합 이론(axiomatic set theory), 체르멜로 집합 이론(Zermelo set theory)을 제안했습니다. 1910년에, 에른스트 슈타이니츠(Ernst Steinitz)는 영향력 있는 논문 Algebraic Theory of Fields를 출판했습니다.^{[note 72]}^{[note 73]} 1911년에, 스타인메츠(Steinmetz)는 Theory and Calculation of Transient Electric Phenomena and Oscillations를 출판했습니다.

알베르트 아인슈타인(Albert Einstein)은, 1916년에, 아인슈타인 표기법(Einstein notation)을 도입했으며,^{[note 74]} 이것은 공식에서 인덱스된 항(indexed terms)의 집합에 걸쳐 합해지고, 따라서 표기법의 간결함을 발휘했습니다. 아놀드 솜머펠트(Arnold Sommerfeld)는 1917년에 윤곽 적분(contour integral) 기호를 만들었을 것입니다. 역시 1917년에, 드리트리 미리마노프(Dimitry Mirimanoff)는 규칙성의 공리(axiom of regularity)를 제안합니다. 1919년에, 테오도어 칼루차(Theodor Kaluza)는 오-차원(five dimensions)을 사용하여 일반 상대성(general relativity) 방정식을 풀었을 것이고, 그 결과는 전자기 방정식을 나타났을 것입니다.^[104] 이것은 1921년에 "Zum Unitätsproblem der Physik"에 출판되었을 것입니다.^[105] 1922년에, 아브라함 프렝켈(Abraham Fraenkel)과 토랄프 스콜렘(Thoralf Skolem)은 사양의 공리 스키마(axiom schema of specification)를 대체의 공리 스키마(axiom schema of replacement)으로 대체하는 것을 독립적으로 제안했습니다. 역시 1922년에, 체르멜로–프렝켈 집합 이론(Zermelo–Fraenkel set theory)이 개발되었습니다. 1923년에, 스타인메츠(Steinmetz)는 Four Lectures on Relativity and Space를 출판했을 것입니다. 1924년 즈음, 얀 아르놀뒤스 스하우턴(Jan Arnoldus Schouten)은 20세기 초에 일반 상대성(general relativity)과 미분 기하학(differential geometry)에 절대 미분 미적분을 적용하는 동안 리치 계산법(Ricci calculus) 프레임워크에 대해 현대 표기법과 형식주의를 개발했을 것입니다.^{[note 75]}^[106]^[107]^[108] 1925년에, 엔리코 페르미(Enrico Fermi)는 파울리(Pauli) 제외 원리를 따르는 많은 동일한 입자로 구성하는 시스템을 기술했을 것이며, 그 후 확산 방정식(diffusion equation) (페르미 나이 방정식(Fermi age equation))을 개발합니다. 1926년에, 오스카르 클라인(Oskar Klein)은 칼루차–클라인 이론(Kaluza–Klein theory)을 개발했을 것입니다. 1928년에, 에밀 아르틴(Emil Artin)은 아르틴 링(Artinian ring)을 갖는 링 이론(ring theory)을 추상화했습니다. 1933년에, 안드레이 콜모고로프(Andrey Kolmogorov)는 Kolmogorov axioms를 소개합니다. 1937년에, 브루노 데 피네티(Bruno de Finetti)는 ""연작적 주관적(operational subjective)" 개념(concept)을 추론했습니다.

Mathematical symbolism

수학적 추상화는 수학적 개념의 놓여있는 본질(essence)을 추출하고,^[109]^[110] 원래 연결되었을 수 있는 실제 세계 대상에 대한 임의의 종속성을 제거하고,^[111] 그것이 더 넓은 응용을 가지거나 동등한 현상(phenomena)의 다른 추상적 설명 사이의 일치하도록 그것을 일반화함으로써 시작되었습니다. 현대 수학의 둘의 추상적 영역은 카테고리 이론(category theory)과 모델 이론(model theory)입니다. 버트런드 러셀(Bertrand Russell)은,^[112] "일상 생활의 단어는 충분히 추상적이지 않기 때문에 보통의 언어는 물리학이 실제로 주장하는 것을 표현하는 데 완전하게 부적합합니다. 오직 수학과 수학적 논리가 물리학자가 말하려는 만큼 적게 말할 수 있습니다"라고 말했습니다. 그러나, 우리가 현실 세계의 대상을 수학으로 대체할 수 있고, 방정식을 따라 방정식을 헤매고, 현실성과 관련을 가지지 않는 개념 구조를 구축할 수 있습니다.^[113]

기호적 논리(symbolic logic)는 기호의 문자열의 순수하게 형식적 속성을 연구합니다. 이 분야에서 관심은 두 가지 출처에서 비롯됩니다. 첫째, 기호적 논리에서 사용되는 표기법은 철학적 논리(philosophical logic)에서 사용되는 단어를 나타내는 것으로 보일 수 있습니다. 둘째, 기호적 논리에서 발견되는 기호를 조작하는 것에 대해 규칙은 컴퓨팅 기계(computing machine)에서 구현될 수 있습니다. 기호적 논리는 보통 둘의 부분필드, 명제 논리(propositional logic)와 술어 논리(predicate logic)로 나뉩니다. 다른 관심의 논리는 시간 논리(temporal logic), [[modal logic|양상 논리(modal logic), 및 퍼지 논리(fuzzy logic)를 포함합니다. 명제 논리(propositional logic)라고 불리는 기호적 논리학의 분야는 역시 propositional calculus이라고 불리며, 상수(constants)와 논리 연산자(logical operator)로 형성된 문장의 속성을 연구합니다.^{[note 76]} 해당하는 논리적 연산은 각각 논리곱(conjunction), 논리합(disjunction), 물질 조건부(material conditional), 쌍-조건부(biconditional), 및 부정(negation)으로 알려져 있습니다. 이들 연산자는 키워드(keywords)와 기호적 표기법에 의해 표시됩니다.^{[note 77]}

이 시기 동안 도입된 수학적 논리 표기법 중 일부는 부울 대수(Boolean algebra)에 사용된 기호 집합을 포함했습니다. 이것은 1854년에 조지 부울(George Boole)에 의해 만들어졌습니다. 부울 자신은 논리를 수학의 한 가지로 보지 않았지만, 그것은 어쨌든 포함되도록 되었습니다. 부울 대수에서 찾아지는 기호는 $\land$ (AND), $\lor$ (OR), 및 $\lnot$ (not)를 포함합니다. 이들 기호와 다른 진리값(truth value)을 나타내기 위한 문자와 함께, 우리는 $a\lor \lnot a=1$ , 즉 "(a는 참임 OR a는 참이 아님)은 참임"과 같은 논리적 명제를 만들 수 있으며, 그것은 a가 참이거나 참이 아님 (즉, 거짓) 중 하나라는 것이 참임을 의미합니다. 부울 대수는 그 자체로 많은 실용적인 용도를 가지고 있지만, 논리학에서 사용되는 많은 기호 집합의 시작이기도 합니다.^{[note 78]} 원래 술어 미적분학이라고 불리웠던 술어 논리는 변수(variables)의 도입에 의해,^{[note 79]} 및 술어(predicates)라고 불리는 변수를 포함하는 문장에 의해 명제 논리를 확장합니다.^{[note 80]} 게다가, 술어 논리는 한정어(quantifiers)를 허용합니다.^{[note 81]} 이들 논리 기호(logic symbol)와 술어 논리에서 추가적인 한정어(quantifier)와 함께,^{[note 82]} 유효한(valid) 증명(proofs)이 비합리적으로 인공적이지만,^{[note 83]} 구문론적인 것으로 만들어질 수 있습니다.^{[note 84]}

Gödel incompleteness notation

“

v Gen r도 아니고 Neg (v Gen r)도 아닌 것이 Flg (κ)에 속함을 만족하는 ω-일관된 재귀 클래스 κ 공식의 모든 각 재귀 클래스 기호 r에 해당합니다.

”

— Kurt Gödel^[114]

그의 불완전성 정리(incompleteness theorems)를 증명하는 동안,^{[note 85]} 쿠르트 괴델(Kurt Gödel)은 논리학에서 통상적으로 사용되는 기호에 대한 대안을 만들었습니다. 그는 집합 숫자로 연산을 나타내는 숫자였던 괴델 숫자(Gödel number)와 10보다 큰 소수를 갖는 변수를 사용했습니다. 괴델 숫자와 함께, 논리적 명제는 수열로 분리될 수 있습니다. 괴델은 그런-다음 한 단계 더 나아가, n 소수를 취하고, 수열에 있는 숫자의 거듭제곱에 그것을 넣습니다. 이들 숫자는 그런-다음 함께 곱하여 최종 곱을 얻고, 모든 각 논리 명제에 자체의 숫자를 부여합니다.^[115]^{[note 86]}

Contemporary notation and topics

Early 20th-century notation

표기법의 추상화는 지속적인 과정이고 많은 수학적 주제의 역사적 발전은 구체적인 것에서 추상적인 것으로의 진행을 보여줍니다. 다양한 집합 표기법(set notation)이 기본적인 대상 집합(sets)에 대해 개발될 것입니다. 1924년경, 다비트 힐베르트(David Hilbert)와 리하르트 쿠란트(Richard Courant)는 ""수학적 물리학의 방법. 편미분 방정식"을 발표했습니다.^[116] 1926년에, 오스카르 클라인(Oskar Klein)과 발터 고르돈(Walter Gordon)은 상대론적 입자를 설명하기 위해 클라인–고르돈 방정식(Klein–Gordon equation)을 제안했습니다.^{[note 87]} 복사와 물질 상호작용을 설명하는 양자 이론(quantum theory)의 첫 공식화는 1920년 동안 처음으로 원자(atom)의 자발적 방출의 계수를 계산할 수 있었던 폴 에이드리언 모리스 디랙(Paul Adrien Maurice Dirac)에 기인합니다.^[117] 1928년에, 상대론적(relativistic) 디랙 방정식(Dirac equation)은 상대론적으로 움직이는 전자(electron)의 행동을 설명하기 위해 디랙에 의해 공식화되었습니다.^{[note 88]} 디랙은 입자의 생성과 소멸 연산자의 개념의 도입과 함께 조화 진동자(harmonic oscillator)의 앙상블로 전자기 필드의 정량화를 설명했습니다. 입자의. 그 다음 해에, 볼프강 파울리(Wolfgang Pauli), 유진 위그너(Eugene Wigner), 파스쿠알 요르단(Pascual Jordan), 및 베르너 하이젠베르크(Werner Heisenberg)의 공헌과 함께, 엔리코 페르미(Enrico Fermi)에 의한 양자 전기역학의 우아한 공식화로,^[118] 물리학자들은 원칙적으로 광자와 하전 입자를 포함하는 임의의 물리적 과정에 대해 임의의 계산을 수행하는 것이 가능하다고 믿게 되었습니다.

1931년에, 알렉산드루 프로카(Alexandru Proca)는 핵의 힘(nuclear force)의 벡터 중간자(meson) 이론과 상대론적 양자 필드 방정식(relativistic quantum field equations)에 대해 프로카 방정식(Proca equation) (오일러–라그랑주 방정식)을 개발했습니다.^{[note 89]} 1937년에 존 아치볼드 휠러(John Archibald Wheeler)는 S-행렬(S-matrix)을 개발합니다. 아놀드 노드시키(Arnold Nordsieck),^[119] 및 빅토어 바이스코프(Victor Weisskopf)와^[120] 함께 1937년과 1939년에 펠릭스 블로흐(Felix Bloch)에 의한 연구는 그러한 계산이 로버트 오펜하이머(Robert Oppenheimer)에 의해 이미 지적된 문제, 섭동 이론(perturbation theory)의 오직 일-차에서 신뢰할 수 있는 것으로 드러났습니다.^[121] 급수에서 더 높은 차수에서 무한대가 나타났고, 그러한 계산을 무의미하게 만들고 이론 자체의 내부 일관성에 심각한 의심을 던졌습니다. 당시에 이 문제에 대해 해결책이 알려지지 않았기 때문에, 특수 상대성(special relativity)과 양자 역학(quantum mechanics) 사이에는 근본적인 비호환성이 존재하는 것으로 나타났습니다.

1930년대에, 정수 집합에 대go 이중-타격 대문자 Z는 에드문트 란다우(Edmund Landau)에 의해 만들어졌습니다. 니콜라 부르바키(Nicolas Bourbaki)는 유리수 집합에 대해 이중-타격 대문자 Q를 만들었습니다. 1935년에, 게르하르트 겐첸(Gerhard Gentzen)은 보편 한정어(universal quantifier)를 만들었습니다. 1936년에, 타르스키의 증명-불가능성 정리(Tarski's undefinability theorem)가 알프레트 타르스키(Alfred Tarski)에 의해 명시되고 입증되었습니다.^{[note 90]} 1938년에, 괴델(Gödel)은 "선택의 공리와 일반화된 연속체-가설의 일관성"이라는 논문에서 구성-가능 우주(constructible universe)를 제안합니다. 앙드레 베유(André Weil)와 니콜라 부르바키(Nicolas Bourbaki)는 1939년에 빈 집합(empty set) 기호를 개발했을 것입니다. 같은 해, 네이선 제이컵슨(Nathan Jacobson)은 복소수(complex number) 집합에 대해 이중-타격 대문자 C를 만들었을 것입니다.

1930년대 즈음에, 포크트 표기법(Voigt notation)은 그것의 차수를 줄임으로써 대칭 텐서(symmetric tensor)를 나타내기 위한 방법으로 다중선형 대수(multilinear algebra)에 대해 개발되었을 것입니다.^{[note 91]} 숀피스 표기법(Schönflies notation)은 점 그룹(point group)을 설명하기 위해 사용되는 두 가지 규칙 중 하나가 되었습니다 (다른 하나는 헤어만–모갱 표기법(Hermann–Mauguin notation)입니다).^{[note 92]} 역시 이 시기에, 반 데르 바르던 표기법(van der Waerden notation)은 사-차원 시공간에서 둘의-성분 스피너(spinor) (바일 스피너)의 사용법에 대해 대중화되었습니다.^[122]^[123] 아런트 헤이팅(Arend Heyting)은 헤이팅 대수(Heyting algebra)와 헤이팅 산술(Heyting arithmetic)을 도입했을 것입니다.

화살표, 예를 들어, →는 1936년에 외위스테인 오레(Øystein Ore)에 의해 특정 원소의 이미지를 표시하기 위해 함수 표기법(function notation)에 대해 개발되었습니다.^{[note 93]}^{[note 94]} 나중에, 1940년에, 그것은 비톨트 후레비치(Witold Hurewicz)의 연구를 통해 그것의 현재 형식, 예를 들어, f: X → Y를 취했습니다. 베르너 하이젠베르크(Werner Heisenberg)는, 1941년에, 입자 상호작용의 S-행렬 이론(S-matrix theory)을 제안했습니다.

괄–호 표기법(bra–ket notation) (디랙 표기법)은 각진 괄호(angle brackets)와 세로 막대(vertical bar)로 구성된 양자 상태(quantum state)를 설명하는 표준 표기법입니다. 그것은 역시 추상 벡터(vectors)와 선형 함수형(linear functional)을 나타내기 위해 사용될 수 있습니다. 그것은 둘의 상태의 안의 곱(inner product) (또는 복소 벡터 공간 위에 점 곱(dot product))이 왼쪽 부분, ⟨φ| 및 오른쪽 부분, |ψ⟩으로 구성된 ⟨bra|ket⟩에 의해 표시되기 때문에 그렇게 불립니다.^{[note 95]} 그 표기법은 1939년에 폴 디랙(Paul Dirac)에 의해 도입되었지만,^[124] 그 표기법은 거의 100년 전에 그의 내부 제품에 대해 [φ|ψ] 표기법의 그라스만(Grassmann)의 사용에서 선구자를 가졌습니다.^[125]

괄–호 표기법은 양자 역학(quantum mechanics)에서 널리 퍼져 있습니다: 현대 물리학의 많은 부분을 포함하는 양자 역학을 사용하여 설명되는 거의 모든 각 현상은 보통 괄–호 표기법의 도움과 함께 설명됩니다. 그 표기법은 인코딩된 추상적 표현-독립성을 수립하여, 관련된 선형 공간(linear space)의 본성(nature)에 많은 고민(ado)이나 과도한 의존없이 다양한 특정 표현 (예를 들어, x, 또는 p, 또는 고유함수(eigenfunction) 기반)을 생성합니다. 중첩 표현식 ⟨φ|ψ⟩는 전형적으로 상태(state) ψ에 대해 상태 ϕ로의 붕괴(collapse)할 확률 진폭(probability amplitude)으로 해석됩니다. 파인만 슬래시 표기법(Feynman slash notation) (디랙 슬래시 표기법^[126])은 양자 필드 이론(quantum field theory)에서 디랙 필드(Dirac field) 연구에 대해 리처드 파인만(Richard Feynman)에 의해 개발되었습니다.

1948년에, 발렌티네 바르그만(Valentine Bargmann)과 유진 위그너(Eugene Wigner)는 자유 입자(free particle)를 설명하기 위해 상대론적(relativistic) 바르그만–위그너 방정식(Bargmann–Wigner equations)을 제안했었고 그 방정식은 여러-성분 스피너 필드(spinor field) 파동함수(wavefunction)의 형식에 있습니다. 1950년에, 윌리엄 밸런스 더글러스 호지(William Vallance Douglas Hodge)는 Proceedings of the International Congress of Mathematicians에서 "대수적 다양체의 토폴로지적 불변"을 발표했습니다. 1954년과 1957년 사이에, 에우제니오 칼라비(Eugenio Calabi)는 켈러 메트릭(Kähler metric)에 대해 칼라비 추측(Calabi conjecture)과 칼라비–야우 매니폴드(Calabi–Yau manifold) 개발에 대해 연구했습니다. 1957년에, 툴리오 레제(Tullio Regge)는 슈뢰딩거 방정식(Schrödinger equation)에서 잠재적 산란의 수학적 속성을 공식화했습니다.^{[note 96]} 스탠리 만델스탐(Stanley Mandelstam)은, 레제와 함께, 강력한 상호작용 현상학의 레제 이론(Regge theory)의 초기 개발이었습니다. 1958년에, 머리 겔-맨(Murray Gell-Mann)과 리처드 파인만(Richard Feynman)은, 조지 수다르샨(George Sudarshan)과 로버트 마샥(Robert Marshak)과 함께, 물리학에서 약한 상호작용(weak interaction)의 카이럴 구조(chiral structures)를 추론했습니다. 제프리 추(Geoffrey Chew)는, 다른 사람들과 함께, 1960년에 강력한 상호작용(strong interaction)에 대해 행렬 표기법과 관련된 부트스트랩 원리(bootstrap principle)를 장려했을 것입니다. 1960년대에, 집합-구성 표기법(set-builder notation)은 그것의 구성원이 만족시켜야 하는 속성을 말함으로써 집합(set)을 설명하는 데 개발되었습니다. 역시 1960년대에, 텐서는 모노이드 카테고리(monoidal category)의 개념을 수단으로 카테고리 이론(category theory) 내에서 추상화되었습니다. 나중에, 다중-색인 표기법(multi-index notation)은 정수 인덱스(index)의 개념을 인덱스의 순서화된 튜플(tuple)로 추상화함으로써로써 다변수 미적분학(multivariable calculus), 부분 미분 방정식(partial differential equation), 및 분포(distributions)의 이론에서 사용되는 전통적인 개념을 제거합니다.

Modern mathematical notation

특수 상대성(special relativity), 전자기학(electromagnetism), 및 파동 이론(wave theory)의 현대 수학에서, 달랑베르 연산자(d'Alembert operator)는 민코프스키 공간(Minkowski space)의 라플라스 연산자(Laplace operator)입니다.^{[note 97]}^{[note 98]} 레비-치비타 기호(Levi-Civita symbol)는 텐서 미적분학(tensor calculus)에서 사용됩니다.^{[note 99]}

양자 전기-동역학의 섭동 급수에서 임의의 순서에서 유한한 전체 로렌츠 공분산(Lorentz covariance) 공식 이후, 신-이치로 토모나가(Sin-Itiro Tomonaga), 줄리언 슈윙거(Julian Schwinger), 및 리처드 파인만(Richard Feynman)은 1965년에 물리학에서 노벨 상(Nobel prize in physics)을 공동으로 수상했습니다.^[127] 그들의 공헌과, 프리먼 다이슨(Freeman Dyson)의 공헌은, 섭동 이론(perturbation theory)의 임의의 순서에서 관측의 계산을 허용하는 양자 전기동역학의 공변 및 게이지 불변(gauge invariant) 공식에 관한 것이었습니다. 그의 다이어그램(diagrams)을 기반으로 한 파인만의 수학적 기법은 처음에는 슈윙거(Schwinger)와 토모나가(Tomonaga)의 필드-이론적, 연산자(operator)-기반 접근 방식과 매우 다른 것처럼 보였지만, 프리먼 다이슨(Freeman Dyson)은 나중에 두 접근 방식이 동등함을 보여주었습니다. 적분(integral)을 통해 이론에서 나타나는 특정 발산에 물리적 의미를 부여하기 위한 필요성, 재정규화(renormalization)는 이후 양자 필드 이론(quantum field theory)의 근본적인 관점 중 하나가 되었고 이론의 일반적인 수용가능성에 대해 기준으로 고려되게 되었습니다. 양자 전기동역학은 후속 양자 필드 이론에 대해 모델이자 템플릿으로 역할을 했습니다. 피터 힉스(Peter Higgs), 제프리 골드스톤(Jeffrey Goldstone), 및 다른 사람들, 셸던 글래쇼(Sheldon Glashow), 스티븐 와인버그(Steven Weinberg), 및 압두스 살람(Abdus Salam)은 약한 핵의 힘(weak nuclear force)과 양자 전기역역학이 단일 전기약한 힘(electroweak force)으로 병합될 수 있는 방법을 독립적으로 보여주었습니다. 1960년대 후반에, 입자 동물원(particle zoo)은 쿼크(quarks)의 발견 전에 알려진 기본 입자(elementary particle)로 구성되었습니다.

표준 모델(Standard Model)을 향한 한 걸음은, 1960년에, 전자기(electromagnetic)와 약한 상호작용(weak interaction)을 결합하기 위한 셸던 글래쇼(Sheldon Glashow)의 발견이었습니다.^[128] 1967년에, 스티븐 와인버그(Steven Weinberg)와^[129] 압두스 살람(Abdus Salam)은^[130] 힉스 메커니즘(Higgs mechanism)을^[131]^[132]^[133] 글래쇼의 전기약한 이론(electroweak theory)에 통합하여, 그것을 현대적인 형식으로 제공했습니다. 힉스 메커니즘은 표준 모델에서 모든 기본 입자(elementary particle)의 질량(mass)을 발생시키는 것으로 믿어졌습니다. 이것은 W 및 Z 보존스(W and Z bosons)의 질량과 페르미온(fermion)의 질량 – 쿼크와 렙톤을 포함합니다. 역시 1967년에, 브라이스 디윗(Bryce DeWitt)는 "아인슈타인–슈뢰딩거 방정식" (나중에 "휠러–디윗 방정식"으로 다시 이름지어짐)이라는 이름 아래에 그의 방정식을 발표했습니다.^[134] 1969년에, 요이치로 난부(Yoichiro Nambu), 홀게르 베크 닐센(Holger Bech Nielsen), 및 레너드 서스킨드(Leonard Susskind)는 끈(string)의 관점에서 공간과 시간을 설명했습니다. 1970년에, 피에르 라몽(Pierre Ramond)는 이-차원 초월대칭을 개발했습니다. 미치오 카쿠(Michio Kaku)와 케지 키까와(Keiji Kikkawa)는 이후 끈 변형을 공식화했습니다. 1972년에, 마이클 아틴(Michael Artin), 알렉상드르 그로텐디크(Alexandre Grothendieck), 장-루이 베르디에(Jean-Louis Verdier)는 그로텐디크 우주(Grothendieck universe)를 제안합니다.^[135]

Z
보손 교환으로 인한 중성 약한 전류(neutral weak currents)가 1973년 CERN에서 발견되었고,^[136]^[137]^[138]^[139] 전기약한 이론은 널리 받아들여졌고 글래쇼(Glashow), 살람(Salam), 와인버그(Weinberg)는 이를 발견한 공로로 1979년 물리학에서 노벨 상(Nobel Prize in Physics)을 공동 수상했습니다. 많은 사람들이 기여한 강한 상호작용(strong interaction)의 이론은 1973–74년경 현대적인 형식을 갖추었습니다. 양자 색동역학(quantum chromodynamics)의 확립과 함께, 중력을 제외한 모든 힘을 성공적으로 설명되었고, 적용되도록 설계된 도메인 내에서 일반적으로 수락되게 남아있는 게이지 불변(gauge invariance)의 수학을 기반으로 하는 "표준 모델"의 확립을 허용하는 일련의 기본과 교환 입자의 집합을 완성되었습니다. 적용되도록 설계된 도메인 내에서. 1970년대 후반에, 윌리엄 서스턴(William Thurston)은 쌍곡선화 정리(hyperbolization theorem)를 갖는 매듭의 연구(study of knots)에 쌍곡선 기하학(hyperbolic geometry)을 도입했습니다. 서스턴에 의해 발명된 오비폴드 표기법(orbifold notation) 시스템은 상수 곡률의 이-차원 공간에서 대칭 그룹(symmetry groups)의 유형을 나타내기 위해 개발되어 왔습니다. 1978년에, 추 청퉁(Shing-Tung Yau)은 칼라비 추측(Calabi conjecture)이 리치 플랫(Ricci flat) 메트릭을 가지고 있다고 추론했습니다. 1979년에, 대니얼 프리댄(Daniel Friedan)은 끈 이론(string theory)의 운동 방정식이 일반 상대성(General Relativity)의 아인슈타인 방정식(Einstein equations)의 추상화임을 보여주었습니다.

최초의 초월끈 혁명(first superstring revolution)은 1984년과 1986년 사이에 개발된 수학적 방정식으로 구성됩니다. 1984년에, 본 존스(Vaughan Jones)는 존 다항식(Jones polynomial)을 추론했었고 에드워드 위튼(Edward Witten), 막심 콘체비치(Maxim Kontsevich), 및 다른 사람들의 후속 공헌은 통계적 역학(statistical mechanics)에서 매듭 이론과 수학적 방법과 양자 필드 이론 사이의 깊은 연관성을 밝혔습니다. 끈 이론(string theory)에 따르면, "입자 동물원"에서 모든 입자는 공통 조상, 즉 진동하는 끈(vibrating string)을 가지고 있습니다. 1985년에, 필립 칸델라스(Philip Candelas), 게리 호로위츠(Gary Horowitz),^[140] 앤드루 스트로민저(Andrew Strominger), 및 에드워드 위튼(Edward Witten)은 "초월끈에 대해 진공 구성(Vacuum configurations for superstrings)"을 발표했을 것입니다.^[141] 나중에, 티트라트 형식주의(tetrad formalism) (티트라트 인덱스 표기법)는 좌표 기저(coordinate basis)의 선택을 접 다발에 대해 지역적 기저의 덜 제한적인 선택으로 대체하는 일반 상대성(general relativity)에 대한 접근 방식으로 도입되었을 것입니다.^{[note 102]}^[142]

1990년대에, 로저 펜로즈(Roger Penrose)는 펜로즈 그래픽 표기법(Penrose graphical notation) (텐서 다이어그램 표기법)을 다중선형 함수(multilinear function) 또는 텐서(tensor)의 일반적으로 손으로 쓴, 시각적 묘사로 제안했을 것입니다.^[143] 펜로즈는 역시 추상적 인덱스 표기법(abstract index notation)을 도입했을 것입니다.^{[note 103]} 1995년에, 에드워드 위튼(Edward Witten)은 M-이론(M-theory)을 제안하고 그 후 그것을 두 번째 초월끈 혁명(second superstring revolution)을 시작하는 관찰된 이중성(dualities)을 설명하기 위해 사용했습니다.^{[note 104]}

존 콘웨이(John Conway)는 콘웨이 체인된 화살표 표기법(Conway chained arrow notation), 매듭 이론의 콘웨이 표기법(Conway notation of knot theory), 및 콘웨이 다면체 표기법(Conway polyhedron notation)을 포함하여 다양한 표기법을 추가했을 것입니다. 콕세터 표기법(Coxeter notation) 시스템은 콕세터 그룹(Coxeter group)의 기본 반사와 사이의 각도를 설명하는 대칭 그룹을 분류합니다. 그것은 특정 부분그룹을 나타내는 수정자와 함께 괄호화된 표기법을 사용합니다. 그 표기법은 콕세터와 노먼 존슨(Norman Johnson)이 그것을 보다 포괄적으로 정의한 후 그들의 이름을 따서 지어졌습니다.

조합론적(Combinatorial) LCF 표기법(LCF notation)은^{[note 105]} 해밀턴(Hamiltonian)인 삼차 그래프(cubic graph)의 표현을 위해 개발되어 왔습니다.^[144]^[145] 순환 표기법(cycle notation)은 순열(permutation)을 구성 순환(cycles)의 관점에서 기록하는 규칙입니다.^[146] 이것은 역시 원형 표기법(circular notation)이라고 불리고 그 순열은 순환 또는 원형 순열이라고 불립니다.^[147]

Computers and markup notation

1931년에, IBM은 IBM 601 Multiplying Punch를 생산합니다; 그것은 카드에서 둘의 숫자, 최대 8 자릿수 길이를 읽고 그것들의 곱을 같은 카드에 펀칭할 수 있는 전자역학의 기계입니다.^[148] 1934년에, 월레스 에커트(Wallace Eckert)는 미분 방정식의 적분을 자동화하기 위해 조작된 IBM 601 Multiplying Punch를 사용했습니다.^[149] 1936년에, 앨런 튜링(Alan Turing)은 "On Computable Numbers, With an Application to the Entscheidungsproblem"을 발표했습니다.^[150]^{[note 106]} 디지털 컴퓨터와 컴퓨터 과학의 개척자,^{[note 107]} 존 폰 노이만(John von Neumann)은 1945년에 불완전한(incomplete) First Draft of a Report on the EDVAC를 씁니다. EDVAC에 대한 보고서의 첫 번째 초안. 1962년에, 케네스 아이버슨(Kenneth E. Iverson)은 그의 학생들에게 가르쳤던 배열을 조작하기 위해 APL이 되었던 적분 부분 표기법을 개발했었고, 그의 책 A Programming Language에 설명했습니다. 1970년에, 에드거 커드(Edgar F. Codd)는 데이터베이스 질의 언어(database query language)에 대해 데이터의 관계형 모델로 관계형 대수학(relational algebra)을 제안했습니다. 1971년에, 스티븐 쿡(Stephen Cook)은 "정리 증명 절차의 복잡성"을 출판했습니다.^[151] 1970년대 컴퓨터 아키텍처(computer architecture) 내에서, 인용-부호 표기법(quote notation)이 유리수(rational number)의 숫자 시스템을 나타내기 위해 개발되었습니다. 역시 이 10년 동안, (오래 전에 APL 언어와 마찬가지로) Z 표기법(Z notation)은 많은 비-아스키 기호를 사용했으며, 그 사양은 아스키와 레이텍에서 Z 표기법 기호를 렌더링하기 위한 제안을 포함하고 있습니다. 현재 다양한 C 수학 함수 (Math.h)와 수치 라이브러리(numerical libraries)가 있습니다. 그것들은 수치(numerical) 계산을 수행하기 위해 소프트웨어 개발(software development)에 사용되는 라이브러리(libraries)입니다. 이들 계산은 기호 실행(symbolic execution)에 의해 처리될 수 있습니다; 어떤 입력이 프로그램의 각 부분을 실행하게 하는지를 결정하기 위해 프로그램을 분석합니다. Mathematica와 SymPy는 기호적 수학(symbolic mathematics)에 기반한 계산 소프트웨어 프로그램의 예제입니다.

Future of mathematical notation

수학 표기법의 역사에서, 서명의 기호 표기법은 컴퓨터 시각화 시스템의 등장과 함께 완전한 원을 이루었습니다. 그 표기법은 칼라비-야우(Calabi-Yau) 매니폴드(manifold)의 일부 투영을 렌더링하는 것과 같은 추상적 시각화에 적용될 수 있습니다. 수학적 상상력에 적절하게 속하는 추상적인 시각화(abstract visualization)의 예제는 컴퓨터 그래픽(computer graphics)에서 찾아질 수 있습니다. 예를 들어, 연구 주제에 대해 측정이 실제로는 확률 변수(random variable)이고 실제로 보통의 수학적 함수(mathematical function)가 아닐 때 그러한 모델에 대해 필요성은 풍부합니다.

Notes

^ Or the Middle Ages.
^ Such characters, in fact, are preserved with little alteration in the Roman notation, an account of which may be found in John Leslie's Philosophy of Arithmetic.
^ Number theory is branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well as the properties of objects made out of integers (e.g., rational numbers) or defined as generalizations of the integers (e.g., algebraic integers).
^ Greek: μή μου τοὺς κύκλους τάραττε
^ That is, $a^{2}+b^{2}=c^{2}$ .
^ Magnitude (mathematics), the relative size of an object ; Magnitude (vector), a term for the size or length of a vector; Scalar (mathematics), a quantity defined only by its magnitude; Euclidean vector, a quantity defined by both its magnitude and its direction; Order of magnitude, the class of scale having a fixed value ratio to the preceding class.
^ Autolycus' On the Moving Sphere is another ancient mathematical manuscript of the time.
^ Proclus, a Greek mathematician who lived several centuries after Euclid, wrote in his commentary of the Elements: "Euclid, who put together the Elements, collecting many of Eudoxus' theorems, perfecting many of Theaetetus', and also bringing to irrefragable demonstration the things which were only somewhat loosely proved by his predecessors".
^ The expression:
$2x^{4}+3x^{3}-4x^{2}+5x-6$
would be written as:
SS2 C3 x5 M S4 u6
.^{[citation needed]}
^ such as the wheel and axle
^ such as the rule, square, compasses, water level (reed level), and plumb-bob.
^ The area of the square described on the hypotenuse of a right-angled triangle is equal to the sum of the areas of the squares described on the sides
^ Al-Kindi also introduced cryptanalysis and frequency analysis.
^ Something close to a proof by mathematical induction appears in a book written by Al-Karaji around 1000 AD, who used it to prove the binomial theorem, Pascal's triangle, and the sum of integral cubes.
^ He thus came close to finding a general formula for the integrals of polynomials, but he was not concerned with any polynomials higher than the fourth degree.
^ a book about what he perceived as flaws in Euclid's Elements, especially the parallel postulate
^ translated into Latin by Robert of Chester
^ translated in various versions by Adelard of Bath, Herman of Carinthia, and Gerard of Cremona
^ His own personal use started around 1351.
^ Summa de Arithmetica: Geometria Proportioni et Proportionalita. Tr. Sum of Arithmetic: Geometry in proportions and proportionality.
^ Much of the work originated from Piero della Francesca whom he appropriated and purloined.
^ This was a special case of the methods given many centuries later by Ruffini and Horner.
^ That is, ${\sqrt {~}}$ .
^ Because, it is thought, it resembled a lowercase "r" (for "radix").
^ Published in Description of the Marvelous Canon of Logarithms
^ That is,
∷
^ see Law of Continuity.
^ Using Cartesian coordinates on the plane, the distance between two points (x₁, y₁) and (x₂, y₂) is defined by the formula:
$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}},$
which can be viewed as a version of the Pythagorean theorem.
^ Further steps in abstraction were taken by Lobachevsky, Bolyai, Riemann, and Gauss who generalised the concepts of geometry to develop non-Euclidean geometries.
^ Now called Pascal's triangle.
^ For example, the "problem of points".
^ That is, ${\infty }$ .
^ For example, ${\frac {1}{\infty }}.$
^ Original title, "De ratiociniis in ludo aleae"
^ For example, the derivative of the function x would be written as ${\dot {x}}$ . The second derivative of x would be written as ${\ddot {x}}$ , etc.
^ For example, the derivative of the function x with respect to the variable t in Leibniz's notation would be written as ${dx \over dt}$ .
^ That is, $\int _{-N}^{N}f(x)\,dx$ .
^ See also: List of representations of e
^ Thus $f(x)$ denotes the mathematical result of the performance of the operation $f$ upon the subject $x$ . If upon this result the same operation were repeated, the new result would be expressed by $f[f(x)]$ , or more concisely by $f^{2}(x)$ , and so on. The quantity $x$ itself regarded as the result of the same operation $f$ upon some other function; the proper symbol for which is, by analogy, $f^{-1}(x)$ . Thus $f$ and $f^{-1}$ are symbols of inverse operations, the former cancelling the effect of the latter on the subject $x$ . $f(x)$ and $f^{-1}(x)$ in a similar manner are termed inverse functions.
^ That is, $\Delta f(p)$
^ That is, ${\sqrt {-1}}$
^ Today, the symbol created by John Wallis, $\infty$ , is used for infinity.
^ As in, $\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}$
^ Capital-sigma notation uses a symbol that compactly represents summation of many similar terms: the summation symbol, Σ, an enlarged form of the upright capital Greek letter Sigma. This is defined as:

$\sum _{i=m}^{n}a_{i}=a_{m}+a_{m+1}+a_{m+2}+\cdots +a_{n-1}+a_{n}.$

Where, i represents the index of summation; a_i is an indexed variable representing each successive term in the series; m is the lower bound of summation, and n is the upper bound of summation. The "i = m" under the summation symbol means that the index i starts out equal to m. The index, i, is incremented by 1 for each successive term, stopping when i = n.
^ That is, $n!=\int _{0}^{1}(-\ln s)^{n}\,{\rm {d}}s$ .
valid for n > 0.
^ That is,
∝
^ Proportionality is the ratio of one quantity to another, especially the ratio of a part compared to a whole. In a mathematical context, a proportion is the statement of equality between two ratios; See Proportionality (mathematics), the relationship of two variables whose ratio is constant. See also aspect ratio, geometric proportions.
^ The curly d or Jacobi's delta.
^ About the proof of Wilson's theorem. Disquisitiones Arithmeticae (1801) Article 76
^ Galois theory and Galois geometry is named after him.
^ That is, "subset of" and "superset of"; This would later be redeveloped by Ernst Schröder.
^ A science of numbers that uses methods from mathematical analysis to solve problems about the integers.
^ Quoted in Robert Perceval Graves' Life of Sir William Rowan Hamilton (3 volumes, 1882, 1885, 1889)
^ That is, $\nabla$ (or, later called del, ∇)
^ See Hamiltonian (quantum mechanics).
^ That is, $i^{2}=j^{2}=k^{2}=ijk=-1$
^ Though his use describes something different from what is now meant by a tensor. Namely, the norm operation in a certain type of algebraic system (now known as a Clifford algebra).
^ That is,
$t=w+xi+yj+zk,\quad w,x,y,z\in \mathbb {R}$
where
$ij=ji=k,\quad i^{2}=-1,\quad j^{2}=+1.$
^ This is Latin for "womb".
^ That is, $q=w+xi+yj+zk$
^ Clifford intersected algebra with Hamilton's quaternions by replacing Hermann Grassmann's rule e_pe_p = 0 by the rule e_pe_p = 1. For more details, see exterior algebra.
^ See: Phasor, Group (mathematics), Signal velocity, Polyphase system, Harmonic oscillator, and RLC series circuit
^ Or the concept of a fourth spatial dimension. See also: Spacetime, the unification of time and space as a four-dimensional continuum; and, Minkowski space, the mathematical setting for special relativity.
^ See also: Mathematic fields and Field extension
^ Comment after the proof that 1+1=2, completed in Principia mathematica, by Alfred North Whitehead ... and Bertrand Russell. Volume II, 1st edition (1912)
^ This raises questions of the pure existence theorems.
^ Peano's Formulario Mathematico, though less popular than Russell's work, continued through five editions. The fifth appeared in 1908 and included 4200 formulas and theorems.
^ Inventor of set theory
^ Transfinite arithmetic is the generalization of elementary arithmetic to infinite quantities like infinite sets; See Transfinite numbers, Transfinite induction, and Transfinite interpolation. See also Ordinal arithmetic.
^ Such as Max Dehn, J. W. Alexander, and others.
^ Such as the Alexander polynomial.
^ (German: Algebraische Theorie der Körper)
^ In this paper Steinitz axiomatically studied the properties of fields and defined many important field theoretic concepts like prime field, perfect field and the transcendence degree of a field extension.
^ The indices range over set ${1, 2, 3$ },
$y=\sum _{i=1}^{3}c_{i}x^{i}=c_{1}x^{1}+c_{2}x^{2}+c_{3}x^{3}$
is reduced by the convention to:
$y=c_{i}x^{i}\,.$
Upper indices are not exponents but are indices of coordinates, coefficients or basis vectors.
See also: Ricci calculus
^ Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields. See also: Synge J.L.; Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. pp. 6–108.
^ Here a logical constant is a symbol in symbolic logic that has the same meaning in all models, such as the symbol "=" for "equals".
A constant, in a mathematical context, is a number that arises naturally in mathematics, such as π or e; Such mathematics constant value do not change. It can mean polynomial constant term (the term of degree 0) or the constant of integration, a free parameter arising in integration.
Related, the physical constant are a physical quantity generally believed to be universal and unchanging. Programming constants are a values that, unlike a variable, cannot be reassociated with a different value.
^ Though not an index term, keywords are terms that represent information. A keyword is a word with special meaning (this is a semantic definition), while syntactically these are terminal symbols in the phrase grammar. See reserved word for the related concept.
^ Most of these symbols can be found in propositional calculus, a formal system described as ${\mathcal {L}}={\mathcal {L}}\ (\mathrm {A} ,\ \Omega ,\ \mathrm {Z} ,\ \mathrm {I} )$ . $\mathrm {A}$ is the set of elements, such as the a in the example with Boolean algebra above. $\Omega$ is the set that contains the subsets that contain operations, such as $\lor$ or $\land$ . $\mathrm {Z}$ contains the inference rules, which are the rules dictating how inferences may be logically made, and $\mathrm {I}$ contains the axioms. See also: Basic and Derived Argument Forms.
^ Usually denoted by x, y, z, or other lowercase letters
Here a symbols that represents a quantity in a mathematical expression, a mathematical variable as used in many sciences.
Variables can be symbolic name associated with a value and whose associated value may be changed, known in computer science as a variable reference. A variable can also be the operationalized way in which the attribute is represented for further data processing (e.g., a logical set of attributes). See also: Dependent and independent variables in statistics.
^ Usually denoted by an uppercase letter followed by a list of variables, such as P(x) or Q(y,z)
Here a mathematical logic predicate, a fundamental concept in first-order logic. Grammatical predicates are grammatical components of a sentence.
Related is the syntactic predicate in parser technology which are guidelines for the parser process. In computer programming, a branch predication allows a choice to execute or not to execute a given instruction based on the content of a machine register.
^ Representing ALL and EXISTS
^ e.g. ∃ for "there exists" and ∀ for "for all"
^ See also: Dialetheism, Contradiction, and Paradox
^ Related, facetious abstract nonsense describes certain kinds of arguments and methods related to category theory which resembles comical literary non-sequitur devices (not illogical non-sequiturs).
^ Gödel's incompleteness theorems shows that Hilbert's program to find a complete and consistent set of axioms for all mathematics is impossible, giving a contested negative answer to Hilbert's second problem
^ For example, take the statement "There exists a number x such that it is not y". Using the symbols of propositional calculus, this would become: $(\exists x)(x=\lnot y)$ .
If the Gödel numbers replace the symbols, it becomes: $\{8,4,11,9,8,11,5,1,13,9\}$ .
There are ten numbers, so the ten prime numbers are found and these are: $\{2,3,5,7,11,13,17,19,23,29\}$ .
Then, the Gödel numbers are made the powers of the respective primes and multiplied, giving: $2^{8}\times 3^{4}\times 5^{11}\times 7^{9}\times 11^{8}\times 13^{11}\times 17^{5}\times 19^{1}\times 23^{13}\times 29^{9}$ .
The resulting number is approximately $3.096262735\times 10^{78}$ .
^ The Klein–Gordon equation is:

${\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\psi -\nabla ^{2}\psi +{\frac {m^{2}c^{2}}{\hbar ^{2}}}\psi =0.$
^ The Dirac equation in the form originally proposed by Dirac is:

$\left(\beta mc^{2}+\sum _{k=1}^{3}\alpha _{k}p_{k}\,c\right)\psi (\mathbf {x} ,t)=i\hbar {\frac {\partial \psi (\mathbf {x} ,t)}{\partial t}}$

where, $ψ = ψ(x, t)$ is the wave function for the electron, $x$ and $t$ are the space and time coordinates, $m$ is the rest mass of the electron, $p$ is the momentum, understood to be the momentum operator in the Schrödinger theory, $c$ is the speed of light, and $ħ = h /2 π$ is the reduced Planck constant.
^ That is,

$\partial _{\mu }(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu })+\left({\frac {mc}{\hbar }}\right)^{2}A^{\nu }=0$
^ The theorem applies more generally to any sufficiently strong formal system, showing that truth in the standard model of the system cannot be defined within the system.
^ Named to honor Voigt's 1898 work.
^ Named after Arthur Moritz Schoenflies
^ See Galois connections.
^ Oystein Ore would also write "Number Theory and Its History".
^ $\langle \phi |\psi \rangle$
^ That the scattering amplitude can be thought of as an analytic function of the angular momentum, and that the position of the poles determine power-law growth rates of the amplitude in the purely mathematical region of large values of the cosine of the scattering angle.
^ That is, $\scriptstyle \Box$
^ Also known as the d'Alembertian or wave operator.
^ Also known as, "permutation symbol" (see: permutation), "antisymmetric symbol" (see: antisymmetric), or "alternating symbol"
^ Note that "masses" (e.g., the coherent non-definite body shape) of particles are periodically reevaluated by the scientific community. The values may have been adjusted; adjustment by operations carried out on instruments in order that it provides given indications corresponding to given values of the measurand. In engineering, mathematics, and geodesy, the optimal parameter such estimation of a mathematical model so as to best fit a data set.
^ For the consensus, see Particle Data Group.
^ A locally defined set of four linearly independent vector fields called a tetrad
^ His usage of the Einstein summation was in order to offset the inconvenience in describing contractions and covariant differentiation in modern abstract tensor notation, while maintaining explicit covariance of the expressions involved.
^ See also: String theory landscape and Swampland
^ Devised by Joshua Lederberg and extended by Coxeter and Frucht
^ And, in 1938, Turing, A. M. (1938). "On Computable Numbers, with an Application to the Entscheidungsproblem. A Correction". Proceedings of the London Mathematical Society. s2-43: 544–546. doi:10.1112/plms/s2-43.6.544..
^ Among von Neumann's other contributions include the application of operator theory to quantum mechanics, in the development of functional analysis, and on various forms of operator theory.

References and citations

General

Florian Cajori (1929) A History of Mathematical Notations, 2 vols. Dover reprint in 1 vol., 1993. ISBN 0-486-67766-4.

Citations

^ Florian Cajori. A History of Mathematical Notations: Two Volumes in One. Cosimo, Inc., Dec 1, 2011
^ A Dictionary of Science, Literature, & Art, Volume 2. Edited by William Thomas Brande, George William Cox. Pg 683
^ "Notation - from Wolfram MathWorld". Mathworld.wolfram.com. Retrieved 2014-06-24.
^ Diophantos of Alexandria: A Study in the History of Greek Algebra. By Sir Thomas Little Heath. Pg 77.
^ Mathematics: Its Power and Utility. By Karl J. Smith. Pg 86.
^ The Commercial Revolution and the Beginnings of Western Mathematics in Renaissance Florence, 1300–1500. Warren Van Egmond. 1976. Page 233.
^ Solomon Gandz. "The Sources of al-Khowarizmi's Algebra"
^ Encyclopædia Americana. By Thomas Gamaliel Bradford. Pg 314
^ Mathematical Excursion, Enhanced Edition: Enhanced Webassign Edition By Richard N. Aufmann, Joanne Lockwood, Richard D. Nation, Daniel K. Cleg. Pg 186
^ Mathematics in Egypt and Mesopotamia^{[dead link]}
^ Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "Mesopotamia" p. 25.
^ Duncan J. Melville (2003). Third Millennium Chronology, Third Millennium Mathematics. St. Lawrence University.
^ Aaboe, Asger (1998). Episodes from the Early History of Mathematics. New York: Random House. pp. 30–31.
^ Heath. A Manual of Greek Mathematics. p. 5.
^ Sir Thomas L. Heath, A Manual of Greek Mathematics, Dover, 1963, p. 1: "In the case of mathematics, it is the Greek contribution which it is most essential to know, for it was the Greeks who made mathematics a science."
^ ^a ^b The new encyclopædia; or, Universal dictionary of arts and sciences. By Encyclopaedia Perthensi. Pg 49
^ Calinger, Ronald (1999). A Contextual History of Mathematics. Prentice-Hall. p. 150. ISBN 0-02-318285-7. Shortly after Euclid, compiler of the definitive textbook, came Archimedes of Syracuse (ca. 287 212 BC), the most original and profound mathematician of antiquity.
^ "Archimedes of Syracuse". The MacTutor History of Mathematics archive. January 1999. Retrieved 2008-06-09.
^ O'Connor, J.J.; Robertson, E.F. (February 1996). "A history of calculus". University of St Andrews. Archived from the original on 15 July 2007. Retrieved 2007-08-07. {{cite web}}: Unknown parameter |deadurl= ignored (|url-status= suggested) (help)
^ "Proclus' Summary". Gap.dcs.st-and.ac.uk. Archived from the original on 23 September 2015. Retrieved 24 June 2014. {{cite web}}: Unknown parameter |dead-url= ignored (|url-status= suggested) (help)
^ Caldwell, John (1981) "The De Institutione Arithmetica and the De Institutione Musica", pp. 135–54 in Margaret Gibson, ed., Boethius: His Life, Thought, and Influence, (Oxford: Basil Blackwell).
^ Folkerts, Menso, "Boethius" Geometrie II, (Wiesbaden: Franz Steiner Verlag, 1970).
^ Mathematics and Measurement By Oswald Ashton Wentworth Dilk. Pg 14
^ ^a ^b ^c ^d ^e A dictionary of science, literature and art, ed. by W.T. Brande. Pg 683
^ Boyer, Carl B. A History of Mathematics, 2nd edition, John Wiley & Sons, Inc., 1991.
^ Diophantine Equations. Submitted by: Aaron Zerhusen, Chris Rakes, & Shasta Meece. MA 330-002. Dr. Carl Eberhart. February 16, 1999.
^ A History of Greek Mathematics: From Aristarchus to Diophantus. By Sir Thomas Little Heath. Pg 456
^ A History of Greek Mathematics: From Aristarchus to Diophantus. By Sir Thomas Little Heath. Pg 458
^ The American Mathematical Monthly, Volume 16. Pg 131
^ "Overview of Chinese mathematics". Groups.dcs.st-and.ac.uk. Retrieved 2014-06-24.
^ George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Penguin Books, London, 1991, pp.140—148
^ Georges Ifrah, Universalgeschichte der Zahlen, Campus, Frankfurt/New York, 1986, pp.428—437
^ "Frank J. Swetz and T. I. Kao: Was Pythagoras Chinese?". Psupress.psu.edu. Retrieved 2014-06-24.
^ ^a ^b Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd..
^ Sal Restivo
^ Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.
^ Marcel Gauchet, 151.
^ Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "China and India" p. 221. (cf., "he was the first one to give a general solution of the linear Diophantine equation ax + by = c, where a, b, and c are integers. [...] It is greatly to the credit of Brahmagupta that he gave all integral solutions of the linear Diophantine equation, whereas Diophantus himself had been satisfied to give one particular solution of an indeterminate equation. Inasmuch as Brahmagupta used some of the same examples as Diophantus, we see again the likelihood of Greek influence in India – or the possibility that they both made use of a common source, possibly from Babylonia. It is interesting to note also that the algebra of Brahmagupta, like that of Diophantus, was syncopated. Addition was indicated by juxtaposition, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, as in our fractional notation but without the bar. The operations of multiplication and evolution (the taking of roots), as well as unknown quantities, were represented by abbreviations of appropriate words.")
^ Robert Kaplan, "The Nothing That Is: A Natural History of Zero", Allen Lane/The Penguin Press, London, 1999
^ ""The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius." – Pierre-Simon Laplace". History.mcs.st-and.ac.uk. Retrieved 2014-06-24.
^ A.P. Juschkewitsch, "Geschichte der Mathematik im Mittelalter", Teubner, Leipzig, 1964
^ Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "The Arabic Hegemony" p. 230. (cf., "The six cases of equations given above exhaust all possibilities for linear and quadratic equations having positive root. So systematic and exhaustive was al-Khwārizmī's exposition that his readers must have had little difficulty in mastering the solutions.")
^ Gandz and Saloman (1936), The sources of Khwarizmi's algebra, Osiris i, pp. 263–77: "In a sense, Khwarizmi is more entitled to be called "the father of algebra" than Diophantus because Khwarizmi is the first to teach algebra in an elementary form and for its own sake, Diophantus is primarily concerned with the theory of numbers".
^ Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "The Arabic Hegemony" p. 229. (cf., "It is not certain just what the terms al-jabr and muqabalah mean, but the usual interpretation is similar to that implied in the translation above. The word al-jabr presumably meant something like "restoration" or "completion" and seems to refer to the transposition of subtracted terms to the other side of an equation; the word muqabalah is said to refer to "reduction" or "balancing" – that is, the cancellation of like terms on opposite sides of the equation.")
^ Rashed, R.; Armstrong, Angela (1994). The Development of Arabic Mathematics. Springer. pp. 11–12. ISBN 0-7923-2565-6. OCLC 29181926.
^ Victor J. Katz (1998). History of Mathematics: An Introduction, pp. 255–59. Addison-Wesley. ISBN 0-321-01618-1.
^ F. Woepcke (1853). Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi. Paris.
^ Katz, Victor J. (1995). "Ideas of Calculus in Islam and India". Mathematics Magazine. 68 (3): 163–74. doi:10.1080/0025570X.1995.11996307.
^ Kunitzsch, Paul (2003), "The Transmission of Hindu-Arabic Numerals Reconsidered", in J. P. Hogendijk; A. I. Sabra (eds.), The Enterprise of Science in Islam: New Perspectives, MIT Press, pp. 3–22 (12–13), ISBN 978-0-262-19482-2
^ Marie-Thérèse d'Alverny, "Translations and Translators", pp. 421–62 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
^ Guy Beaujouan, "The Transformation of the Quadrivium", pp. 463–87 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
^ O'Connor, John J.; Robertson, Edmund F., "al-Marrakushi ibn Al-Banna", MacTutor History of Mathematics archive, University of St Andrews.
^ Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. p. 298. ISBN 0-393-04002-X.
^ ^a ^b O'Connor, John J.; Robertson, Edmund F., "Abu'l Hasan ibn Ali al Qalasadi", MacTutor History of Mathematics archive, University of St Andrews.
^ Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "Revival and Decline of Greek Mathematics" p. 178 (cf., "The chief difference between Diophantine syncopation and the modern algebraic notation is the lack of special symbols for operations and relations, as well as of the exponential notation.")
^ Grant, Edward and John E. Murdoch (1987), eds., Mathematics and Its Applications to Science and Natural Philosophy in the Middle Ages, (Cambridge: Cambridge University Press) ISBN 0-521-32260-X.
^ Mathematical Magazine, Volume 1. Artemas Martin, 1887. Pg 124
^ Der Algorismus proportionum des Nicolaus Oresme: Zum ersten Male nach der Lesart der Handschrift R.40.2. der Königlichen Gymnasial-bibliothek zu Thorn. Nicole Oresme. S. Calvary & Company, 1868.
^ Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), pp. 332–45, 382–91.
^ Later early modern version: A New System of Mercantile Arithmetic: Adapted to the Commerce of the United States, in Its Domestic and Foreign Relations with Forms of Accounts and Other Writings Usually Occurring in Trade. By Michael Walsh. Edmund M. Blunt (proprietor.), 1801.
^ Miller, Jeff (4 June 2006). "Earliest Uses of Symbols of Operation". Gulf High School. Retrieved 24 September 2006.
^ Arithmetical Books from the Invention of Printing to the Present Time. By Augustus De Morgan. p 2.
^ Grattan-Guinness, Ivor (1997). The Rainbow of Mathematics: A History of the Mathematical Sciences. W.W. Norton. ISBN 0-393-32030-8.
^ Arithmetica integra. By Michael Stifel, Philipp Melanchton. Norimbergæ: Apud Iohan Petreium, 1544.
^ The History of Mathematics By Anne Roone. Pg 40
^ Memoirs of John Napier of Merchiston. By Mark Napier
^ An Account of the Life, Writings, and Inventions of John Napier, of Merchiston. By David Stewart Erskine Earl of Buchan, Walter Minto
^ Cajori, Florian (1919). A History of Mathematics. Macmillan. p. 157.
^ Jan Gullberg, Mathematics from the birth of numbers, W. W. Norton & Company; ISBN 978-0-393-04002-9. pg 963–965,
^ Synopsis Palmariorum Matheseos. By William Jones. 1706. (Alt: Synopsis Palmariorum Matheseos: or, a New Introduction to the Mathematics. archive.org.)
^ When Less is More: Visualizing Basic Inequalities. By Claudi Alsina, Roger B. Nelse. Pg 18.
^ Euler, Leonhard, Solutio problematis ad geometriam situs pertinentis
^ The elements of geometry. By William Emerson
^ The Doctrine of Proportion, Arithmetical and Geometrical. Together with a General Method of Arening by Proportional Quantities. By William Emerson.
^ The Mathematical Correspondent. By George Baron. 83
^ Vitulli, Marie. "A Brief History of Linear Algebra and Matrix Theory". Department of Mathematics. University of Oregon. Archived from the original on 2012-09-10. Retrieved 2012-01-24.
^ "Kramp biography". History.mcs.st-and.ac.uk. Retrieved 2014-06-24.
^ Mécanique analytique: Volume 1, Volume 2. By Joseph Louis Lagrange. Ms. Ve Courcier, 1811.
^ The collected mathematical papers of Arthur Cayley. Volume 11. Page 243.
^ Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1. By Ari Ben-Menahem. Pg 2070.
^ Vitulli, Marie. "A Brief History of Linear Algebra and Matrix Theory". Department of Mathematics. University of Oregon. Originally at: darkwing.uoregon.edu/~vitulli/441.sp04/LinAlgHistory.html
^ The Words of Mathematics. By Steven Schwartzman. 6.
^ Electro-Magnetism: Theory and Applications. By A. Pramanik. 38
^ History of Nabla and Other Math Symbols. homepages.math.uic.edu/~hanson.
^ Hamilton, William Rowan (1854–1855). Wilkins, David R. (ed.). "On some Extensions of Quaternions" (PDF). Philosophical Magazine (7–9): 492–499, 125–137, 261–269, 46–51, 280–290. ISSN 0302-7597.
^ "James Clerk Maxwell". IEEE Global History Network. Retrieved 25 March 2013.
^ Maxwell, James Clerk (1865). "A dynamical theory of the electromagnetic field" (PDF). Philosophical Transactions of the Royal Society of London. 155: 459–512. Bibcode:1865RSPT..155..459C. doi:10.1098/rstl.1865.0008. S2CID 186207827. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.)
^ Books I, II, III (1878) at the Internet Archive; Book IV (1887) at the Internet Archive
^ Cox, David A. (2012). Galois Theory. Pure and Applied Mathematics. Vol. 106 (2nd ed.). John Wiley & Sons. p. 348. ISBN 978-1118218426.
^ "TÜBİTAK ULAKBİM DergiPark". Journals.istanbul.edu.tr. Archived from the original on 2014-03-16. Retrieved 2014-06-24.
^ "Linear Algebra : Hussein Tevfik : Free Download & Streaming : Internet Archive". A.H. Boyajian. 1882. Retrieved 2014-06-24.
^ Ricci Curbastro, G. (1892). "Résumé de quelques travaux sur les systèmes variables de fonctions associés à une forme différentielle quadratique". Bulletin des Sciences Mathématiques. 2 (16): 167–189.
^ Voigt, Woldemar (1898). Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung. Leipzig: Von Veit.
^ Poincaré, Henri, "Analysis situs", Journal de l'École Polytechnique ser 2, 1 (1895) pp. 1–123
^ Whitehead, John B., Jr. (1901). "Review: Alternating Current Phenomena, by C. P. Steinmetz" (PDF). Bull. Amer. Math. Soc. 7 (9): 399–408. doi:10.1090/s0002-9904-1901-00825-7.{{cite journal}}: CS1 maint: multiple names: authors list (link)
^
There are many editions. Here are two:
- (French) Published 1901 by Gauthier-Villars, Paris. 230p. OpenLibrary OL15255022W, PDF.
- (Italian) Published 1960 by Edizione cremonese, Roma. 463p. OpenLibrary OL16587658M.
^ Ricci, Gregorio; Levi-Civita, Tullio (March 1900), "Méthodes de calcul différentiel absolu et leurs applications", Mathematische Annalen, 54 (1–2), Springer: 125–201, doi:10.1007/BF01454201, S2CID 120009332
^ Zermelo, Ernst (1904). "Beweis, dass jede Menge wohlgeordnet werden kann" (reprint). Mathematische Annalen. 59 (4): 514–16. doi:10.1007/BF01445300. S2CID 124189935.
^ On the Dynamics of the Electron (July) – via Wikisource.
^ Fréchet, Maurice, "Sur quelques points du calcul fonctionnel", PhD dissertation, 1906
^ Cuthbert Edmund Cullis (Author) (2011-06-05). "Matrices and determinoids Volume 2: Cuthbert Edmund Cullis: Amazon.com: Books". Retrieved 2014-06-24. {{cite web}}: |author= has generic name (help)
^ Can be assigned a given matrix: About a class of matrices. (Gr. Ueber eine Klasse von Matrizen: die sich einer gegebenen Matrix zuordnen lassen.) by Isay Schur
^ An Introduction To The Modern Theory Of Equations. By Florian Cajori.
^ Proceedings of the Prussian Academy of Sciences (1918). Pg 966.
^ Sitzungsberichte der Preussischen Akademie der Wissenschaften (1918) (Tr. Proceedings of the Prussian Academy of Sciences (1918)). archive.org; See also: Kaluza–Klein theory.
^ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 85–86, §3.5. ISBN 0-7167-0344-0.
^ R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
^ Schouten, Jan A. (1924). R. Courant (ed.). Der Ricci-Kalkül – Eine Einführung in die neueren Methoden und Probleme der mehrdimensionalen Differentialgeometrie (Ricci Calculus – An introduction in the latest methods and problems in multi-dimmensional differential geometry). Grundlehren der mathematischen Wissenschaften (in German). Vol. 10. Berlin: Springer Verlag.
^ Robert B. Ash. A Primer of Abstract Mathematics. Cambridge University Press, 1 Jan 1998
^ The New American Encyclopedic Dictionary. Edited by Edward Thomas Roe, Le Roy Hooker, Thomas W. Handford. Pg 34
^ The Mathematical Principles of Natural Philosophy, Volume 1. By Sir Isaac Newton, John Machin. Pg 12.
^ In The Scientific Outlook (1931)
^ Mathematics simplified and made attractive: or, The laws of motion explained. By Thomas Fisher. Pg 15. (cf. But an abstraction not founded upon, and not consonant with Nature and (Logical) Truth, would be a falsity, an insanity.)
^ Proposition VI, On Formally Undecidable Propositions in Principia Mathematica and Related Systems I (1931)
^ Casti, John L. 5 Golden Rules. New York: MJF Books, 1996.
^ Gr. Methoden Der Mathematischen Physik
^ P.A.M. Dirac (1927). "The Quantum Theory of the Emission and Absorption of Radiation". Proceedings of the Royal Society of London A. 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.
^ E. Fermi (1932). "Quantum Theory of Radiation". Reviews of Modern Physics. 4 (1): 87–132. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.
^ F. Bloch; A. Nordsieck (1937). "Note on the Radiation Field of the Electron". Physical Review. 52 (2): 54–59. Bibcode:1937PhRv...52...54B. doi:10.1103/PhysRev.52.54.
^ V. F. Weisskopf (1939). "On the Self-Energy and the Electromagnetic Field of the Electron". Physical Review. 56 (1): 72–85. Bibcode:1939PhRv...56...72W. doi:10.1103/PhysRev.56.72.
^ R. Oppenheimer (1930). "Note on the Theory of the Interaction of Field and Matter". Physical Review. 35 (5): 461–477. Bibcode:1930PhRv...35..461O. doi:10.1103/PhysRev.35.461.
^ Van der Waerden B.L. (1929). "Spinoranalyse". Nachr. Ges. Wiss. Göttingen Math.-Phys. 1929: 100–109.
^ Veblen O. (1933). "Geometry of two-component Spinors". Proc. Natl. Acad. Sci. USA. 19 (4): 462–474. Bibcode:1933PNAS...19..462V. doi:10.1073/pnas.19.4.462. PMC 1086023. PMID 16577541.
^ Dirac, P.A.M. (1939). "A new notation for quantum mechanics". Mathematical Proceedings of the Cambridge Philosophical Society. Vol. 35, no. 3. pp. 416–418. Bibcode:1939PCPS...35..416D. doi:10.1017/S0305004100021162.
^ H. Grassmann (1862). Extension Theory. History of Mathematics Sources. American Mathematical Society, London Mathematical Society, 2000 translation by Lloyd C. Kannenberg.
^ Weinberg, Steven (1964), The quantum theory of fields, Volume 2, Cambridge University Press, 1995, p. 358, ISBN 0-521-55001-7
^ "The Nobel Prize in Physics 1965". Nobel Foundation. Retrieved 2008-10-09.
^ S.L. Glashow (1961). "Partial-symmetries of weak interactions". Nuclear Physics. 22 (4): 579–588. Bibcode:1961NucPh..22..579G. doi:10.1016/0029-5582(61)90469-2.
^ S. Weinberg (1967). "A Model of Leptons". Physical Review Letters. 19 (21): 1264–1266. Bibcode:1967PhRvL..19.1264W. doi:10.1103/PhysRevLett.19.1264.
^ A. Salam (1968). N. Svartholm (ed.). Elementary Particle Physics: Relativistic Groups and Analyticity. Eighth Nobel Symposium. Stockholm: Almquvist and Wiksell. p. 367.
^ F. Englert; R. Brout (1964). "Broken Symmetry and the Mass of Gauge Vector Mesons". Physical Review Letters. 13 (9): 321–323. Bibcode:1964PhRvL..13..321E. doi:10.1103/PhysRevLett.13.321.
^ P.W. Higgs (1964). "Broken Symmetries and the Masses of Gauge Bosons". Physical Review Letters. 13 (16): 508–509. Bibcode:1964PhRvL..13..508H. doi:10.1103/PhysRevLett.13.508.
^ G.S. Guralnik; C.R. Hagen; T.W.B. Kibble (1964). "Global Conservation Laws and Massless Particles". Physical Review Letters. 13 (20): 585–587. Bibcode:1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585.
^ http://www.physics.drexel.edu/~vkasli/phys676/Notes%20for%20a%20brief%20history%20of%20quantum%20gravity%20-%20Carlo%20Rovelli.pdf
^ Bourbaki, Nicolas (1972). "Univers". In Artin, Michael; Grothendieck, Alexandre; Jean-Louis Verdier (eds.). Séminaire de Géométrie Algébrique du Bois Marie - 1963-64 - Théorie des topos et cohomologie étale des schémas - (SGA 4) - vol. 1 (Lecture notes in mathematics 269) (in French). Berlin; New York: Springer-Verlag. pp. 185–217.
^ F.J. Hasert; et al. (1973). "Search for elastic muon-neutrino electron scattering". Physics Letters B. 46 (1): 121. Bibcode:1973PhLB...46..121H. doi:10.1016/0370-2693(73)90494-2.
^ F.J. Hasert; et al. (1973). "Observation of neutrino-like interactions without muon or electron in the gargamelle neutrino experiment". Physics Letters B. 46 (1): 138. Bibcode:1973PhLB...46..138H. doi:10.1016/0370-2693(73)90499-1.
^ F.J. Hasert; et al. (1974). "Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment". Nuclear Physics B. 73 (1): 1. Bibcode:1974NuPhB..73....1H. doi:10.1016/0550-3213(74)90038-8.
^ D. Haidt (4 October 2004). "The discovery of the weak neutral currents". CERN Courier. Retrieved 2008-05-08.
^ "Mainpage".
^ Candelas, P. (1985). "Vacuum configurations for superstrings". Nuclear Physics B. 258: 46–74. Bibcode:1985NuPhB.258...46C. doi:10.1016/0550-3213(85)90602-9.
^ De Felice, F.; Clarke, C.J.S. (1990), Relativity on Curved Manifolds, p. 133
^ "Quantum invariants of knots and 3-manifolds" by V. G. Turaev (1994), page 71
^ Pisanski, Tomaž; Servatius, Brigitte (2013), "2.3.2 Cubic graphs and LCF notation", Configurations from a Graphical Viewpoint, Springer, p. 32, ISBN 9780817683641
^ Frucht, R. (1976), "A canonical representation of trivalent Hamiltonian graphs", Journal of Graph Theory, 1 (1): 45–60, doi:10.1002/jgt.3190010111
^ Fraleigh 2002:89; Hungerford 1997:230
^ Dehn, Edgar. Algebraic Equations, Dover. 1930:19
^ "The IBM 601 Multiplying Punch". Columbia.edu. Retrieved 2014-06-24.
^ "Interconnected Punched Card Equipment". Columbia.edu. 1935-10-24. Retrieved 2014-06-24.
^ Proceedings of the London Mathematical Society 42 (2)
^ Cook, Stephen (1971). "The complexity of theorem proving procedures". Proceedings of the Third Annual ACM Symposium on Theory of Computing. pp. 151–158.

External links

Mathematical Notation: Past and Future
History of Mathematical Notation
Earliest Uses of Mathematical Notation
Finger counting. files.chem.vt.edu.
Some Common Mathematical Symbols and Abbreviations (with History). Isaiah Lankham, Bruno Nachtergaele, Anne Schilling.

[7] Or the Middle Ages.

[9] Such characters, in fact, are preserved with little alteration in the Roman notation, an account of which may be found in John Leslie's Philosophy of Arithmetic.

[10] Number theory is branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well as the properties of objects made out of integers (e.g., rational numbers) or defined as generalizations of the integers (e.g., algebraic integers).

[17] Greek: μή μου τοὺς κύκλους τάραττε

[18] That is, $a^{2}+b^{2}=c^{2}$ .

[22] Magnitude (mathematics), the relative size of an object ; Magnitude (vector), a term for the size or length of a vector; Scalar (mathematics), a quantity defined only by its magnitude; Euclidean vector, a quantity defined by both its magnitude and its direction; Order of magnitude, the class of scale having a fixed value ratio to the preceding class.

[27] Autolycus' On the Moving Sphere is another ancient mathematical manuscript of the time.

[28] Proclus, a Greek mathematician who lived several centuries after Euclid, wrote in his commentary of the Elements: "Euclid, who put together the Elements, collecting many of Eudoxus' theorems, perfecting many of Theaetetus', and also bringing to irrefragable demonstration the things which were only somewhat loosely proved by his predecessors".

[37] The expression:
$2x^{4}+3x^{3}-4x^{2}+5x-6$
would be written as:
SS2 C3 x5 M S4 u6
.^{[citation needed]}

[40] such as the wheel and axle

[41] such as the rule, square, compasses, water level (reed level), and plumb-bob.

[44] The area of the square described on the hypotenuse of a right-angled triangle is equal to the sum of the areas of the squares described on the sides

[53] Al-Kindi also introduced cryptanalysis and frequency analysis.

[59] Something close to a proof by mathematical induction appears in a book written by Al-Karaji around 1000 AD, who used it to prove the binomial theorem, Pascal's triangle, and the sum of integral cubes.

[62] He thus came close to finding a general formula for the integrals of polynomials, but he was not concerned with any polynomials higher than the fourth degree.

[64] ut what he perceived as flaws in Euclid's Elements, especially the parallel postulate

[66] translated into Latin by Robert of Chester

[67] translated in various versions by Adelard of Bath, Herman of Carinthia, and Gerard of Cremona

[76] His own personal use started around 1351.

[81] Summa de Arithmetica: Geometria Proportioni et Proportionalita. Tr. Sum of Arithmetic: Geometry in proportions and proportionality.

[83] Much of the work originated from Piero della Francesca whom he appropriated and purloined.

[84] This was a special case of the methods given many centuries later by Ruffini and Horner.

[86] That is, ${\sqrt {~}}$ .

[87] Because, it is thought, it resembled a lowercase "r" (for "radix").

[89] Published in Description of the Marvelous Canon of Logarithms

[93] That is,
∷

[95] see Law of Continuity.

[96] Using Cartesian coordinates on the plane, the distance between two points (x₁, y₁) and (x₂, y₂) is defined by the formula:
$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}},$
which can be viewed as a version of the Pythagorean theorem.

[97] Further steps in abstraction were taken by Lobachevsky, Bolyai, Riemann, and Gauss who generalised the concepts of geometry to develop non-Euclidean geometries.

[98] Now called Pascal's triangle.

[99] For example, the "problem of points".

[100] That is, ${\infty }$ .

[101] For example, ${\frac {1}{\infty }}.$

[102] Original title, "De ratiociniis in ludo aleae"

[106] For example, the derivative of the function x would be written as ${\dot {x}}$ . The second derivative of x would be written as ${\ddot {x}}$ , etc.

[107] For example, the derivative of the function x with respect to the variable t in Leibniz's notation would be written as ${dx \over dt}$ .

[108] That is, $\int _{-N}^{N}f(x)\,dx$ .

[109] See also: List of representations of e

[110] Thus $f(x)$ denotes the mathematical result of the performance of the operation $f$ upon the subject $x$ . If upon this result the same operation were repeated, the new result would be expressed by $f[f(x)]$ , or more concisely by $f^{2}(x)$ , and so on. The quantity $x$ itself regarded as the result of the same operation $f$ upon some other function; the proper symbol for which is, by analogy, $f^{-1}(x)$ . Thus $f$ and $f^{-1}$ are symbols of inverse operations, the former cancelling the effect of the latter on the subject $x$ . $f(x)$ and $f^{-1}(x)$ in a similar manner are termed inverse functions.

[111] That is, $\Delta f(p)$

[112] That is, ${\sqrt {-1}}$

[113] Today, the symbol created by John Wallis, $\infty$ , is used for infinity.

[114] As in, $\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}$

[115] Capital-sigma notation uses a symbol that compactly represents summation of many similar terms: the summation symbol, Σ, an enlarged form of the upright capital Greek letter Sigma. This is defined as:

$\sum _{i=m}^{n}a_{i}=a_{m}+a_{m+1}+a_{m+2}+\cdots +a_{n-1}+a_{n}.$

Where, i represents the index of summation; a_i is an indexed variable representing each successive term in the series; m is the lower bound of summation, and n is the upper bound of summation. The "i = m" under the summation symbol means that the index i starts out equal to m. The index, i, is incremented by 1 for each successive term, stopping when i = n.

[116] That is, $n!=\int _{0}^{1}(-\ln s)^{n}\,{\rm {d}}s$ .
valid for n > 0.

[119] That is,
∝

[120] Proportionality is the ratio of one quantity to another, especially the ratio of a part compared to a whole. In a mathematical context, a proportion is the statement of equality between two ratios; See Proportionality (mathematics), the relationship of two variables whose ratio is constant. See also aspect ratio, geometric proportions.

[123] The curly d or Jacobi's delta.

[124] About the proof of Wilson's theorem. Disquisitiones Arithmeticae (1801) Article 76

[126] Galois theory and Galois geometry is named after him.

[128] That is, "subset of" and "superset of"; This would later be redeveloped by Ernst Schröder.

[129] A science of numbers that uses methods from mathematical analysis to solve problems about the integers.

[134] Quoted in Robert Perceval Graves' Life of Sir William Rowan Hamilton (3 volumes, 1882, 1885, 1889)

[135] That is, $\nabla$ (or, later called del, ∇)

[139] See Hamiltonian (quantum mechanics).

[140] That is, $i^{2}=j^{2}=k^{2}=ijk=-1$

[142] Though his use describes something different from what is now meant by a tensor. Namely, the norm operation in a certain type of algebraic system (now known as a Clifford algebra).

[143] That is,
$t=w+xi+yj+zk,\quad w,x,y,z\in \mathbb {R}$
where
$ij=ji=k,\quad i^{2}=-1,\quad j^{2}=+1.$

[144] This is Latin for "womb".

[148] That is, $q=w+xi+yj+zk$

[149] Clifford intersected algebra with Hamilton's quaternions by replacing Hermann Grassmann's rule e_pe_p = 0 by the rule e_pe_p = 1. For more details, see exterior algebra.

[150] See: Phasor, Group (mathematics), Signal velocity, Polyphase system, Harmonic oscillator, and RLC series circuit

[151] Or the concept of a fourth spatial dimension. See also: Spacetime, the unification of time and space as a four-dimensional continuum; and, Minkowski space, the mathematical setting for special relativity.

[155] See also: Mathematic fields and Field extension

[160] Comment after the proof that 1+1=2, completed in Principia mathematica, by Alfred North Whitehead ... and Bertrand Russell. Volume II, 1st edition (1912)

[162] This raises questions of the pure existence theorems.

[163] Peano's Formulario Mathematico, though less popular than Russell's work, continued through five editions. The fifth appeared in 1908 and included 4200 formulas and theorems.

[165] Inventor of set theory

[166] Transfinite arithmetic is the generalization of elementary arithmetic to infinite quantities like infinite sets; See Transfinite numbers, Transfinite induction, and Transfinite interpolation. See also Ordinal arithmetic.

[173] Such as Max Dehn, J. W. Alexander, and others.

[174] Such as the Alexander polynomial.

[175] (German: Algebraische Theorie der Körper)

[176] In this paper Steinitz axiomatically studied the properties of fields and defined many important field theoretic concepts like prime field, perfect field and the transcendence degree of a field extension.

[177] The indices range over set ${1, 2, 3$ },
$y=\sum _{i=1}^{3}c_{i}x^{i}=c_{1}x^{1}+c_{2}x^{2}+c_{3}x^{3}$
is reduced by the convention to:
$y=c_{i}x^{i}\,.$
Upper indices are not exponents but are indices of coordinates, coefficients or basis vectors.
See also: Ricci calculus

[180] Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields. See also: Synge J.L.; Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. pp. 6–108.

[189] Here a logical constant is a symbol in symbolic logic that has the same meaning in all models, such as the symbol "=" for "equals".
A constant, in a mathematical context, is a number that arises naturally in mathematics, such as π or e; Such mathematics constant value do not change. It can mean polynomial constant term (the term of degree 0) or the constant of integration, a free parameter arising in integration.
Related, the physical constant are a physical quantity generally believed to be universal and unchanging. Programming constants are a values that, unlike a variable, cannot be reassociated with a different value.

[190] Though not an index term, keywords are terms that represent information. A keyword is a word with special meaning (this is a semantic definition), while syntactically these are terminal symbols in the phrase grammar. See reserved word for the related concept.

[191] Most of these symbols can be found in propositional calculus, a formal system described as ${\mathcal {L}}={\mathcal {L}}\ (\mathrm {A} ,\ \Omega ,\ \mathrm {Z} ,\ \mathrm {I} )$ . $\mathrm {A}$ is the set of elements, such as the a in the example with Boolean algebra above. $\Omega$ is the set that contains the subsets that contain operations, such as $\lor$ or $\land$ . $\mathrm {Z}$ contains the inference rules, which are the rules dictating how inferences may be logically made, and $\mathrm {I}$ contains the axioms. See also: Basic and Derived Argument Forms.

[192] Usually denoted by x, y, z, or other lowercase letters
Here a symbols that represents a quantity in a mathematical expression, a mathematical variable as used in many sciences.
Variables can be symbolic name associated with a value and whose associated value may be changed, known in computer science as a variable reference. A variable can also be the operationalized way in which the attribute is represented for further data processing (e.g., a logical set of attributes). See also: Dependent and independent variables in statistics.

[193] Usually denoted by an uppercase letter followed by a list of variables, such as P(x) or Q(y,z)
Here a mathematical logic predicate, a fundamental concept in first-order logic. Grammatical predicates are grammatical components of a sentence.
Related is the syntactic predicate in parser technology which are guidelines for the parser process. In computer programming, a branch predication allows a choice to execute or not to execute a given instruction based on the content of a machine register.

[194] Representing ALL and EXISTS

[195] .g. ∃ for "there exists" and ∀ for "for all"

[196] See also: Dialetheism, Contradiction, and Paradox

[197] Related, facetious abstract nonsense describes certain kinds of arguments and methods related to category theory which resembles comical literary non-sequitur devices (not illogical non-sequiturs).

[199] Gödel's incompleteness theorems shows that Hilbert's program to find a complete and consistent set of axioms for all mathematics is impossible, giving a contested negative answer to Hilbert's second problem

[201] For example, take the statement "There exists a number x such that it is not y". Using the symbols of propositional calculus, this would become: $(\exists x)(x=\lnot y)$ .
If the Gödel numbers replace the symbols, it becomes: $\{8,4,11,9,8,11,5,1,13,9\}$ .
There are ten numbers, so the ten prime numbers are found and these are: $\{2,3,5,7,11,13,17,19,23,29\}$ .
Then, the Gödel numbers are made the powers of the respective primes and multiplied, giving: $2^{8}\times 3^{4}\times 5^{11}\times 7^{9}\times 11^{8}\times 13^{11}\times 17^{5}\times 19^{1}\times 23^{13}\times 29^{9}$ .
The resulting number is approximately $3.096262735\times 10^{78}$ .

[203] The Klein–Gordon equation is:

${\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\psi -\nabla ^{2}\psi +{\frac {m^{2}c^{2}}{\hbar ^{2}}}\psi =0.$

[205] The Dirac equation in the form originally proposed by Dirac is:

$\left(\beta mc^{2}+\sum _{k=1}^{3}\alpha _{k}p_{k}\,c\right)\psi (\mathbf {x} ,t)=i\hbar {\frac {\partial \psi (\mathbf {x} ,t)}{\partial t}}$

where, $ψ = ψ(x, t)$ is the wave function for the electron, $x$ and $t$ are the space and time coordinates, $m$ is the rest mass of the electron, $p$ is the momentum, understood to be the momentum operator in the Schrödinger theory, $c$ is the speed of light, and $ħ = h /2 π$ is the reduced Planck constant.

[207] That is,

$\partial _{\mu }(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu })+\left({\frac {mc}{\hbar }}\right)^{2}A^{\nu }=0$

[211] The theorem applies more generally to any sufficiently strong formal system, showing that truth in the standard model of the system cannot be defined within the system.

[212] Named to honor Voigt's 1898 work.

[213] Named after Arthur Moritz Schoenflies

[216] See Galois connections.

[217] Oystein Ore would also write "Number Theory and Its History".

[218] $\langle \phi |\psi \rangle$

[222] That the scattering amplitude can be thought of as an analytic function of the angular momentum, and that the position of the poles determine power-law growth rates of the amplitude in the purely mathematical region of large values of the cosine of the scattering angle.

[223] That is, $\scriptstyle \Box$

[224] Also known as the d'Alembertian or wave operator.

[225] Also known as, "permutation symbol" (see: permutation), "antisymmetric symbol" (see: antisymmetric), or "alternating symbol"

[227] Note that "masses" (e.g., the coherent non-definite body shape) of particles are periodically reevaluated by the scientific community. The values may have been adjusted; adjustment by operations carried out on instruments in order that it provides given indications corresponding to given values of the measurand. In engineering, mathematics, and geodesy, the optimal parameter such estimation of a mathematical model so as to best fit a data set.

[228] For the consensus, see Particle Data Group.

[243] A locally defined set of four linearly independent vector fields called a tetrad

[246] His usage of the Einstein summation was in order to offset the inconvenience in describing contractions and covariant differentiation in modern abstract tensor notation, while maintaining explicit covariance of the expressions involved.

[247] See also: String theory landscape and Swampland

[248] Devised by Joshua Lederberg and extended by Coxeter and Frucht

[256] And, in 1938, Turing, A. M. (1938). "On Computable Numbers, with an Application to the Entscheidungsproblem. A Correction". Proceedings of the London Mathematical Society. s2-43: 544–546. doi:10.1112/plms/s2-43.6.544..

[257] Among von Neumann's other contributions include the application of operator theory to quantum mechanics, in the development of functional analysis, and on various forms of operator theory.

[1] Florian Cajori. A History of Mathematical Notations: Two Volumes in One. Cosimo, Inc., Dec 1, 2011

[2] A Dictionary of Science, Literature, & Art, Volume 2. Edited by William Thomas Brande, George William Cox. Pg 683

[3] "Notation - from Wolfram MathWorld". Mathworld.wolfram.com. Retrieved 2014-06-24.

[4] Diophantos of Alexandria: A Study in the History of Greek Algebra. By Sir Thomas Little Heath. Pg 77.

[5] Mathematics: Its Power and Utility. By Karl J. Smith. Pg 86.

[6] The Commercial Revolution and the Beginnings of Western Mathematics in Renaissance Florence, 1300–1500. Warren Van Egmond. 1976. Page 233.

[8] Solomon Gandz. "The Sources of al-Khowarizmi's Algebra"

[11] Encyclopædia Americana. By Thomas Gamaliel Bradford. Pg 314

[12] Mathematical Excursion, Enhanced Edition: Enhanced Webassign Edition By Richard N. Aufmann, Joanne Lockwood, Richard D. Nation, Daniel K. Cleg. Pg 186

[13] Mathematics in Egypt and Mesopotamia^{[dead link]}

[14] Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "Mesopotamia" p. 25.

[15] Duncan J. Melville (2003). Third Millennium Chronology, Third Millennium Mathematics. St. Lawrence University.

[16] Aaboe, Asger (1998). Episodes from the Early History of Mathematics. New York: Random House. pp. 30–31.

[19] Heath. A Manual of Greek Mathematics. p. 5.

[20] Sir Thomas L. Heath, A Manual of Greek Mathematics, Dover, 1963, p. 1: "In the case of mathematics, it is the Greek contribution which it is most essential to know, for it was the Greeks who made mathematics a science."

[Encyclopaedia_Perthensi-21] The new encyclopædia; or, Universal dictionary of arts and sciences. By Encyclopaedia Perthensi. Pg 49

[23] Calinger, Ronald (1999). A Contextual History of Mathematics. Prentice-Hall. p. 150. ISBN 0-02-318285-7. Shortly after Euclid, compiler of the definitive textbook, came Archimedes of Syracuse (ca. 287 212 BC), the most original and profound mathematician of antiquity.

[24] "Archimedes of Syracuse". The MacTutor History of Mathematics archive. January 1999. Retrieved 2008-06-09.

[25] O'Connor, J.J.; Robertson, E.F. (February 1996). "A history of calculus". University of St Andrews. Archived from the original on 15 July 2007. Retrieved 2007-08-07. {{cite web}}: Unknown parameter |deadurl= ignored (|url-status= suggested) (help)

[26] "Proclus' Summary". Gap.dcs.st-and.ac.uk. Archived from the original on 23 September 2015. Retrieved 24 June 2014. {{cite web}}: Unknown parameter |dead-url= ignored (|url-status= suggested) (help)

[29] Caldwell, John (1981) "The De Institutione Arithmetica and the De Institutione Musica", pp. 135–54 in Margaret Gibson, ed., Boethius: His Life, Thought, and Influence, (Oxford: Basil Blackwell).

[30] Folkerts, Menso, "Boethius" Geometrie II, (Wiesbaden: Franz Steiner Verlag, 1970).

[31] Mathematics and Measurement By Oswald Ashton Wentworth Dilk. Pg 14

[books.google.com-32] A dictionary of science, literature and art, ed. by W.T. Brande. Pg 683

[Boyer-33] Boyer, Carl B. A History of Mathematics, 2nd edition, John Wiley & Sons, Inc., 1991.

[34] Diophantine Equations. Submitted by: Aaron Zerhusen, Chris Rakes, & Shasta Meece. MA 330-002. Dr. Carl Eberhart. February 16, 1999.

[35] A History of Greek Mathematics: From Aristarchus to Diophantus. By Sir Thomas Little Heath. Pg 456

[36] A History of Greek Mathematics: From Aristarchus to Diophantus. By Sir Thomas Little Heath. Pg 458

[38] The American Mathematical Monthly, Volume 16. Pg 131

[39] "Overview of Chinese mathematics". Groups.dcs.st-and.ac.uk. Retrieved 2014-06-24.

[42] George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Penguin Books, London, 1991, pp.140—148

[43] Georges Ifrah, Universalgeschichte der Zahlen, Campus, Frankfurt/New York, 1986, pp.428—437

[45] "Frank J. Swetz and T. I. Kao: Was Pythagoras Chinese?". Psupress.psu.edu. Retrieved 2014-06-24.

[needham_volume_3_109-46] Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd..

[restivo_32-47] Sal Restivo

[needham_volume_3_109_2-48] Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.

[gauchet_151-49] Marcel Gauchet, 151.

[Boyer_Brahmagupta_Indeterminate_equations-50] Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "China and India" p. 221. (cf., "he was the first one to give a general solution of the linear Diophantine equation ax + by = c, where a, b, and c are integers. [...] It is greatly to the credit of Brahmagupta that he gave all integral solutions of the linear Diophantine equation, whereas Diophantus himself had been satisfied to give one particular solution of an indeterminate equation. Inasmuch as Brahmagupta used some of the same examples as Diophantus, we see again the likelihood of Greek influence in India – or the possibility that they both made use of a common source, possibly from Babylonia. It is interesting to note also that the algebra of Brahmagupta, like that of Diophantus, was syncopated. Addition was indicated by juxtaposition, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, as in our fractional notation but without the bar. The operations of multiplication and evolution (the taking of roots), as well as unknown quantities, were represented by abbreviations of appropriate words.")

[51] Robert Kaplan, "The Nothing That Is: A Natural History of Zero", Allen Lane/The Penguin Press, London, 1999

[52] ""The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius." – Pierre-Simon Laplace". History.mcs.st-and.ac.uk. Retrieved 2014-06-24.

[54] A.P. Juschkewitsch, "Geschichte der Mathematik im Mittelalter", Teubner, Leipzig, 1964

[55] Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "The Arabic Hegemony" p. 230. (cf., "The six cases of equations given above exhaust all possibilities for linear and quadratic equations having positive root. So systematic and exhaustive was al-Khwārizmī's exposition that his readers must have had little difficulty in mastering the solutions.")

[56] Gandz and Saloman (1936), The sources of Khwarizmi's algebra, Osiris i, pp. 263–77: "In a sense, Khwarizmi is more entitled to be called "the father of algebra" than Diophantus because Khwarizmi is the first to teach algebra in an elementary form and for its own sake, Diophantus is primarily concerned with the theory of numbers".

[Boyer-229-57] Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "The Arabic Hegemony" p. 229. (cf., "It is not certain just what the terms al-jabr and muqabalah mean, but the usual interpretation is similar to that implied in the translation above. The word al-jabr presumably meant something like "restoration" or "completion" and seems to refer to the transposition of subtracted terms to the other side of an equation; the word muqabalah is said to refer to "reduction" or "balancing" – that is, the cancellation of like terms on opposite sides of the equation.")

[Rashed-Armstrong-58] Rashed, R.; Armstrong, Angela (1994). The Development of Arabic Mathematics. Springer. pp. 11–12. ISBN 0-7923-2565-6. OCLC 29181926.

[60] Victor J. Katz (1998). History of Mathematics: An Introduction, pp. 255–59. Addison-Wesley. ISBN 0-321-01618-1.

[61] F. Woepcke (1853). Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi. Paris.

[Katz-63] Katz, Victor J. (1995). "Ideas of Calculus in Islam and India". Mathematics Magazine. 68 (3): 163–74. doi:10.1080/0025570X.1995.11996307.

[65] Kunitzsch, Paul (2003), "The Transmission of Hindu-Arabic Numerals Reconsidered", in J. P. Hogendijk; A. I. Sabra (eds.), The Enterprise of Science in Islam: New Perspectives, MIT Press, pp. 3–22 (12–13), ISBN 978-0-262-19482-2

[68] Marie-Thérèse d'Alverny, "Translations and Translators", pp. 421–62 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).

[69] Guy Beaujouan, "The Transformation of the Quadrivium", pp. 463–87 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).

[70] O'Connor, John J.; Robertson, Edmund F., "al-Marrakushi ibn Al-Banna", MacTutor History of Mathematics archive, University of St Andrews.

[Gullberg-71] Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. p. 298. ISBN 0-393-04002-X.

[Qalasadi-72] O'Connor, John J.; Robertson, Edmund F., "Abu'l Hasan ibn Ali al Qalasadi", MacTutor History of Mathematics archive, University of St Andrews.

[73] Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "Revival and Decline of Greek Mathematics" p. 178 (cf., "The chief difference between Diophantine syncopation and the modern algebraic notation is the lack of special symbols for operations and relations, as well as of the exponential notation.")

[74] Grant, Edward and John E. Murdoch (1987), eds., Mathematics and Its Applications to Science and Natural Philosophy in the Middle Ages, (Cambridge: Cambridge University Press) ISBN 0-521-32260-X.

[75] Mathematical Magazine, Volume 1. Artemas Martin, 1887. Pg 124

[77] Der Algorismus proportionum des Nicolaus Oresme: Zum ersten Male nach der Lesart der Handschrift R.40.2. der Königlichen Gymnasial-bibliothek zu Thorn. Nicole Oresme. S. Calvary & Company, 1868.

[78] Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), pp. 332–45, 382–91.

[79] Later early modern version: A New System of Mercantile Arithmetic: Adapted to the Commerce of the United States, in Its Domestic and Foreign Relations with Forms of Accounts and Other Writings Usually Occurring in Trade. By Michael Walsh. Edmund M. Blunt (proprietor.), 1801.

[80] Miller, Jeff (4 June 2006). "Earliest Uses of Symbols of Operation". Gulf High School. Retrieved 24 September 2006.

[82] Arithmetical Books from the Invention of Printing to the Present Time. By Augustus De Morgan. p 2.

[85] Grattan-Guinness, Ivor (1997). The Rainbow of Mathematics: A History of the Mathematical Sciences. W.W. Norton. ISBN 0-393-32030-8.

[88] Arithmetica integra. By Michael Stifel, Philipp Melanchton. Norimbergæ: Apud Iohan Petreium, 1544.

[90] The History of Mathematics By Anne Roone. Pg 40

[91] Memoirs of John Napier of Merchiston. By Mark Napier

[92] An Account of the Life, Writings, and Inventions of John Napier, of Merchiston. By David Stewart Erskine Earl of Buchan, Walter Minto

[94] Cajori, Florian (1919). A History of Mathematics. Macmillan. p. 157.

[103] Jan Gullberg, Mathematics from the birth of numbers, W. W. Norton & Company; ISBN 978-0-393-04002-9. pg 963–965,

[104] Synopsis Palmariorum Matheseos. By William Jones. 1706. (Alt: Synopsis Palmariorum Matheseos: or, a New Introduction to the Mathematics. archive.org.)

[105] When Less is More: Visualizing Basic Inequalities. By Claudi Alsina, Roger B. Nelse. Pg 18.

[117] Euler, Leonhard, Solutio problematis ad geometriam situs pertinentis

[118] The elements of geometry. By William Emerson

[121] The Doctrine of Proportion, Arithmetical and Geometrical. Together with a General Method of Arening by Proportional Quantities. By William Emerson.

[122] The Mathematical Correspondent. By George Baron. 83

[125] Vitulli, Marie. "A Brief History of Linear Algebra and Matrix Theory". Department of Mathematics. University of Oregon. Archived from the original on 2012-09-10. Retrieved 2012-01-24.

[127] "Kramp biography". History.mcs.st-and.ac.uk. Retrieved 2014-06-24.

[130] Mécanique analytique: Volume 1, Volume 2. By Joseph Louis Lagrange. Ms. Ve Courcier, 1811.

[131] The collected mathematical papers of Arthur Cayley. Volume 11. Page 243.

[132] Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1. By Ari Ben-Menahem. Pg 2070.

[Vitulli,_Marie-133] Vitulli, Marie. "A Brief History of Linear Algebra and Matrix Theory". Department of Mathematics. University of Oregon. Originally at: darkwing.uoregon.edu/~vitulli/441.sp04/LinAlgHistory.html

[136] The Words of Mathematics. By Steven Schwartzman. 6.

[137] Electro-Magnetism: Theory and Applications. By A. Pramanik. 38

[138] History of Nabla and Other Math Symbols. homepages.math.uic.edu/~hanson.

[141] Hamilton, William Rowan (1854–1855). Wilkins, David R. (ed.). "On some Extensions of Quaternions" (PDF). Philosophical Magazine (7–9): 492–499, 125–137, 261–269, 46–51, 280–290. ISSN 0302-7597.

[145] "James Clerk Maxwell". IEEE Global History Network. Retrieved 25 March 2013.

[ADTEF-146] Maxwell, James Clerk (1865). "A dynamical theory of the electromagnetic field" (PDF). Philosophical Transactions of the Royal Society of London. 155: 459–512. Bibcode:1865RSPT..155..459C. doi:10.1098/rstl.1865.0008. S2CID 186207827. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.)

[147] Books I, II, III (1878) at the Internet Archive; Book IV (1887) at the Internet Archive

[152] Cox, David A. (2012). Galois Theory. Pure and Applied Mathematics. Vol. 106 (2nd ed.). John Wiley & Sons. p. 348. ISBN 978-1118218426.

[153] "TÜBİTAK ULAKBİM DergiPark". Journals.istanbul.edu.tr. Archived from the original on 2014-03-16. Retrieved 2014-06-24.

[154] "Linear Algebra : Hussein Tevfik : Free Download & Streaming : Internet Archive". A.H. Boyajian. 1882. Retrieved 2014-06-24.

[156] Ricci Curbastro, G. (1892). "Résumé de quelques travaux sur les systèmes variables de fonctions associés à une forme différentielle quadratique". Bulletin des Sciences Mathématiques. 2 (16): 167–189.

[157] Voigt, Woldemar (1898). Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung. Leipzig: Von Veit.

[158] Poincaré, Henri, "Analysis situs", Journal de l'École Polytechnique ser 2, 1 (1895) pp. 1–123

[159] Whitehead, John B., Jr. (1901). "Review: Alternating Current Phenomena, by C. P. Steinmetz" (PDF). Bull. Amer. Math. Soc. 7 (9): 399–408. doi:10.1090/s0002-9904-1901-00825-7.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[161] There are many editions. Here are two:
(French) Published 1901 by Gauthier-Villars, Paris. 230p. OpenLibrary OL15255022W, PDF.

(Italian) Published 1960 by Edizione cremonese, Roma. 463p. OpenLibrary OL16587658M.

[204] (French) Published 1901 by Gauthier-Villars, Paris. 230p. OpenLibrary OL15255022W, PDF.

[205] (Italian) Published 1960 by Edizione cremonese, Roma. 463p. OpenLibrary OL16587658M.

[164] Ricci, Gregorio; Levi-Civita, Tullio (March 1900), "Méthodes de calcul différentiel absolu et leurs applications", Mathematische Annalen, 54 (1–2), Springer: 125–201, doi:10.1007/BF01454201, S2CID 120009332

[Zermelo,_1904-167] Zermelo, Ernst (1904). "Beweis, dass jede Menge wohlgeordnet werden kann" (reprint). Mathematische Annalen. 59 (4): 514–16. doi:10.1007/BF01445300. S2CID 124189935.

[168] On the Dynamics of the Electron (July) – via Wikisource.

[169] Fréchet, Maurice, "Sur quelques points du calcul fonctionnel", PhD dissertation, 1906

[170] Cuthbert Edmund Cullis (Author) (2011-06-05). "Matrices and determinoids Volume 2: Cuthbert Edmund Cullis: Amazon.com: Books". Retrieved 2014-06-24. {{cite web}}: |author= has generic name (help)

[171] Can be assigned a given matrix: About a class of matrices. (Gr. Ueber eine Klasse von Matrizen: die sich einer gegebenen Matrix zuordnen lassen.) by Isay Schur

[172] An Introduction To The Modern Theory Of Equations. By Florian Cajori.

[178] Proceedings of the Prussian Academy of Sciences (1918). Pg 966.

[179] Sitzungsberichte der Preussischen Akademie der Wissenschaften (1918) (Tr. Proceedings of the Prussian Academy of Sciences (1918)). archive.org; See also: Kaluza–Klein theory.

[181] J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 85–86, §3.5. ISBN 0-7167-0344-0.

[182] R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.

[183] Schouten, Jan A. (1924). R. Courant (ed.). Der Ricci-Kalkül – Eine Einführung in die neueren Methoden und Probleme der mehrdimensionalen Differentialgeometrie (Ricci Calculus – An introduction in the latest methods and problems in multi-dimmensional differential geometry). Grundlehren der mathematischen Wissenschaften (in German). Vol. 10. Berlin: Springer Verlag.

[184] Robert B. Ash. A Primer of Abstract Mathematics. Cambridge University Press, 1 Jan 1998

[185] The New American Encyclopedic Dictionary. Edited by Edward Thomas Roe, Le Roy Hooker, Thomas W. Handford. Pg 34

[186] The Mathematical Principles of Natural Philosophy, Volume 1. By Sir Isaac Newton, John Machin. Pg 12.

[187] In The Scientific Outlook (1931)

[188] Mathematics simplified and made attractive: or, The laws of motion explained. By Thomas Fisher. Pg 15. (cf. But an abstraction not founded upon, and not consonant with Nature and (Logical) Truth, would be a falsity, an insanity.)

[198] Proposition VI, On Formally Undecidable Propositions in Principia Mathematica and Related Systems I (1931)

[200] Casti, John L. 5 Golden Rules. New York: MJF Books, 1996.

[202] Gr. Methoden Der Mathematischen Physik

[dirac-204] P.A.M. Dirac (1927). "The Quantum Theory of the Emission and Absorption of Radiation". Proceedings of the Royal Society of London A. 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.

[fermi-206] E. Fermi (1932). "Quantum Theory of Radiation". Reviews of Modern Physics. 4 (1): 87–132. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.

[bloch-208] F. Bloch; A. Nordsieck (1937). "Note on the Radiation Field of the Electron". Physical Review. 52 (2): 54–59. Bibcode:1937PhRv...52...54B. doi:10.1103/PhysRev.52.54.

[weisskopf-209] V. F. Weisskopf (1939). "On the Self-Energy and the Electromagnetic Field of the Electron". Physical Review. 56 (1): 72–85. Bibcode:1939PhRv...56...72W. doi:10.1103/PhysRev.56.72.

[oppenheimer-210] R. Oppenheimer (1930). "Note on the Theory of the Interaction of Field and Matter". Physical Review. 35 (5): 461–477. Bibcode:1930PhRv...35..461O. doi:10.1103/PhysRev.35.461.

[214] Van der Waerden B.L. (1929). "Spinoranalyse". Nachr. Ges. Wiss. Göttingen Math.-Phys. 1929: 100–109.

[215] Veblen O. (1933). "Geometry of two-component Spinors". Proc. Natl. Acad. Sci. USA. 19 (4): 462–474. Bibcode:1933PNAS...19..462V. doi:10.1073/pnas.19.4.462. PMC 1086023. PMID 16577541.

[Dirac-219] Dirac, P.A.M. (1939). "A new notation for quantum mechanics". Mathematical Proceedings of the Cambridge Philosophical Society. Vol. 35, no. 3. pp. 416–418. Bibcode:1939PCPS...35..416D. doi:10.1017/S0305004100021162.

[Grassmann-220] H. Grassmann (1862). Extension Theory. History of Mathematics Sources. American Mathematical Society, London Mathematical Society, 2000 translation by Lloyd C. Kannenberg.

[221] Weinberg, Steven (1964), The quantum theory of fields, Volume 2, Cambridge University Press, 1995, p. 358, ISBN 0-521-55001-7

[nobel65-226] "The Nobel Prize in Physics 1965". Nobel Foundation. Retrieved 2008-10-09.

[229] S.L. Glashow (1961). "Partial-symmetries of weak interactions". Nuclear Physics. 22 (4): 579–588. Bibcode:1961NucPh..22..579G. doi:10.1016/0029-5582(61)90469-2.

[230] S. Weinberg (1967). "A Model of Leptons". Physical Review Letters. 19 (21): 1264–1266. Bibcode:1967PhRvL..19.1264W. doi:10.1103/PhysRevLett.19.1264.

[231] A. Salam (1968). N. Svartholm (ed.). Elementary Particle Physics: Relativistic Groups and Analyticity. Eighth Nobel Symposium. Stockholm: Almquvist and Wiksell. p. 367.

[232] F. Englert; R. Brout (1964). "Broken Symmetry and the Mass of Gauge Vector Mesons". Physical Review Letters. 13 (9): 321–323. Bibcode:1964PhRvL..13..321E. doi:10.1103/PhysRevLett.13.321.

[233] P.W. Higgs (1964). "Broken Symmetries and the Masses of Gauge Bosons". Physical Review Letters. 13 (16): 508–509. Bibcode:1964PhRvL..13..508H. doi:10.1103/PhysRevLett.13.508.

[234] G.S. Guralnik; C.R. Hagen; T.W.B. Kibble (1964). "Global Conservation Laws and Massless Particles". Physical Review Letters. 13 (20): 585–587. Bibcode:1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585.

[235] ttp://www.physics.drexel.edu/~vkasli/phys676/Notes%20for%20a%20brief%20history%20of%20quantum%20gravity%20-%20Carlo%20Rovelli.pdf

[236] Bourbaki, Nicolas (1972). "Univers". In Artin, Michael; Grothendieck, Alexandre; Jean-Louis Verdier (eds.). Séminaire de Géométrie Algébrique du Bois Marie - 1963-64 - Théorie des topos et cohomologie étale des schémas - (SGA 4) - vol. 1 (Lecture notes in mathematics 269) (in French). Berlin; New York: Springer-Verlag. pp. 185–217.

[237] F.J. Hasert; et al. (1973). "Search for elastic muon-neutrino electron scattering". Physics Letters B. 46 (1): 121. Bibcode:1973PhLB...46..121H. doi:10.1016/0370-2693(73)90494-2.

[238] F.J. Hasert; et al. (1973). "Observation of neutrino-like interactions without muon or electron in the gargamelle neutrino experiment". Physics Letters B. 46 (1): 138. Bibcode:1973PhLB...46..138H. doi:10.1016/0370-2693(73)90499-1.

[239] F.J. Hasert; et al. (1974). "Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment". Nuclear Physics B. 73 (1): 1. Bibcode:1974NuPhB..73....1H. doi:10.1016/0550-3213(74)90038-8.

[240] D. Haidt (4 October 2004). "The discovery of the weak neutral currents". CERN Courier. Retrieved 2008-05-08.

[241] "Mainpage".

[242] Candelas, P. (1985). "Vacuum configurations for superstrings". Nuclear Physics B. 258: 46–74. Bibcode:1985NuPhB.258...46C. doi:10.1016/0550-3213(85)90602-9.

[244] De Felice, F.; Clarke, C.J.S. (1990), Relativity on Curved Manifolds, p. 133

[245] "Quantum invariants of knots and 3-manifolds" by V. G. Turaev (1994), page 71

[249] Pisanski, Tomaž; Servatius, Brigitte (2013), "2.3.2 Cubic graphs and LCF notation", Configurations from a Graphical Viewpoint, Springer, p. 32, ISBN 9780817683641

[250] Frucht, R. (1976), "A canonical representation of trivalent Hamiltonian graphs", Journal of Graph Theory, 1 (1): 45–60, doi:10.1002/jgt.3190010111

[251] Fraleigh 2002:89; Hungerford 1997:230

[252] Dehn, Edgar. Algebraic Equations, Dover. 1930:19

[253] "The IBM 601 Multiplying Punch". Columbia.edu. Retrieved 2014-06-24.

[254] "Interconnected Punched Card Equipment". Columbia.edu. 1935-10-24. Retrieved 2014-06-24.

[255] Proceedings of the London Mathematical Society 42 (2)

[258] Cook, Stephen (1971). "The complexity of theorem proving procedures". Proceedings of the Third Annual ACM Symposium on Theory of Computing. pp. 151–158.

[1]

[2]

[3]

[4]

[5]

[6]

[note 1]

[7]

[note 2]

[note 3]

[8]

[9]

[10]

[11]

[12]

[13]

[note 4]

[note 5]

[14]

[15]

[16]

[note 6]

[17]

[18]

[19]

[20]

[note 7]

[note 8]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[note 9]

[29]

[30]

[note 10]

[note 11]

[31]

[32]

[note 12]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[note 13]

[41]

[42]

[43]

[44]

[45]

[note 14]

[46]

[47]

[note 15]

[48]

[note 16]

[49]

[note 17]

[note 18]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[note 19]

[58]

[59]

[60]

[61]

[note 20]

[62]

[note 21]

[note 22]

[63]

[note 23]

[note 24]

[64]

[note 25]

[65]

[66]

[67]

[note 26]

[68]

[note 27]

[note 28]

[note 29]

[note 30]

[note 31]

[note 32]